 |
Главная |
Моменты случайных величин
|
из
5.00
|
Наряду с рассмотренными числовыми характеристиками случайных величин используются и другие, более общие характеристики- начальные и центральные моменты, через которые, в частности, выражаются математическое ожидание и дисперсия.
Начальным моментом k-го порядка, или моментом k-го порядка, случайной величины X называется математическое ожидание k-й степени этой величины, т.е. vk=M( 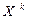 )
)
Если дискретная случайная величина X принимает значения х1,х2,..., хn,... с вероятностями р1,р2,..., рn,... то в соответствии с определением 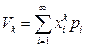 при условии, что этот ряд сходится абсолютно.
при условии, что этот ряд сходится абсолютно.
Центральным моментом k-го порядка случайной величины X называется математическое ожидание k-й степени отклонения этой величины от ее математического ожидания. Обозначив центральный момент k-го порядка через 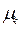 и положив М(Х)=a, по определению получим
и положив М(Х)=a, по определению получим
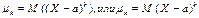 Если дискретная случайная величина принимает значение х1,х2,…,хn соответственно с вероятностями р1,р2,…рn…, то
Если дискретная случайная величина принимает значение х1,х2,…,хn соответственно с вероятностями р1,р2,…рn…, то 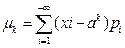 при условии, что ряд сходится абсолютно.
при условии, что ряд сходится абсолютно.
Эксцессом случайной величины Х называется число, определяется формулой 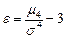 , где
, где 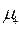 центральный момент четвертого порядка;
центральный момент четвертого порядка; 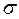 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Закон Пуассона.
Случайная величина Х распределена по закону Пуассона, если она принимает целые значения k = 0, 1, 2, ... с вероятностями 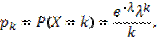 где
где 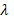 > 0 – параметр распределения. При этом
> 0 – параметр распределения. При этом 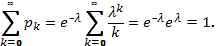
Значения вероятностей 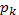 приводятся в таблицах распределения Пуассона.
приводятся в таблицах распределения Пуассона.
Математическое ожидание и дисперсия пуассоновской случайной величины равны параметру распределения: 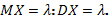
Распределение Пуассона используется для приближенных вычислений.
Геометрическое и гипергеометрическое распределения.
Дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения k=1, 2, 3, … с вероятностями 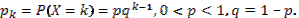
Определение является корректным, т.к. сумма вероятностей 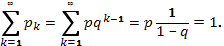
Случайная величина Х, имеющая геометрическое распределение, представляет собой число испытаний Бернулли до первого успеха.
Математическое ожидание и дисперсия Х: 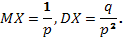
Дискретная случайная величина Х имеет гипергеометрическое распределение, если она принимает значения m с вероятностями 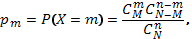 где m=0,1,…,k; k = min(n, M); M
где m=0,1,…,k; k = min(n, M); M 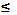 N; n
N; n 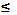 N.
N.
Вероятность 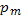 является вероятностью выбора m объектов обладающих заданным свойством, из множества n объектов, случайно извлечённых (без возврата) из совокупности N объектов, среди кот. Mобъектов обладают заданным свойством.
является вероятностью выбора m объектов обладающих заданным свойством, из множества n объектов, случайно извлечённых (без возврата) из совокупности N объектов, среди кот. Mобъектов обладают заданным свойством.
Математическое ожидание и дисперсия случайной величины, имеющей гипергеометрическое распределение с параметрамиn, M, N: 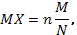
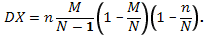
|
из
5.00
|
Обсуждение в статье: Моменты случайных величин |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

