 |
Главная |
Криволинейные интегралы второго рода
|
из
5.00
|
Определение
Предположим, что кривая C задана векторной функцией  , где переменная s − длина дуги кривой. Тогда производная векторной функции
, где переменная s − длина дуги кривой. Тогда производная векторной функции

представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1).
В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.


Рис.1 Рис.2
Введем векторную функцию  , определенную на кривой C, так, чтобы для скалярной функции
, определенную на кривой C, так, чтобы для скалярной функции 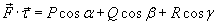
существовал криволинейный интеграл  . Такой интеграл
. Такой интеграл  называется криволинейным интегралом второго рода от векторной функции вдоль кривой C и обозначается как
называется криволинейным интегралом второго рода от векторной функции вдоль кривой C и обозначается как 
Таким образом, по определению,

где  − единичный вектор касательной к кривой C.
− единичный вектор касательной к кривой C.
Последнюю формулу можно переписать также в векторной форме: 
где  .
.
Если кривая C лежит в плоскости Oxy, то полагая R = 0, получаем 
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −C кривую противоположного направления - от B к A. Тогда

2. Если C − объединение кривых C1 и C2 (рисунок 2 выше), то

3. Если кривая C задана параметрически в виде  , то
, то

4. Если кривая C лежит в плоскости Oxy и задана уравнением  (предполагается, что R =0 и t = x), то последняя формула записывается в виде
(предполагается, что R =0 и t = x), то последняя формула записывается в виде
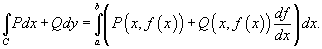
Пример 1
Вычислить интеграл  , где кривая C задана параметрически в виде
, где кривая C задана параметрически в виде  .
.
Решение. Используя формулу 
находим ответ: 
71.



72.Вычисление поверхностного интеграла.
Если существует конечный предел

не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек Mi  ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается
ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается

К использованию этих условий, равно как и условий, получающихся из них перестановкой переменных x, y, z сводится большинство практически встречающихся случаев по плоской области τ. Переходя к пределу, получаем:

73. формула Стокса, формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности S, ограниченной контуром L. Стокса формула имеет вид:
 ,
,
причём направление обхода контура L должно быть согласовано с ориентацией поверхности S. В векторной форме Стокса формула приобретает вид:
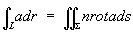 ,
,
где а = Pi + Qj + Rk, dr — элемент контура L, ds — элемент поверхности S, n — единичный вектор внешней нормали к этой поверхности.
74. Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля пообъёму, ограниченному этой поверхностью:
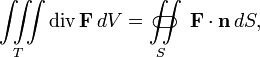
то есть интеграл от дивергенции векторного поля  , распространённый по некоторому объёму
, распространённый по некоторому объёму  , равен потоку вектора через поверхность
, равен потоку вектора через поверхность  , ограничивающую данный объём.
, ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.
В работе Остроградского формула записана в следующем виде:

где  и
и  — дифференциалы объёма и поверхности соответственно. В современной записи
— дифференциалы объёма и поверхности соответственно. В современной записи  — элемент объёма,
— элемент объёма,  — элемент поверхности.
— элемент поверхности.  — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
23.
| Метод замены переменной |
Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
 где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой. Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du. Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования.
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой. Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du. Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования.
|
|
из
5.00
|
Обсуждение в статье: Криволинейные интегралы второго рода |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

