 |
Главная |
Операции над множествами. Обозначение множеств и их элементов
|
из
5.00
|
Обозначение множеств и их элементов. Равенство множеств.
Подмножество ( включение ). Сумма ( объединение ) множеств.
Произведение ( пересечение ) множеств. Разность ( дополнение )
множеств.Симметричная разность множеств. Свойства
операций над множествами.
Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись a 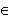 R означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут a
R означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут a  R .
R .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Говорят, что множество А содержится в множестве В ( рис.1 ) или множество А является подмножеством множества В ( в этом случае пишут А  В), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения:
В), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: 
 А и А
А и А  А .
А .

Сумма ( объединение ) множеств А и В ( пишется А  В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е
В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, е 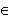 А
А  В тогда и только тогда, когда либо е
В тогда и только тогда, когда либо е 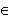 А ,либо е
А ,либо е 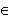 В .
В .
Произведение ( пересечение ) множеств А и В ( пишется А  В , рис.2 ) есть множествоэлементов, каждый из которых принадлежит и А , и В. Таким образом, е
В , рис.2 ) есть множествоэлементов, каждый из которых принадлежит и А , и В. Таким образом, е 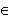 А
А  В тогда и только тогда, когда е
В тогда и только тогда, когда е 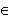 А и е
А и е 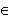 В .
В .

Разность множеств А и В ( пишется А – В , рис.3 ) есть множествоэлементов, которые принадлежат множеству А , но не принадлежат множеству В.Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется А \ В ) есть множество:
А \ В = ( А – В )  ( В – А ).
( В – А ).
Свойства операций над множествами:

П р и м е р ы. 1. Множество детей является подмножеством всего населения.
2. Пересечением множества целых чисел с множеством поло-
жительных чисел является множество натуральных чисел.
3. Объединением множества рациональных чисел с множест-
вом иррациональных чисел является множество действи-
тельных чисел.
4. Нуль является дополнением множества натуральных чисел
относительно множества неотрицательных целых чисел.
Множество  содержится во множестве
содержится во множестве  (множество
(множество  включает множество
включает множество  ), если каждый элемент
), если каждый элемент  есть элемент
есть элемент  :
:

В этом случае  называется подмножеством
называется подмножеством  ,
,  — надмножеством
— надмножеством  . Если
. Если  и
и  , то
, то  называется собственным подмножеством
называется собственным подмножеством  . Заметим, что
. Заметим, что  . По определению
. По определению  .
.
Два множества называются равными, если они являются подмножествами друг друга:

Иногда для того, чтобы подчеркнуть, что множества могут быть равны, используется запись:

Бинарные операции
Ниже перечислены основные операции над множествами:
· пересечение:

· объединение:

Если множества  и
и  не пересекаются:
не пересекаются:  , то их объединение обозначают также:
, то их объединение обозначают также:  .
.
· разность (дополнение):

· симметрическая разность:

· Декартово или прямое произведение:

Для лучшего понимания смысла этих операций используются диаграммы Эйлера — Венна, на которых представлены результаты операций над геометрическими фигурами как множествами точек.
Билет 2.
Правило вида f: A->B, ставящее в соответствие каждому элементу множества A какой-либо элемент (или элементы) множества B, называется отображением из A в B. Пример: A - множество футбольных команд, B - множество населённых пунктов; каждой футбольной команде ставится в соответствие пункт, где находится её родной стадион (ну или стадион, где она официально играет "на своём поле", если нет собственного стадиона).
Если какому-либо элементу множества A соответствует более одного элемента множества B, то отображение многозначное. Пример многозначного изображения можно привести следующий. Пусть A - множество олигархов, B - множество особняков. Есть олигархи, владеющие несколькими особняками. Тогда отображение, ставящее в соответствие каждому олигарху его особняки, является многозначным.
В дискретной математике, как правило, рассматриваются однозначные отображения. Отображение из A в B однозначное, если всякому элементу из A поставлен в соответствие только один элемент из B. Пример однозначного отображения: пусть есть воинская часть, в ней множество солдат и множество батальонов. Отображение, ставящее в соответствие солдату батальон, в котором он числится, однозначное, если только в списках составов не допущено ошибок. Заметим, что определение однозначного отображения из A в B не запрещает ситуаций, когда двум разным элементам множества A соответствует один и тот же элемент из B. Ярко видно это по примеру с солдатами.
Далее мы рассмотрим некоторые виды однозначных отображений, для простоты понятие "однозначное" иногда будем опускать.
|
из
5.00
|
Обсуждение в статье: Операции над множествами. Обозначение множеств и их элементов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

