 |
Главная |
Дифференцирование функций
|
из
5.00
|
Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда при-ращение аргумента стремится к нулю:
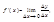
где 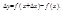
Производная обозначается у', y'(x), y'x.
Правила дифференцирования функций. Пусть С – постоянная, а u(x) и v(x) – дифференцируемые функции. Тогда C' = 0,

Производная сложной функции y = f(u(x)). Если функция u = u(x) дифференцируема в точке х, а функция y = f(u) дифференцируемая в соответствующей точке u = u(x), то сложная функция y = f(u(x)) дифференцируема в точке х и ее производная равна
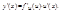
Таблица производных
1. 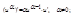
2.  3.
3. 
4.  5.
5. 
6. 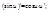 7.
7. 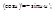
8. (  9.
9. 
10. 
11. 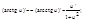
12. 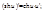 13.
13. 
14. 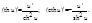
Функция  неявно задана уравнением
неявно задана уравнением 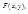 если для всех
если для всех  выполняется равенство
выполняется равенство 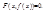
Для вычисления производной функции, заданной неявно, следует тождество 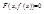 продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x)
продифференцировать по х (рассматривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x)
Производные и дифференциалы высших порядков.
Дифференцирование функций, заданных параметрически
Производной второго порядка функции 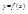 называется производная от ее производной
называется производная от ее производной 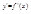 , т.е.
, т.е.  . Аналогично определяются производные более высоких порядков
. Аналогично определяются производные более высоких порядков 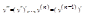 .
.
Дифференциалы высших порядков функции 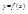 (x – независимая переменная) вычисляются по формулам
(x – независимая переменная) вычисляются по формулам
 .
.
Если функция 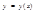 задана параметрически соотношениями
задана параметрически соотношениями 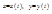 , причем
, причем  , то ее первая
, то ее первая 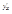 и вторая
и вторая 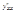 производные находятся по формулам:
производные находятся по формулам:
 .6.3.
.6.3.
Теорема Ролля. Если функция 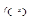 непрерывна на отрезке
непрерывна на отрезке 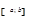 , дифференцируема на интервале
, дифференцируема на интервале 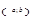 и
и 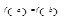 , то существует хотя бы одна точка
, то существует хотя бы одна точка 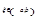 такая, что
такая, что 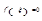 .
.
Теорема Лагранжа. Если функция 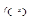 непрерывна на отрезке
непрерывна на отрезке 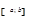 и дифференцируема на интервале
и дифференцируема на интервале 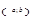 , то существует точка
, то существует точка 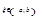 такая, что
такая, что 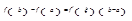 (формула Лагранжа).
(формула Лагранжа).
Теорема Коши. Если функции 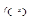 и
и  непрерывны на отрезке
непрерывны на отрезке 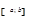 , дифференцируемы на интервале
, дифференцируемы на интервале 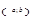 и
и 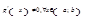 , то существует точка
, то существует точка 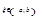 такая, что
такая, что 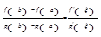 (формула Коши).
(формула Коши).
Правило Лопиталя (раскрытие неопределенностей 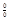 и
и 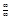 ).
).
Пусть 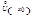 – окрестность точки
– окрестность точки  с выброшенной точки
с выброшенной точки  .
.
Теорема. Пусть функции 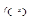 и
и  дифференцируемы на
дифференцируемы на 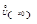 ;
; 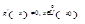 .
.
Если 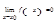 и
и  (или
(или 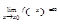 и
и 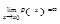 ), то
), то 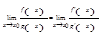 при условии, что сущест-вует предел отношения производных.
при условии, что сущест-вует предел отношения производных.
Замечания:1. Аналогичная теорема справедлива и в случае 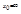 .
.
2. Если частное 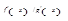 в точке
в точке  также есть неопределенность вида
также есть неопределенность вида 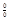 или
или 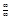 и производные
и производные 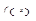 и
и 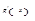 удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д.
удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д.
3. Неопределенности вида  или
или 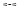 алгебраическими пре-образованиями функции приводятся к неопределенности вида
алгебраическими пре-образованиями функции приводятся к неопределенности вида 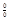 или
или  , и далее применяется правило Лопиталя.
, и далее применяется правило Лопиталя.
4. В случае неопределенности вида  , или
, или 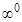 , или
, или  следует прологарифмировать функцию и предварительно найти предел ее логарифма.
следует прологарифмировать функцию и предварительно найти предел ее логарифма.
|
из
5.00
|
Обсуждение в статье: Дифференцирование функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

