 |
Главная |
Формулы включения-исключения
|
из
5.00
|
Комбинаторика. Правила суммы и произведения, формула включения и исключения, примеры применения. Сочетатания, перестановки, размещения, числа Стирлинга первого и второго рода, комбинаторный смысл этих чисел.
Совокупность 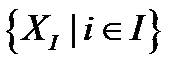 подмножеств множества X называется покрытием множества X если
подмножеств множества X называется покрытием множества X если  ,
,  -блок покрытия.
-блок покрытия.
Совокупность подмножеств множества X называется разбиением множества X, если
1.  2.
2.  3.
3. 
Правило суммы.Если  разбиение множества X, то
разбиение множества X, то 
Док-во.(по индукции)
База: m=2. 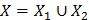 =>
=> 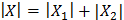
Шаг индукции: k→k+1
X= 
|Х|=  =
= 
Ч. Т. Д.
Пример 1.X- n-множество, Y- k-множество,  . Обозначим
. Обозначим  число k-подмножеств Y в множестве X.
число k-подмножеств Y в множестве X.
1.  2.
2.  3.
3. 
C – семейство k-подмножеств, множества X. 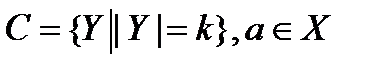
Разделим C на два класса. В класс С1 запишем те k-подмножества Y, которые содержат элемент a  . В класс С2 запишем все k-множества Y, которые не содержат а:
. В класс С2 запишем все k-множества Y, которые не содержат а: 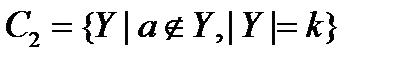 .
.

Пример 2:
 число способов выбора k элементов из X, среди которых нет двух соседних
число способов выбора k элементов из X, среди которых нет двух соседних
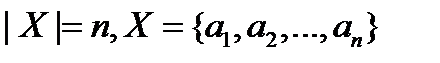 ,
, 
Все выборки разделим на два класса:
1. Содержит 
2. Не содержит 
тогда 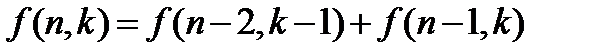
Правило произведения
Для любых конечных множеств  справедливо равенство
справедливо равенство 
Доказательство по индукции:
Шаг индукции k=2

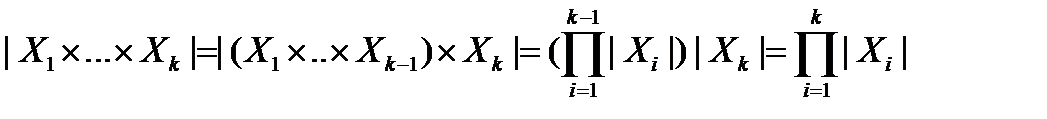
Формулы включения-исключения
Характеристическая функция подмножества Y из множества X определяется:
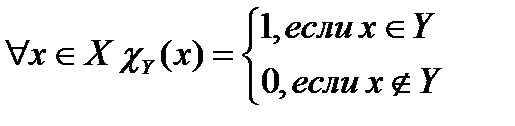
Теорема: Пусть  -совокупность подмножеств множества X,
-совокупность подмножеств множества X,  . Тогда
. Тогда 
J пробегает все непустые подмножества множества I
Доказательство: Будем опираться на 2 тождества
1. 

2. Понятие характеристической функции

Доказательство: посчитаем вклад  в правую и левую часть доказанной формулы.
в правую и левую часть доказанной формулы.
Обозначим  , тогда
, тогда 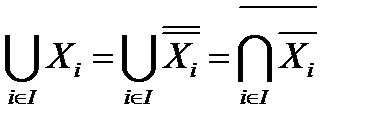

Просуммируем формулу по  , т.к. формула только для фиксированного x.
, т.к. формула только для фиксированного x.


Учитывая, что по свойству характеристической функции 
получаем  . Заметим, что формула принимает более простой вид, когда
. Заметим, что формула принимает более простой вид, когда
I={1,2,…,n} : 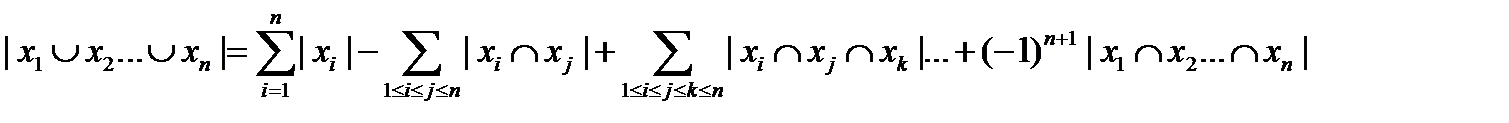
В частности для n=2
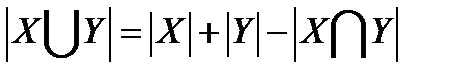
Пример: Задача о беспорядках.Подстановка  называется беспорядком, если у нее нет неподвижных точек, т.е.
называется беспорядком, если у нее нет неподвижных точек, т.е.  . Рассмотрим
. Рассмотрим  -группу подстановок,
-группу подстановок,  . Посчитаем количество беспорядков в ней. Обозначим
. Посчитаем количество беспорядков в ней. Обозначим  -число беспорядков в
-число беспорядков в  .
.  .
. 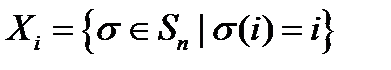
 Заметим, что
Заметим, что  .
. 
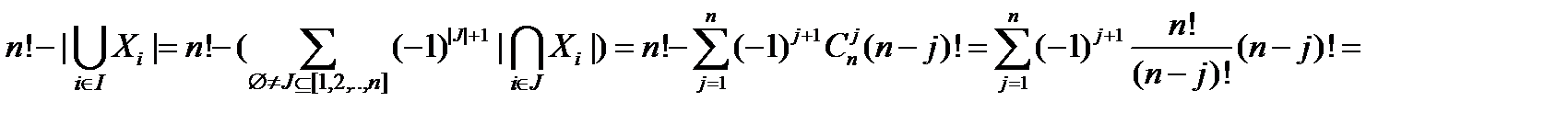

Перестановка без повторений – это размещение из m элементов по m без повторений.

Перестановка с повторением.Пусть имеются k предметы различных типов. Предметов первого типа -  штук, второго -
штук, второго - 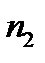 и т. д.
и т. д. 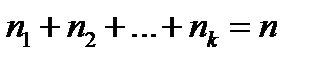 . Если бы все предметы были различны, то число перестановок было бы n!. Рассмотрим перестановку вида
. Если бы все предметы были различны, то число перестановок было бы n!. Рассмотрим перестановку вида  (*). Элементы первого типа можно переставлять друг с другом
(*). Элементы первого типа можно переставлять друг с другом  способами, при этом общая перестановка не меняется. Аналогично для
способами, при этом общая перестановка не меняется. Аналогично для 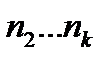 . Получим, что элементы перестановки (*) можно переставлять друг с другом
. Получим, что элементы перестановки (*) можно переставлять друг с другом  способами (т.к. перестановки элементов первого типа, второго и т.д. можно делать независимо друг от друга). Значит, число различных перестановок с повторениями будет
способами (т.к. перестановки элементов первого типа, второго и т.д. можно делать независимо друг от друга). Значит, число различных перестановок с повторениями будет 
Сочетанием без повторений из n по k называется набор k элементов, выбранных из данных n элементов. Составим сначала все k сочетания из n элементов. Переставим входящие в каждое сочетание элементы всеми возможными способами, и получим, что из каждого k-сочетания можно получить k! штук k-размещений.

Сочетания с повторениями.Пара  состоящая из множества X, где
состоящая из множества X, где  и неотрицательной функции
и неотрицательной функции 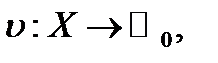 где
где  , называется k-мультимножеством, если
, называется k-мультимножеством, если 
 .
.  называется кратностью вхождения элемента x в k-мультимножество
называется кратностью вхождения элемента x в k-мультимножество  . Носителем мультимножества
. Носителем мультимножества  называется множество элементов
называется множество элементов 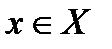 , для которых
, для которых 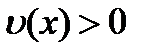 .
.
 -количество k-мультимножеств на n-множестве.
-количество k-мультимножеств на n-множестве.
Пусть 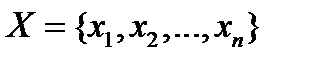 . Надо посчитать количество решений уравнения
. Надо посчитать количество решений уравнения  .
.
Каждому решению поставим в соответствие элемент из 
 . Всего k едениц и n-1 нулей. Задача свелась к нахождению количества способов расстановки n-1 нулей k+n-1 мест
. Всего k едениц и n-1 нулей. Задача свелась к нахождению количества способов расстановки n-1 нулей k+n-1 мест 
Числа Стирлинга 2-го рода.Пусть |Y|=m. Разбиваем на k блоков. Рассмотрим неупорядоченное разбиение. Обозначим через S(m,k) число неупорядоченных разбиений множества Y на k блоков.
S(m, k ) – числа Стирлинга 2-го рода. Пусть S(0,0) = 1
Возьмем k>m.
 ,
, 

Возьмем 2 < k < m и выведем рекуррентную формулу. Возьмем 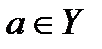 - фиксируем.
- фиксируем.  полученное множество надо разбить на k блоков. S(m-1, k ) и помещаем элемент а в любой из этих блоков
полученное множество надо разбить на k блоков. S(m-1, k ) и помещаем элемент а в любой из этих блоков  . Если элемент a образует блок , состоящий из одного элемента, тогда для остальных k-1 блоков
. Если элемент a образует блок , состоящий из одного элемента, тогда для остальных k-1 блоков 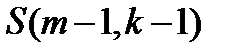 .
. 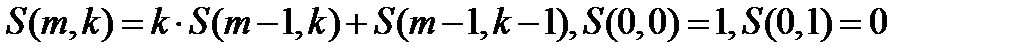
|
из
5.00
|
Обсуждение в статье: Формулы включения-исключения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

