 |
Главная |
Конечные автоматы и формальные языки
|
из
5.00
|
Определение детерминированного конечного автомата, способы его задания. Расширенные функции переходов на цепочки. Язык ДКА.
Алфавитом называется конечное непустое множество символов. Пример: бинарный алфавит  = {0, 1}. Цепочкой или словом называется любая последовательность символов из некоторого алфавита.
= {0, 1}. Цепочкой или словом называется любая последовательность символов из некоторого алфавита.  - пустая цепочка (пустое слово) не содержит ни одного символа.
- пустая цепочка (пустое слово) не содержит ни одного символа. 
Длина слова – число позиций для символов в цепочке. Пример: 01100. Символов – 2 длина – 5. 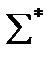 - все слова в алфавите
- все слова в алфавите 
Множество слов каждое из которых принадлежит 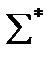 называется языком L.
называется языком L.
Детерминированным конечным автоматом (ДКА) называется пятерка A = (Q,  ,
,  ,
, 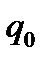 , F)
, F)
Q – непустое конечное множество (множество состояний).  - алфавит, множество входных символов.
- алфавит, множество входных символов. 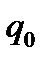 - начальное состояние.
- начальное состояние. 
F – множество допустимых (заключительных) состояний
 ,
, 
Язык ДКА – множество всех его допустимых цепочек. Любой ДКА определяет язык, а именно множество всех цепочек приводящих автомат из начального состояния в одно из допускающих. Язык ДКА – множество всех меток вдоль всех маршрутов, ведущих из начального состояния в любое допускающее.
 ,
, 
 - расширенная функция переходов,
- расширенная функция переходов, 
Индукция по длине слова
| w | - количество позиций в слове
| w | = 0 
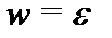 ,
,  ,
,  ,
, 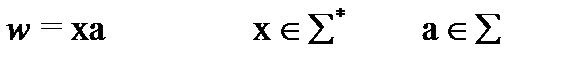
x – начальное слово, a – алфавитный символ, 
 Язык ДКА A = (Q,
Язык ДКА A = (Q,  ,
,  ,
, 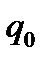 , F),
, F), 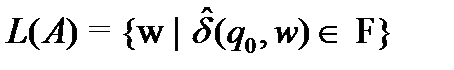 такие слова, которые приводят начальное состояние в конечное. Язык L называется регулярным, если L = L(A) (если совпадает с языком некоторого автомата).
такие слова, которые приводят начальное состояние в конечное. Язык L называется регулярным, если L = L(A) (если совпадает с языком некоторого автомата).
Определение недетерминированного конечного автомата, способы его задания. Расширенные функции переходов на цепочки. Язык НКА.
НКА обладает свойством находиться в нескольких состояниях одновременно. Эту особенность часто представляют как свойство автомата “делать догадки” относительно его входных данных. Нужно: 1. определить НКА 2. показать, что всякий такой автомат допускает язык допустимый ДКА.
НКА допускает регулярные языки точно так же как и ДКА.
НКА автоматы строить легче, можно преобразовать в ДКА.
A = (Q,  ,
,  ,
, 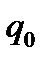 , F),
, F), 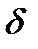 - функция перехода
- функция перехода
Различие ДКА и НКА состоит в типе функции  .
.
НКА 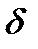 функция, аргументами которой являются состояния и элемент входного алфавита, а значениями
функция, аргументами которой являются состояния и элемент входного алфавита, а значениями 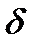 - множество состоящее из 0,1 или нескольких состояний.
- множество состоящее из 0,1 или нескольких состояний.
Язык НКА.НКА допускает цепочку w, если в процессе чтения этой цепочки можно выбрать хотя бы 1 последовательность переходов, так чтобы перейти из начального состояния в одно из допускающих. Тот факт, что при другом последовательности переходов по символам цепочки  мы можем попасть в недопускающее состояние или вообще не попасть ни в какое, совсем не означает
мы можем попасть в недопускающее состояние или вообще не попасть ни в какое, совсем не означает  не является допустимым.
не является допустимым.
Для данного НКА A = (Q,  ,
,  ,
, 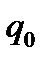 , F) язык L(A) есть множество цепочек
, F) язык L(A) есть множество цепочек 
|
из
5.00
|
Обсуждение в статье: Конечные автоматы и формальные языки |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

