 |
Главная |
Признак возрастания и убывания функции
|
из
5.00
|
Линии второго порядка на плоскости.
Линии, уравнения которых в прямоугольной систем координат являются уравнениями второй степени, называются линиями второго порядка.К важнейшим линиям второго порядка относятся эллипс, окружность, гипербола и парабола.
Эллипс. Окружность.
Определение 4.1. Эллипсомназывается множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.
 Пусть F1(-c,0) и F2(c,0) ─ фокусы. Тогда F1F2 = 2c ─ фокусное расстояние(рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.
Пусть F1(-c,0) и F2(c,0) ─ фокусы. Тогда F1F2 = 2c ─ фокусное расстояние(рис.4.1). Постоянную величину, о которой идёт речь в определении эллипса, обозначим 2a.
Пусть M(x,y) ─ произвольная точка эллипса. Тогда по определению F1M + F2M = 2a > 2c, откуда a > c.
Так как F1M = 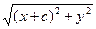 , F2M =
, F2M = 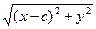 , то имеем уравнение
, то имеем уравнение 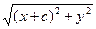 +
+ 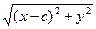 = 2a.
= 2a.
Преобразуем это уравнение:
( 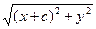 )2 = (2a −
)2 = (2a − 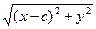 )2 ,
)2 ,
(x2 + 2cx + c2) + y2 = 4a2 – 4a 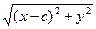 + (x2 – 2cx + c2) + y2,
+ (x2 – 2cx + c2) + y2,
a 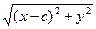 = a2 – cx.
= a2 – cx.
Возводя в квадрат последнее уравнение, имеем
a2(x2 – 2cx + c2 + y2) = a4 – 2cxa2 + c2x2,
(a2 – c2)x2 + a2y2 = a2(a2 – c2).
Так как a > c, то a2 – c2 > 0 и можем обозначить b2 = a2 – c2. Тогда
b2x2 + a2y2 = a2b2,
 = 1 (1)
= 1 (1)
Таким образом, координаты любой точки эллипса удовлетворяют уравнению (1).
Покажем обратное: если координаты точки M(x,y) удовлетворяют уравнению (1), то точка M лежит на эллипсе.
Из (1) найдём y2 : y2 = b2(1 -  ).
).
Тогда F1M = 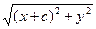 =
=  = =
= =  =
= 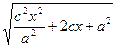 =
=  = │
= │  │
│
Т.к. c < a и из (1)  ≤ 1, т.е. x2 ≤ a2 , │x│ ≤ a, то
≤ 1, т.е. x2 ≤ a2 , │x│ ≤ a, то  . Следовательно,
. Следовательно,
│  │=
│=  .
.
Аналогично можно вычислить
F2M =  .
.
Теперь
F1M + F2M =  .
.
Из уравнения (1) : b2 > 0 Þ a2 – c2 > 0, т.е. a > c, откуда 2a > 2c. Значит, точка M лежит на эллипсе.
Уравнение (1) называется каноническим уравнением эллипса.Изображён эллипс с уравнением (1) на рис 4.2.
 Точки пересечения эллипса с осями координат называются вершинами эллипса.Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осяминазывают также отрезки A1A, B1B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью,b ─ малой полуосью. Эксцентриситетом эллипсаназывается отношение фокусного расстояния к длине большой оси, т.е.
Точки пересечения эллипса с осями координат называются вершинами эллипса.Оси симметрии эллипса (оси Ox и Oy) называют осями эллипса. Точка пересечения осей ─ центр эллипса. Осяминазывают также отрезки A1A, B1B. Отрезки OA, OB и их длины называют полуосями. В нашем случае a > b, поэтому а называют большой полуосью,b ─ малой полуосью. Эксцентриситетом эллипсаназывается отношение фокусного расстояния к длине большой оси, т.е.
ε = 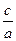 .
.
Так как 0  c < a, то 0
c < a, то 0  ε < 1. Фокальными радиусами точки Mназывают отрезки F1M и F2M. Их длины r1 и r2 вычисляют по формулам
ε < 1. Фокальными радиусами точки Mназывают отрезки F1M и F2M. Их длины r1 и r2 вычисляют по формулам
r1 = a + εx,
r2 = a – εx.
 Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a2 = b2 – c2.
Уравнение (1) можно рассматривать и в случае, когда b > a, оно определяет эллипс с большой полуосью OB = b, фокусы такого эллипса лежат на оси Oy, причём a2 = b2 – c2.
В случае, когда a = b, уравнение (1) принимает вид
 = 1 или x2 + y2 = a2
= 1 или x2 + y2 = a2
и определяет окружность радиуса а с центром в начале координат (рис.4.3). В этом случае c = 0, поэтому ε = 0.
Из школьного курса известно уравнение окружности радиуса R с центром в точке A0(x0,y0):
(x – x  )
)  +(y – y
+(y – y  )
)  =R
=R  .
.
Такое уравнение называют каноническим уравнением окружности.
Гипербола.
Определение 4.2. Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек, называемыхфокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Пусть F1(-c,0) и F2(c,0) ─ фокусы. Тогда F1F2 = 2c ─ фокусное расстояние (рис.4.4). Постоянную величину, о которой идёт речь в определении, обозначим 2a. Тогда по определению 2a < 2c, т.е. a < c.
Пусть M(x;y) ─ произвольная точка гиперболы. Рассуждая по аналогии с п. 4.1, можем получить уравнение
 = 1, (2)
= 1, (2)
где b2 = c2 – a2.
Уравнение (2) называют каноническим уравнением гиперболы. Гипербола с уравнением (2) изображена на рис.4.5.
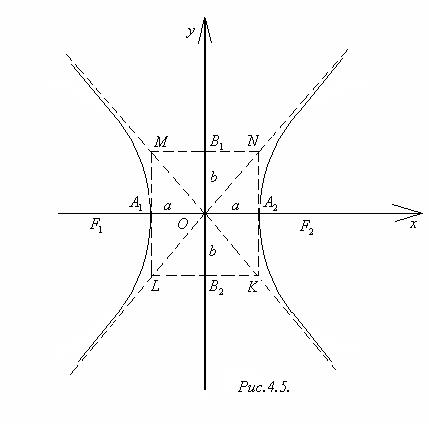
Прямоугольник MNKL, стороны которого MN = LK = 2a, ML = NK = 2b, называется основным прямоугольником. Прямые MK и NL называют асимптотами гиперболы,их уравнения : y = – 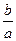 x и y =
x и y = 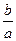 x, соответственно. Гипербола имеет две ветви: левую и правую. Центр симметрии гиперболы называется её центром. Оси симметрии гиперболы называются её осями. Одна ось пересекает гиперболу в двух точках (на рис.4.5 это т. A1 и A2), эта ось называется действительной осью гиперболы,другая ось ─ мнимой осью, она не имеет общих точек с гиперболой. Длины отрезков A1A2 и B1B2 также называют осями. Величины a и b называются полуосями гиперболы. Если a = b, то гипербола называется равносторонней,её уравнение
x, соответственно. Гипербола имеет две ветви: левую и правую. Центр симметрии гиперболы называется её центром. Оси симметрии гиперболы называются её осями. Одна ось пересекает гиперболу в двух точках (на рис.4.5 это т. A1 и A2), эта ось называется действительной осью гиперболы,другая ось ─ мнимой осью, она не имеет общих точек с гиперболой. Длины отрезков A1A2 и B1B2 также называют осями. Величины a и b называются полуосями гиперболы. Если a = b, то гипербола называется равносторонней,её уравнение
x2 – y2 = a2.
Уравнение
-  = 1 (3)
= 1 (3)
определяет гиперболу с действительной осью Oy (рис.4.6).
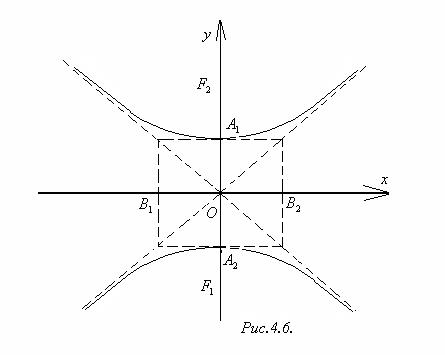
Гиперболы, определяемые уравнениями (2) и (3) в одной и той же системе координат, называются сопряжёнными. Эксцентриситет гиперболы─ это отношение фокусного расстояния к расстоянию между вершинамигиперболы (т.е. точками пересечения гиперболы с осями). Для уравнения (2)
ε = 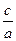 .
.
Так как c > a, то ε > 1. Фокальные радиусы точки M гиперболы─ это отрезки F1M и F2M. Их длины r1 и r2 для правой ветви
r1 = εx + a, r2 = εx – a,
для левой ветви
r1 = -εx − a, r2 = - εx + a.
Парабола.
 Определение 4.3. Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и данной прямой, называемой директрисой, и не проходящей через фокус.
Определение 4.3. Параболойназывается множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и данной прямой, называемой директрисой, и не проходящей через фокус.
Возьмём в прямоугольной системе координат точку F(  ,0), где p > 0 и пусть она будет фокусом. Директрисой будет прямая x = -
,0), где p > 0 и пусть она будет фокусом. Директрисой будет прямая x = -  (рис.4.7). Пусть M(x,y) ─ произвольная точка параболы. Если K ─ основание перпендикуляра из точки M к директрисе, то она имеет координаты (-
(рис.4.7). Пусть M(x,y) ─ произвольная точка параболы. Если K ─ основание перпендикуляра из точки M к директрисе, то она имеет координаты (-  ,y). По определению 4.3
,y). По определению 4.3
MK = MF.
Тогда
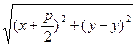 =
=  ,
, 
 =
=  , т.к. x ≥ 0.
, т.к. x ≥ 0.
Возводим уравнение а квадрат и приводим подобные члены:
 ,
,
y2 = 2px (4)
 Уравнение (4) называется каноническим уравнением параболы. Величину p называют параметром параболы. Парабола с уравнением (4) изображена на рис.4.8. Точка O называется вершиной параболы,ось симметрии ─ осью параболы. Если парабола имеет уравнение y2 = - 2px, то её график расположен слева от оси Oy (рис.4.9). Уравнения x2 = 2pyи x2 = -2py, p > 0 определяют параболы, изображённые на рис.4.10 и рис.4.11, соответственно.
Уравнение (4) называется каноническим уравнением параболы. Величину p называют параметром параболы. Парабола с уравнением (4) изображена на рис.4.8. Точка O называется вершиной параболы,ось симметрии ─ осью параболы. Если парабола имеет уравнение y2 = - 2px, то её график расположен слева от оси Oy (рис.4.9). Уравнения x2 = 2pyи x2 = -2py, p > 0 определяют параболы, изображённые на рис.4.10 и рис.4.11, соответственно.
Исследование функций
Признак возрастания и убывания функции. Экстремум функции. Необходимое и достаточное условие экстремума. Направления выпуклости, точки перегиба. Асимптоты. Исследование функций и построение графиков.
Признак возрастания и убывания функции.
Определение.Функция у = f(x) на интервале (  ) называется:
) называется:
а) постоянной, если f(x) = c, где с = const, для любого хÎ(  );
);
б) возрастающей,если для любых двух значений х1, х2Î(  ) из неравенства х1 < х2
) из неравенства х1 < х2
следует неравенство f(x1) < f(x2);
в) убывающей,если для любых двух значений х1, х2Î(  ) из неравенства х1 < х2 следует
) из неравенства х1 < х2 следует
неравенство f(x1) > f(x2).
|
из
5.00
|
Обсуждение в статье: Признак возрастания и убывания функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

