 |
Главная |
Тема 4.1.Первообразная. Неопределенный интеграл
|
из
5.00
|
Функция F(x) называется первообразной для функции f(x) на промежутке (a;b), если для всех xÎ(a;b) выполняется равенство F¢(x) = f(x).
Например, для функции x2 первообразной будет функция x3/3.
Если для F(x) установлено равенство dF(x) = f(x)dx, то F(x) ¾ первообразная для f(x), так как 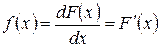 .
.
Рассмотрим две теоремы, которые называются теоремами об общем виде всех первообразных данной функции.
Теорема 1. Если F(x) – первообразная для f(x) на (a;b), то F(x) + C, где C – число, тоже первообразная для f(x) на (a;b).
Доказательство.
(F + C)¢ = F¢ + C¢ = f + 0 = f
По определению F + C ¾ первообразная для f.
Прежде чем рассмотреть теорему 2, докажем две вспомогательные теоремы.
Если функция g(x) постоянна на (a;b), то g¢(x) = 0.
Доказательство.
Так как g(x) = C, справедливы равенства: g¢(x) = C¢ = 0 (здесь, как и ниже, через C обозначено произвольно выбранное число).
Если g¢(x) = 0 при всех xÎ(a;b), то g(x) = C на (a;b).
Доказательство.
Пусть g¢(x) = 0 во всех точках (a;b). Зафиксируем точку x1Î(a;b). Тогда для любой точки xÎ(a;b) по формуле Лагранжа имеем
g(x) – g(x1) = g¢(x)(x – x1)
Так как xÎ(x; x1), а точки x и x1 принадлежат промежутку (a;b), то g¢(x) = 0, откуда следует, что g(x) – g(x1)=0, то есть g(x) = g(x1)=const.
Теорема 2. Если F(x) есть первообразная для f(x) на промежутке (a;b), а G(x) – другая первообразная для f(x) на (a;b), то G = F + C, где C – число.
Доказательство.
Возьмем производную от разности G – F: (G – F)¢ = G¢ – F¢ =
= f – f = 0. Отсюда следует: G – F = C, где C ¾ число, то есть G = F + C.
Множество всех первообразных для функции f(x) на промежутке (a;b)называется неопределенным интегралом и обозначается òf(x)dx. Если F(x) – первообразная для f(x), то òf(x)dx = F(x) + C, где C – произвольное число (constanta).
Вычисление неопределенного интеграла от заданной функции называется интегрированием.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления F¢(x) = f(x) соответствует формула òf(x) dx = F(x) + C интегрального исчисления. Отсюда получается таблица неопределенных интегралов.
Но прежде отметим, как и в дифференциальном исчислении, буква u может обозначать как независимую переменную x (u=x), так и функцию от независимой переменной (u=u(x)).
1. 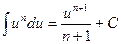 (n≠-1).
(n≠-1).
2. 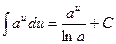 (a >0, a≠1).
(a >0, a≠1).
3. 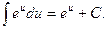
4. 
5. 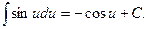
6. 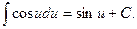
7. 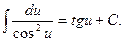
8. 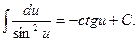
9. 
10. 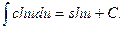
11. 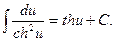
12. 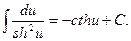
13. 13. 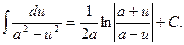
14.  (a≠0).
(a≠0).
15. 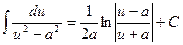 (a≠0).
(a≠0).
16. 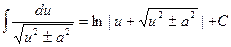 (|u| > |a|).
(|u| > |a|).
17. 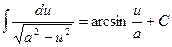 (|u|<|a|).
(|u|<|a|).
Интегралы 1 – 17 называют табличными. Некоторые из приведенных выше формул таблицы интегралов, не имеющие аналога в таблице производных, проверяются дифференцированием их правых частей.
Неопределенный интеграл обладает следующими свойствами:
1. Производная из неопределенного интеграла равна подынтегральной функции, дифференциал неопределенного интеграла равен подынтегральному выражению:
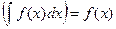 и
и 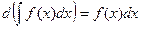 .
.
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
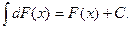
3. Постоянный множитель а (а≠0) можно выносить за знак неопределенного интеграла:


4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:
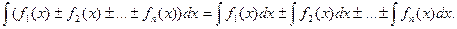
5. Если F(x) – первообразная функции f(x), то:
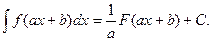
6 (инвариантность формул интегрирования). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной:
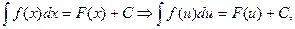
где u – дифференцируемая функция.
Все эти свойства непосредственно следуют из определения.
|
из
5.00
|
Обсуждение в статье: Тема 4.1.Первообразная. Неопределенный интеграл |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

