 |
Главная |
ДЕ4. Дифференциальное и интегральное исчисление
|
из
5.00
|
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дифференциал функции  равен
равен 
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке

Равна 
Решение:
Площадь данной фигуры можно вычислить по формуле  , где а-«левая» точка пересечения параболы и оси Ох,
, где а-«левая» точка пересечения параболы и оси Ох,  , а
, а 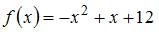 . Определим точки пересечения параболы и оси
. Определим точки пересечения параболы и оси  , решив уравнение
, решив уравнение  .Получаем:
.Получаем: 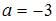 .
.

Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции  равно 2.
равно 2.
Решение:
Точку  называют точкой разрыва функции
называют точкой разрыва функции  , если она не является непрерывной в этой точке. В частности, точками разрыва данной функции могут являться точки, в которых знаменатель равен нулю, то есть
, если она не является непрерывной в этой точке. В частности, точками разрыва данной функции могут являться точки, в которых знаменатель равен нулю, то есть 


 . Однако область определения функции
. Однако область определения функции  определяется как
определяется как  , то есть имеет вид
, то есть имеет вид  . Тогда
. Тогда 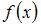 имеет 2 точки разрыва.
имеет 2 точки разрыва. 
 , удовлетворяющие условию
, удовлетворяющие условию  .
.
Тема: Дифференциальное исчисление ФНП
Частная производная 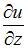 функции
функции 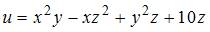 имеет вид
имеет вид 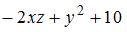 .
.
Тема: Непрерывность функции, точки разрыва
Точка  является точкой разрыва функции …
является точкой разрыва функции … 
Решение:
Точку  называют точкой разрыва функции
называют точкой разрыва функции  , если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть
, если она не является непрерывной в этой точке. В частности, точками разрыва данных функций являются точки, в которых знаменатель равен нулю, то есть  , или:
, или: 
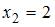 . Точка
. Точка 
не является точкой разрыва функции  , так как область определения функции
, так как область определения функции  имеет вид
имеет вид  ,и
,и  ;
;
не является точкой разрыва функции  , так как область определения функции
, так как область определения функции 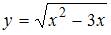 имеет вид
имеет вид  , и
, и 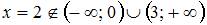 ;
;
не является точкой разрыва функции 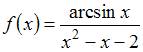 , так как область определения функции
, так как область определения функции  имеет вид
имеет вид  , и
, и  .
.
Таким образом, точка  является точкой разрыва функции
является точкой разрыва функции  .
.
Тема: Дифференциальное исчисление ФНП
Смешанная частная производная второго порядка 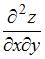 функции
функции 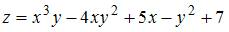 имеет вид …
имеет вид … 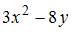
Тема: Приложения определенного интеграла
Площадь фигуры, ограниченной параболой 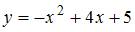 и осью
и осью  , равна …
, равна …

|
Решение:
Площадь данной фигуры можно вычислить по формуле  где
где 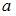 и
и 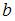 – это точки пересечения параболы и оси
– это точки пересечения параболы и оси  , а
, а 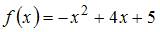 . Определим точки пересечения параболы и оси
. Определим точки пересечения параболы и оси 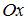 , решив уравнение
, решив уравнение 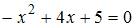 . Получаем:
. Получаем: 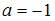 и
и 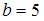 . Тогда
. Тогда 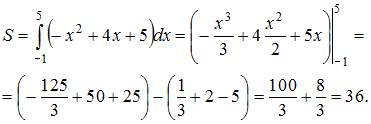
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дифференциал второго порядка функции  равен …
равен …

| 
|
Решение:
Дифференциал второго порядка 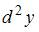 функции
функции  выражается формулой
выражается формулой 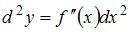 .Тогда вычислив
.Тогда вычислив  и
и  получаем
получаем  .
.
Тема: Дифференциальное исчисление ФНП
Частная производная 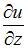 функции
функции 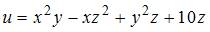 имеет вид …
имеет вид …

| 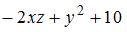
| ||
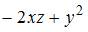
| |||
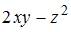
| |||
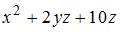
|
Решение:
При вычислении частной производной 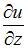 по переменной
по переменной  , переменные
, переменные 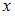 и
и 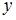 рассматриваем как постоянные величины. Тогда
рассматриваем как постоянные величины. Тогда
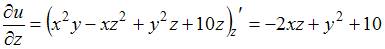 .
.
Тема: Непрерывность функции, точки разрыва
Для функции  точка
точка 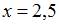 является точкой …
является точкой …

| разрыва второго рода | ||
| разрыва первого рода | |||
| непрерывности | |||
| устранимого разрыва |
Решение:
Вычислим односторонние пределы функции 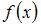 в точке
в точке 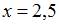 :
:
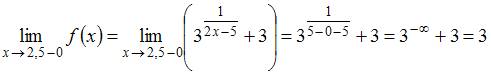 ,
,
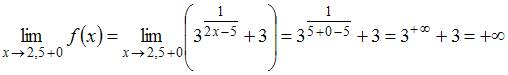 .
.
Так как один из односторонних пределов в точке 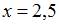 , а именно
, а именно 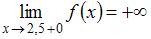 , то точка
, то точка 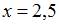 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дифференциал функции  равен …
равен …

| 
| ||

| |||

| |||

|
Решение:
Дифференциал  функции
функции  выражается формулой
выражается формулой  .
.
Тогда вычислив  , получаем
, получаем  .
.
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке

равна …

| 
| ||
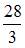
| |||

| |||

|
Решение:
Площадь данной фигуры можно вычислить по формуле  , где
, где  ,
,  ,
, 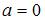 ,
, 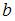 – «правая» точка пересечения параболы
– «правая» точка пересечения параболы  и прямой
и прямой  . Определим значение
. Определим значение 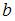 , решив уравнение
, решив уравнение  . Получаем:
. Получаем: 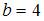 . Тогда
. Тогда 
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции 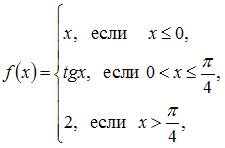 равна …
равна …

| 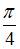
| ||
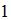
| |||
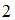
| |||
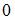
|
Решение:
Данная функция определена и непрерывна на каждом из интервалов 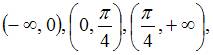 и меняет свое аналитическое выражение в точках
и меняет свое аналитическое выражение в точках 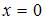 и
и 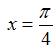 . Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
. Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Для точки 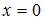 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
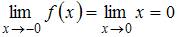 ,
,
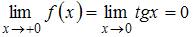 , и
, и 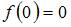 .
.
Так как 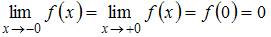 , то точка
, то точка 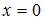 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.
Для точки 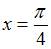 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
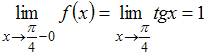 ,
,
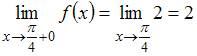 , и
, и 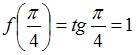 .
.
Так как 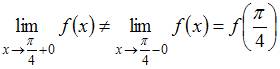 , то точка
, то точка 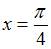 является точкой разрыва первого рода.
является точкой разрыва первого рода.
Тема: Дифференциальное исчисление ФНП
Смешанная частная производная второго порядка 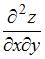 функции
функции 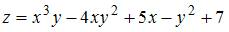 имеет вид …
имеет вид …

| 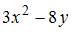
| ||

| |||

| |||

|
Решение:
При вычислении частной производной функции 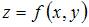 по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда

|
из
5.00
|
Обсуждение в статье: ДЕ4. Дифференциальное и интегральное исчисление |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

