Алгоритм решения парной игры с нулевой суммой

ЕН.Р.1 МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ

Практическое занятие №5 - Матричные игры

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

Направление подготовки 080500 Менеджмент

Степень (квалификация) выпускника – бакалавр менеджмента

 

 

Уфа - 2011

УДК 519.86

ББК 65.23

Л 12

 

Рекомендовано к изданию методической комиссией экономического факультета (протокол № ___ от ____________ 2011 г.)

 

 

Составитель: доцент Салимова Г. А.

 

Рецензент: ст. преподаватель кафедры информатики и ИТ Саитова Э.С.

 

 

Ответственный за выпуск:

зав.кафедрой статистики и информационных систем в экономике

к.э.н., доцент Аблеева А.М.

 

 

ОГЛАВЛЕНИЕ

 

 

Введение

1Цель и задачи…………………………………………………………... 4

2 Методика решения парной игры с нулевой суммой ………….5

2.1 Основные понятия ………………………………………………… 5

2.2 Алгоритм решения парной игры с нулевой суммой …………….5

3 Задания для самостоятельной работы……………….……..………..…8

4 Вопросы для самоконтроля…………………………….…………… ….11

Библиографический список…………………………….……………..…12

 

 

ВВЕДЕНИЕ

На практике часто возникают ситуации, в которых два (или более) участника преследуют различные цели. Простейшими примерами таких ситуаций являются спортивные игры, арбитражные споры, военные учения и т.д. Здесь каждый из участников сознательно стремится добиться наилучшего результата за счет другого участника.

Несовпадение целей участников процесса, их интересов создает конфликт между ними, или конфликтную ситуацию. Необходимость анализировать такие ситуации привела к возникновению раздела прикладной математики по названием «теория игр», в котором изучаются конфликтные ситуации на основе их математических моделей. При этом следует отметить, что методы и рекомендации теории игр разрабатываются применительно к многократно повторяющимся ситуациям. Для конфликтных ситуаций, реализующихся однократно или ограниченное число раз, рекомендации тории игр теряют смысл.

Чтобы проанализировать конфликтную ситуацию, строится ее математическая модель, в которой учитываются лишь важнейшие факторы, которые существенно влияют на ход конфликта.

 

 

ЦЕЛЬ И ЗАДАЧИ

Цель: Освоить методику решения парных игр с нулевой суммой

Задачи: 1 Усвоить алгоритм решения парной игры с нулевой суммой.

2 Научиться определять верхнюю и нижнюю цену игры.

3 Научиться решать игры в чистых стратегиях.

4 Решать экономические задачи методами теории игр.

5 Проводить анализ полученного решения.

 

 

2 МЕТОДИКА РЕШЕНИЯ ПАРНОЙ ИГРЫ С НУЛЕВОЙ СУММОЙ

Основные понятия

Парные игры – это игры с двумя игроками. В зависимости от числа стратегий различают конечные и бесконечные игры. Мы будем рассматривать лишь конечные игры, в которых каждый игрок располагает конечным числом возможных стратегий. Стратегией игры называется совокупность правил, определяющих поведение игрока от начала игры до ее завершения. Стратегии каждого игрока определяют результаты или платежи в игре. Игра называется игрой с нулевой суммой, если проигрыш одного игрока равен выигрышу другого. Результаты конечной парной игры с нулевой суммой можно задавать матрицей, строки и столбцы которой соответствуют различным стратегиям, а ее элементы – выигрышам одной стороны (равные проигрышам другой). Эта матрица называется платежной матрицей, или матрицей игры.

Если первый игрок имеет mстратегий, а второй – n стратегий, то говорят, что мы имеем дело с игрой m x n. Если игроку предоставлен выбор одной единственной стратегии, то говорят, что игрок выбирает “чистую“ стратегию. То есть, чистыми называют стратегии, соответствующие некоторой одной строке платежной матрицы или некоторому одному столбцу.

Решить игру – это значит определить наилучшую (оптимальную) стратегию каждого игрока и цену игры.

Для решения игры двух лиц с нулевой суммой используется критерий минимакса-максимина.

Алгоритм решения парной игры с нулевой суммой

 

Задача 1. Дана платежная матрица 3 х 4, которая определяет выигрыш первого игрока.

10 4 11 7

А = | а_ij | = 7 6 8 20 .

6 2 1 11

 

Определить оптимальные стратегии игроков и цену игры.

Последовательность решения задачи.

1 Представим игру в виде таблицы:

 

Стратегии Игрока I	Стратегии игрока II	Значение, α ј	α
В1	В2	В3	В4
А1						-
А2
А3						-
Значение βі					-	-
Β	-		-	-	-	-

 

2 Проанализируем последовательно каждую стратегию игрока 1. Если игрок 1 выбирает стратегию А₁, он может получить выигрыш в размере 10, 4, 11, 7 единиц в зависимости от выбранной стратегии игроком II. При этом выигрыш игрока будут не меньше:

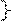
α ₁ = min 10, 4, 11, 7 = 4 ед.

независимо от поведения игрока 2.

Аналогично, при выборе игроком 1 стратегии А₂ гарантированный выигрыш будет равен:

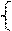α ₂ = min 7, 6, 8, 20 = 6 ед.

При выборе игроком 1 стратегии А₃ гарантированный выигрыш его будет равен

α ₃ = min 6, 2, 1, 11 = 1 ед

 

Затем из всех α _i = 4, 6, 1 игрок I выделяет наибольшее α = max α _i ,

i

т.е. в данном случае число 6, и выбирает соответствующую ему чистую стратегию А2. Ее называют максиминной, поскольку она отвечает величине

 

α = max min α _{i j} . ( 1 )

i j

Число α , определяемое по формуле ( 1 ), называется нижней чистой ценой игры (максимином). Оно показывает, какой минимальный выигрыш может получить игрок I, правильно применяя свои чистые стратегии при любых действиях игрока II.

В свою очередь, игрок II, стремясь минимизировать проигрыш, использует принцип: сначала для каждой чистой стратегии В_j ( j = 1,2,3,4) найдет максимально возможный проигрыш β_j = max α _{i j} ( j = 1,2,3,4), т.е.

I

для стратегии В₁: β₁ = max 10, 7, 6 = 10,

В₂: β₂ = max 4, 6, 2 = 6,

В₃: β₃ = max 11, 8, 1 = 11,

 

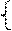В₄: β₄ = max 7, 20, 11 = 20.

 

Затем среди β_j ( j = 1,2,3,4) выберет минимальное значение β = min β_j:

j

β = min (10, 6, 11, 20 ) = 6,

 

которому будет соответствовать чистая стратегия В2. Ее называют минимаксной, так как она соответствует величине

 

β = min max β _{i j .} (2)

j i

 

Число β, определяемое по формуле (2), называется верхней чистой ценой игры (минимаксом). Оно показывает, какой максимальный проигрыш может быть у игрока II, при правильном выборе им своих чистых стратегий независимо от действий игрока 1.

Таким образом, решением игры будет: выбор игроком I стратегии А2, выбор игроком II стратегии В2, цена игры равна υ = α = β = 6.

Теорема 1 (без доказательства). В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т.е. α < β.

Если в матричной игре нижняя и верхняя чистые цены совпадают, т.е. α = β,тоговорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры υ = α = β.