Теорема о дифференцировании суммы, произведении, частного (доказать для суммы)

Производная алгебраической суммы функций

выражается следующей теоремой.

Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)' = u'±v'

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

(u — v + w)' = u' — v' + w'

Производную произведения функций определяет

Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

(uv)' = u'v + uv'

Следствие 1. Постоянный множитель можно выносить за знак производной (cv)' = cv' (с = const).

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.

Например, (uvw)' = u'vw + uv'w + uvw'

Производная частного двух функций

выражается следующей теоремой.

Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

Сформулировать теорему о дифференцировании обратной функции

Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

Доказательство

Пусть - дифференцируемая функция, .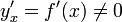
Пусть - приращение независимой переменной y и - соответствующее приращение обратной функции .
Напишем тождество

Переходя в этом равенстве к пределу при , которое влечет за собой стремление к нулю ( ), получим:

, где - производная обратной функции.

5. Сформулировать теорему о дифференцировании сложной функции.

Пусть функция z = f(x, y) дифференцируема в точке (x₀, y₀) и ее аргументы x = x(t) и y = y(t) дифференцируемы в точке t₀ , причем x(t₀) = x₀ , y(t₀) = y₀ .

Тогда сложная функция z = f(x(t), y(t)) переменной t дифференцируема в точке t₀ и ее производная вычисляется по формуле

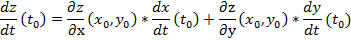
6. Дифференцирование основных элементарных функций.