Производная и дифференциал

Определения производной и дифференциала функции комплексного переменного дословно совпадают с соответствующими определениями для функции одного действительного переменного. Пусть w=f(z)=u+iv определена в некоторой окрестности U точки z₀. Дадим независимой переменной z=x+iv приращение ∆z=∆x+i∆y , не выходящее за пределы окрестности U. Тогда соответствующая функция w=f(z). получит соответствующее приращение ∆w=f(z₀+∆z)-f(z₀). Производной функции w=f(z) в точке z₀ называется предел отношения приращения функции ∆w к приращению аргумента ∆z при ∆z->0. Производная обозначается f'(z), w', dw/dz и т.д. Определение производной можно записать в виде

Предел (1) может и не существовать тогда говорят , что функция w=f(z) не имеет в точке z₀ производной. Функция w=f(z) называется дифференцируемой в точке z₀ если она определена в некоторой окрестности U точки z₀ и ее приращение ∆w можно представить в виде:

∆w=A∆z+α(∆z)_*∆z (2)

где число А не зависит от ∆z, а α(∆z)-бесконечно малая функция ∆z->0. Выражение f'(z)∆z называется дифференциалом переменного z и обозначается dz . Т.о образом dw=df(z₀)=f'(z₀)dz. Дифференциал есть главная линейная часть приращения функции.

Функция u=u(x,y) действительных переменных х и у называется дифференциалом в точке Р₀(х₀,у₀), если она определена в некоторой окрестности т. Р₀ и ее полное приращение ∆u=u(x₀+∆x,y₀+∆y)-u(x₀,y₀) представлено в виде

∆u=B∆x+C∆y+β(∆x,∆y)∆x+γ(∆x,∆y)∆y (3)

где В и С -действительные числа , независящие от ∆x и ∆y, а β и γ- действительные функции переменных ∆x и ∆y стремящиеся к 0 при ∆x->0 и ∆y->0. Если функция u дифференцируема в точке Р₀ то она имеет частные производные в Р₀, причем

но, в отличие от функции одного переменного из существования частных производных функции u(x,y) еще не следует ее дифференцруемость.

Условия Коши-Римана.

Теорема1:Пусть функция комплексно переменного w=f(z)=u(x,y)+iv(x,y) определена в окрестности т. z₀=x₀+iy₀. Для того чтобы f(z) была диффер-мой в т. z₀ необходимо и достаточно, чтобы функции u(x,y) и v(x,y) были дифф-мы в т. (x₀+y₀) и чтобы в этой точке выполнялись условия :

Равенства (1) называются условиями Коши-Римана.

Док-во: Необход.. Пусть функция w=f(z) диффер-ма в точке z₀ т.е. ∆w=∆u+i∆v=f'(z₀)∆z+α(∆z)∆z (2).

Обозначим f'(z₀)=a+ib ; α(∆z)=β(∆x,∆y)+iγ(∆x,∆y), ∆z=∆x+i∆y, где β и γ-действ-ые функции переменных х и у , стремятся к 0 при ∆x-> u ∆y->0. Подставляя эти равенства в (5) и выделяя действительные и мнимые части , получим: ∆u+i∆v=(a+ib)(∆x+i∆y)+(β(∆x,∆y)+iγ(∆x,∆y))(∆x+i∆y)=

=(a∆x-b∆y+β(∆x,∆y)∆x-γ(∆x,∆y)∆y)+

+i(b∆x+a∆y+β(∆x,∆y)∆y+γ(∆x,∆y)∆x) (3)

Поскольку равенство компл. чисел равносильно равенству их действ. И мнимых частей, то (3) равносильно системе равенств:

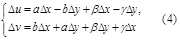
Равенства (3) означают, что функции u(x,y), v(x,y) удовлетворяют условию

∆u=B∆x+C∆y+β(∆x,∆y)∆x+γ(∆x,∆y)∆y, и следовательно, являются диффер-ми, т.к. коэффициент при ∆x и ∆у равны частным производным по х и у соответственно, то из (3) получаем:

a=∂u/∂x ; -b=∂u/∂y ; b=∂v/∂x ; a=∂v/∂y (4)

Отсюда и следует условие (1).

Достаточность. Предположим теперь, что функции u(x,y) и v(x,y) дифференцируемы в точке (х₀,у₀) и выполнены условия (1). Обозначая

a=∂u/∂x ; -b=∂u/∂y и применяя (1) придем к равенствам (4) .Из (4) и условия диффер-сти функций u(x,y) и v(x,y) имеем:

где β₁,β₂,γ₁,γ₂-функции стремящиеся к 0 при ∆x->0 ∆у->0 Отсюда

∆u+i∆v=(a+ib)(∆x+i∆y)+(β₁+iβ₂)∆x+(γ₁+iγ₂)∆у (5)

Определим функцию α(∆z) равенством:

α(∆z)=[(β₁+iβ₂)∆x+(γ₁+iγ₂)∆у]/∆z и положим А=a+ib, тогда (5) перепишется в виде ∆w=∆u+i∆v=A∆z+α(∆z)∆z, которое совпадает с (2). Для доказательства дифференцируемости f(z) осталось показать, что

lim α(∆z)=0 (при ∆z->0). Из равенства |∆z|=√(∆x)²+(∆y)² следует, что |∆х|≤|∆z|, |∆у|≤|∆z| поэтому |α(∆z)|

|α(∆z)|≤(|β₁+iβ₂||∆z|+|γ₁+iγ₂||∆z|/|∆z|)=|β₁+iβ₂|+|γ₁+iγ₂|

при ∆z->0, ∆х->0 и ∆у->0 ,а значит и функции β₁,β₂,γ₁,γ₂

стремятся к 0 , поэтому α(∆z)->0 при ∆z->0, что и требовалось доказать.