 |
Главная |
Криволинейный интеграл
|
из
5.00
|
— интеграл, вычисляемый вдоль какой-либо кривой на плоскости или в пространстве. Утверждения в этой статье приведены для пространства  , но могут быть обобщены на пространство произвольной размерности.
, но могут быть обобщены на пространство произвольной размерности.
Пусть  — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.
— гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.

 — (отрезок параметризации) — рассматриваем часть кривой.
— (отрезок параметризации) — рассматриваем часть кривой.
Пусть  — разбиение отрезка параметризации
— разбиение отрезка параметризации 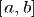 , причем
, причем  .
.
Зададим разбиение кривой  .
.
За 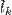 обозначим часть кривой от точки
обозначим часть кривой от точки  до точки
до точки  ,
,  .
.
Введем мелкость разбиения отрезка параметризации 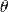 :
:  .
.
Введем набор промежуточных точек разбиения отрезка параметризации  :
:  .
.
Зададим набор промежуточных точек разбиения кривой 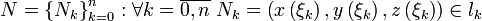 .
.
Пусть нам также даны 4 функции, которые определены вдоль кривой  :
:  ,
,  ,
,  ,
, 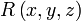 .
.
Рассмотрим 4 интегральные суммы.
1. Интегральная сумма криволинейного интеграла первого рода:
 .
.
1. Три интегральных суммы криволинейного интеграла второго рода:
 ,
,
 ,
,
 .
.
Если  , то говорят, что функция
, то говорят, что функция 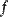 интегрируема в смысле криволинейного интеграла первого рода по кривой
интегрируема в смысле криволинейного интеграла первого рода по кривой  , а сам предел называют криволинейным интегралом первого рода функции
, а сам предел называют криволинейным интегралом первого рода функции 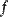 по кривой
по кривой  и обозначают
и обозначают 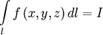 . Здесь
. Здесь  — дифференциал кривой.
— дифференциал кривой.
Если  ,
,  ,
,  , то говорят, что функции
, то говорят, что функции 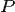 ,
,  и
и  интегрируемы в смысле криволинейного интеграла второго рода по кривой
интегрируемы в смысле криволинейного интеграла второго рода по кривой  , а сами пределы называют криволинейными интегралами второго рода функций
, а сами пределы называют криволинейными интегралами второго рода функций 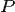 ,
,  и
и  по кривой
по кривой  и обозначают
и обозначают


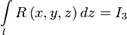
Сумму криволинейных интегралов второго рода функций  ,
,  и
и  также называют криволинейным интегралом второго рода вектор-функции
также называют криволинейным интегралом второго рода вектор-функции  и обозначают:
и обозначают:
 .
.
Если кривая  замкнута (начало совпадает с концом), то в этом случае вместо значка
замкнута (начало совпадает с концом), то в этом случае вместо значка  принято писать
принято писать  .
.
Точка ветвления или особая точка многозначного характера— особая точка полной аналитической функции, такая, что аналитическое продолжение какого-либо элемента этой функции вдоль замкнутого пути, охватывающего эту точку, приводит к новым элементам этой функции.
Точки ветвления могут быть разделены на две категории:
1. Если при  –кратном обходе указанного пути мы вновь получим исходный элемент, тогда данная точка называется точкой ветвления конечного порядка (а именно порядка
–кратном обходе указанного пути мы вновь получим исходный элемент, тогда данная точка называется точкой ветвления конечного порядка (а именно порядка  );
);
2. Если такого не происходит, то точка будет точкой ветвления бесконечного порядка или логарифмической точкой ветвления
Из теоремы Пуанкаре — Вольтерры прямо следует, что данными двумя случаями варианты точек ветвления исчерпываются.
Формула Коши
 Пусть функция
Пусть функция  аналитическая в односвязной замкнутой области
аналитическая в односвязной замкнутой области 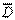 (
(  ), с кусочно-гладкой границей
), с кусочно-гладкой границей  , ориентированной в положительном направлении (рис. 142), т. е. против часовой стрелки. Тогда имеет место формула Коши
, ориентированной в положительном направлении (рис. 142), т. е. против часовой стрелки. Тогда имеет место формула Коши
,
где  - любая точка внутри контура
- любая точка внутри контура  .
.
Таким образом, аналитическую функцию достаточно определить на контуре  , а по формуле (1) можно автоматически получить ее значения в других точках
, а по формуле (1) можно автоматически получить ее значения в других точках  .
.
|
из
5.00
|
Обсуждение в статье: Криволинейный интеграл |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

