Тема №15. Геометрическое решение задач линейного программирования

Неравенство называется линейным, если оно содержит переменные только в первой степени, причем существуют произведения переменных.

В общем виде линейное неравенство с двумя переменнымизаписывается следующим образом:

(1) aх₁ + bx₂ + с или

(2) ах₁ + bx₂ + с

Каждому решению неравенства, т.е. паре чисел (х₁; х₂) ,

соответствует точка на плоскости.

Геометрический смысл:

Множеством решений линейного неравенства (1) служит одна из двух полуплоскостей, на которые всю плоскость делит прямая ах₁ + Ьх₂ + с = 0, включая и эту прямую, а другая полуплоскость вместе с той же прямой является множеством решений неравенства (2) .

1. Построить множества решений неравенства

3x₁ + 4х₂ - 12 0

Строим прямую 3x₁ + 4х₂ - 12 = 0 по точкам пересечения ее с осями координат: (0; 3) и

(4; 0}.

Для решения строгого неравенства 3x₁+ 4х₂ - 12 > 0 берем точку (0; 0):

3 * 0 + 4 * 0 - 12 > 0, -12 > 0 - не верно => нижняя полуплоскость не может служить множеством решений => решением данного неравенства служит верхняя полуплоскость, содержащая прямую АВ (т.к. знак ).

Пример2.

Построить множество решений системы линейных неравенств

Найдём координаты угловых точек:

1) Строим прямую х₁ + х₂ - 3 = 0 по точкам (0; 3) и (3; 0) ,
подставляем контрольную точку (0; 0), получаем верное неравенство -3 < 0 => множеством решений данного неравенства является полуплоскость, содержащая начало координат вместе с прямой АВ.

2) Строим прямуюх₁ + х₂ - 1 = 0 по точкам (0; 1) и

(1; 0),

в точке (0; 0) получаем неверное неравенство

-1 > 0 => множеством решений является верхняя полуплоскость.

Решением двух первых неравенств является неограниченная полоса между I и II прямыми.

3) Строим прямуюх₁ - х₂ = 0. Для нахождения полуплоскости
решений строгого неравенства х₁ - х₂ > 0 в качестве контрольной точки возьмем (0; 2); 0 - 2 > 0 - не верно => множеством решений служит нижняя полуплоскость.

Множеством решений системы из трех неравенств является неограниченная часть области между параллельными прямыми, расположенная ниже прямой III.

4) Строим прямую х₁ = 2,5. Значения х₁ < 2,5 лежат левее
этой прямой, что и определяет множество решений данного неравенства.

Множеством решений системы из четырех неравенств является выпуклый многоугольник EKBL.

5) Двойное неравенство эквивалентно системе двух

неравенств х₂ 0 и х₂ 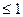. Неравенству х₂ 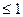соответствует полуплоскость, расположенная ниже прямой х₂ = 1. Неравенству х₂ соответствует полуплоскость, лежащая выше оси абсцисс.

Множество решений системы из всех пяти неравенств - выпуклый многоугольник ABCDEF.

Координаты угловых точек найдем как координаты точек пересечения прямых:

Геометрический метод решения задачи линейного программирования имеет такие узкие рамки применения, что о нем как об особом методе решения говорить нельзя. Однако он позволяет выработать наглядное представление о задачах линейного программированияи геометрически подтвердить основные теоремы линейного программирования.

Требуется найти такую точку этого многоугольника, которая бы максимизировала линейную форму

F = х₁ - х₂. Как располагаются на плоскости точки, в которых функция F принимает одно и то же значение? Для ответа на этот вопрос достаточно форму F приравнять какой-то постоянной величине, т.е. F = const = a. Это приводит куравнению х₁ - х₂ = а, которое является уравнением прямой на плоскости. Меняя значение а, получим семейство параллельных прямых. Каждая из этих прямых называется линией уровня.

На рисунке построена линия xl - х2 = 0, котораясоответствует значению

F = 0. При переходе от одной линии уровня к другойзначение функции F изменяется (нужно найти max) .

Нужное направление движения исходной линии уровня можно установить следующим образом. Найдем координаты нормального вектора (l; -1} . Из рисунка видно, что значения функции F возрастают при перемещении исходной линии уровня в направлении вектора .

Если бы требовалось найти minфункции F, то исходную линию уровня следовало бы передвигать в сторону, противоположную вектору .

Для простоты построения исходной линии уровня за величину a можно взять произведение коэффициентов при переменных в выражении функцииF или величину, кратнуюэтому произведению.

Итак, будем передвигать прямую в направлении вектора . Максимальное значение линейной формы в многоугольнике OABCD будет достигнуто в угловойточке С, а далее линия уровня выйдет за пределы многоугольника. Подставим координаты точки С (6; 2) в выражение F и найдем max значение функции:

F = 6 - 2 = 4

Таким образом мы показали, что линейная форма достигает max значения вугловой точке многоугольника решений.