 |
Главная |
Тема №16.Решение задач линейного программирования
|
из
5.00
|
Симплекс-метод является универсальным методом, которым можно решить любую задачу линейного программирования, используя систему ограничений, приведенную к общему виду, т.е. систему m линейных уравнений n - неизвестный (m<n), находят любое ее базисное решение, по возможности более простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплекс-метод гарантирует, что при этом новом решении линейная форма, если и не достигает оптимума, то приблизится к нему и т.д. Если же первое найденное базисное решение окажется недопустимым, то с помощью симплекс-метода осуществляется переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком то шаге не получится допустимое базисное решение.
Т.о. применение симплекс-метода распадается на 2 этапа:
- нахождение допустимого базисного решения системы ограничений;
- нахождение оптимального решения.
Задача об использовании сырья
Для изготовления шкафов и буфетов деревообрабатывающий завод применяет древесину 4 видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 единиц.
| Виды древесины | Запасы древесины | Количество единиц древесины, необходимого для производства единицы продукции | |
| шкафы | буфеты | ||
| Прибыль |
Требуется составить такой план выпуска продукции, который бы обеспечил предприятию наибольшую прибыль от реализации всей продукции.
Решение:
Составим математическую модель. Пусть  и
и  - количество шкафов и буфетов, запланированных к производству. Т.к. количество древесины ограничено по каждому виду, то должны выполняться неравенства:
- количество шкафов и буфетов, запланированных к производству. Т.к. количество древесины ограничено по каждому виду, то должны выполняться неравенства:


Целевая функция (линейная форма), выражающая прибыль имеет вид 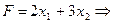
Задача сводится к нахождению max функций F при заданных ограничениях.
Сведем систему ограничений неравенств к системе уравнений, прибавив к левой части каждого неравенства добавочные неотрицательные переменные  ,
,  ,
,  ,
,  .
.
В условиях каждой задачи они имеют конкретное экономическое содержание. В данной задаче они выражают остаток древесины каждого вида после выполнения плана по выпуску продукции.

 (i=1,6)
(i=1,6)
Необходимо найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало минимальную форму 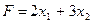 .
.
Т.к. система состоит из 4-х независимых уравнений с 6-ю переменными, то число основных переменных должно равняться 4, а число неосновных - 2.
Нужно найти любое базисное решение. Для этого достаточно взять в качестве основных добавочные переменные  ,
,  ,
,  ,
,  . Т.к. коэффициент при этих переменных образуют единичную матрицу, то отпадает необходимость проверять определитель. Полагая
. Т.к. коэффициент при этих переменных образуют единичную матрицу, то отпадает необходимость проверять определитель. Полагая 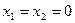 , получим базисное решение. (0;0;120;160;120;80), оно оказалось и допустимым. Переходим ко 2-му этапу симплекс-метода.
, получим базисное решение. (0;0;120;160;120;80), оно оказалось и допустимым. Переходим ко 2-му этапу симплекс-метода.
I. Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
, 
В системе выразим основные переменные через неосновные. Линейную форму тоже выразим через неосновные переменные.

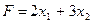
При 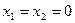 имеет
имеет  , что совпадает с базисным решением (0;0;120;160;120;80). При этом базисном решении
, что совпадает с базисным решением (0;0;120;160;120;80). При этом базисном решении  .
.
Когда мы полагаем 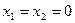 (завод ничего не выпускает) была поставлена цель - найти первые, безразлично какое, базисное решение. Цель достигнута. Теперь необходимо перейти к другому решению, при котором значение F увеличится.
(завод ничего не выпускает) была поставлена цель - найти первые, безразлично какое, базисное решение. Цель достигнута. Теперь необходимо перейти к другому решению, при котором значение F увеличится.
Из линейной формы видно, что ее значение увеличивается при увеличении  и
и  их невыгодно считать неосновными. Их нужноперевести в число основных. Это означает переход к новому базисному решению. При симплекс-методе на каждом шаге предполагается перевод в число основных только одной из свободных переменных.
их невыгодно считать неосновными. Их нужноперевести в число основных. Это означает переход к новому базисному решению. При симплекс-методе на каждом шаге предполагается перевод в число основных только одной из свободных переменных.
Переведем в число основных  , т.к. коэффициент при ней больше, но тогда в число неосновных тоже необходимо перевести переменную.
, т.к. коэффициент при ней больше, но тогда в число неосновных тоже необходимо перевести переменную.
Значение  необходимо сделать, как можно большим. Однако, оказывается, что увеличение
необходимо сделать, как можно большим. Однако, оказывается, что увеличение  может продолжаться только до известных границ. Так из 1-го уравнения системы следует, что
может продолжаться только до известных границ. Так из 1-го уравнения системы следует, что  , т.к. только при этих значениях
, т.к. только при этих значениях  остается положительной. Из 3-го уравнения системы следует, что
остается положительной. Из 3-го уравнения системы следует, что  , т.к. только при этих значениях
, т.к. только при этих значениях  остается положительным. Из 4-го следует
остается положительным. Из 4-го следует 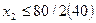 , т.к. только при этих значениях
, т.к. только при этих значениях  положительно. Всем этим условиям удовлетворяет
положительно. Всем этим условиям удовлетворяет  - это I уравнение системы.
- это I уравнение системы.
Т.о. для ответа на вопрос, какую переменную нужно перевести в число неосновных, нужно принять  , при этом значение
, при этом значение 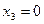 и следовательно
и следовательно  переходит в число неосновных, а
переходит в число неосновных, а  ,
,  остаются положительными.
остаются положительными.
II Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные :  ,
,  .
.
Выразим основные переменные и линейную форму через неосновные. В системе берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при  .
.
В данном случае это I уравнение системы


При  F=90. Это уже лучше, но не искомый max, т.к. F можно еще увеличить за счет
F=90. Это уже лучше, но не искомый max, т.к. F можно еще увеличить за счет  . Переводим
. Переводим  в число основных и определяем какую переменную перевести в неосновные. Находим
в число основных и определяем какую переменную перевести в неосновные. Находим  , тогда
, тогда  и
и  переходит в число неосновных - это последнее уравнение системы.
переходит в число неосновных - это последнее уравнение системы.
III Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  .
.
Выражаем основные переменные через линейную форму через неосновные, начиная с последнего уравнения (т.к. оно дало min  ).
).


Из вида линейной формы следует, что ее max значение еще не получено, т.к. возможно ее увеличение за счет  .
.
Находим 
Получим 2 положения, которые необходимо разъяснить:
1)  входит в выражение для
входит в выражение для  (I уравнение), но имеет положительный коэффициент, следовательно, при любом возрастании
(I уравнение), но имеет положительный коэффициент, следовательно, при любом возрастании  переменная
переменная  не может стать отрицательной, следовательно, никаких ограничений на возрастание
не может стать отрицательной, следовательно, никаких ограничений на возрастание  не накладывается, поэтому будем писать
не накладывается, поэтому будем писать 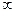 .
.
2) Получились 2 минимальных значения, равные 40.
Если  =40, то
=40, то 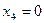 и
и  .
.
Но обе переменные нельзя переводить в число неосновных, но число основных не должно быть <4-х. Тогда одну переменную оставляют в числе основных (  ) и считают ее значение =0, т.е. базисное решение оказывается вырожденным. А другую переводят в число неосновных (
) и считают ее значение =0, т.е. базисное решение оказывается вырожденным. А другую переводят в число неосновных (  ) (последнее уравнение).
) (последнее уравнение).
IV Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  .
.
Выражаем основные переменные и линейную форму через неосновные (начиная с последнего уравнения).


Т.к.  и
и  входят в линейную форму с отрицательным коэффициентом, следовательно, больше не достигнуть.
входят в линейную форму с отрицательным коэффициентом, следовательно, больше не достигнуть.
Отсутствие на каком-то шаге симплекс-метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с
положительными коэффициентами является критерием оптимальности.
Итак, оптимальным служит решение (план) (40;20;40;0;0;0) при котором Fmax=140, следовательно, для получения наибольшей прибыли, равной 140 ден.ед., из данных запасов древесины завод должен изготовить 40 шкафов, 20 буфетов. При этом древесина 2,3,4 видов окажутся, использована полностью, а 40 единиц древесины 1 вида останутся неизрасходованными.
II
Остановимся более подробно на I этапе симплекс-метода. Т.е. на нахождении допустимого базисного решения. В предыдущей задаче это решение сразу было найдено и вопрос стоял только об оптимизации. При нахождении дополнительного базисного решения линейная форма в расчет не берется, и преобразования относятся только к системе ограничений.
Пусть задана задача линейного программирования в общем виде (m<n). Выберем группу m основных переменных, которые позволяют найти исходное базисное решение. Пусть основными будут первые m переменных. Выразим основные переменные через неосновные.
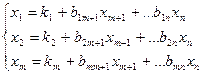
Тогда базисное решение  . Пусть это решение недопустимое, тогда необходимо перейти к допустимому решению, причем необязательно, что переход получится за 1 шаг.
. Пусть это решение недопустимое, тогда необходимо перейти к допустимому решению, причем необязательно, что переход получится за 1 шаг.
Пусть отрицательным является свободный член i-го уравнения 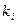 , т.е. основная переменная
, т.е. основная переменная 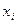 в этом базисном решении отрицательна.
в этом базисном решении отрицательна.
Для перехода к новому базисному решению необходимо решить 2 вопроса:
1) установить, какая неосновная переменная должна быть переведена в число основных.
2) выбрать переменную, которую из основных следует перевести в неосновные.
Для решения вопроса о том, какие неосновные переменные можно перевести в основные, нужно уметь находить неосновные переменные, при увеличении которых возрастает основная переменная отрицательная в исходном базисном решении.
Вернемся к i-му уравнению системы  , где
, где 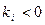 .
.
Переменная 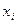 возрастает при возрастании тех неосновных переменных, коэффициенты которых в этом уравнении положительны
возрастает при возрастании тех неосновных переменных, коэффициенты которых в этом уравнении положительны  в основные можно переводить те неосновные переменные, которые в уравнении системы с отрицательным свободным членом имеют положительные коэффициенты.
в основные можно переводить те неосновные переменные, которые в уравнении системы с отрицательным свободным членом имеют положительные коэффициенты.
Может быть 3 случая:
1. В i-ом уравнении системы нет неосновных переменных с положительными коэффициентами. В этом случае система ограничений несовместна - она не имеет ни одного допустимого решения.
2. В i-ом уравнении имеется одна переменная, коэффициент которой положителен, а а значит именно эта переменная переводится в основные.
3. В i-ом уравнении имеется несколько переменных с положительными коэффициентами. В этом случае в основные можно переводить любые переменные.
Далее устанавливается, какая основная переменная должна быть переведена в число неосновных. Для этого используют уже известное правило: находят отношения свободных членов к коэффициентам при переменной, переводимой в основные из всех уравнений, где знаки свободных членов и указанных коэффициентов противоположны. Затем рассматривают абсолютную величину этих отношений и выбирают наименьшую.
Уравнение, из которого получено наименьшее отношение - выделяют. Выделенное уравнение показывают, какая из основных переменных должна быть переведена в неосновные. Выразив новые основные переменные через неосновные, переходят к следующему базисному решению. Если в выделенном уравнении свободный член отрицателен, то в новом базисном решении число отрицательных компонентов окажется меньше на 1, чем в исходном. Если же в выделенном уравнении свободный член положителен (или =0), то в новом базисном решении отрицательных компонентов останется столько же. Итак, получили новое базисное решение. Если оно недопустимо, то к нему применяют ту же схему. В результате через конечное число шагов получится допустимое решение. Только после этого переходят к оптимизации, что уже было рассмотрено.
Задача. Найти max 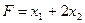 при ограничениях:
при ограничениях:

Введем добавочные неотрицательные переменные
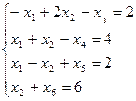
 (i=1,6)
(i=1,6)
I Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  .
.
Выражаем основные через неосновные
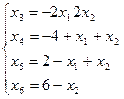
Базисное решение (0;0;-2;-4;2;6) не является допустимым. Рассматриваем уравнения с отрицательными свободными членами. В основные можно перевести  и
и  , т.к. коэффициенты при них положительны и при увеличении
, т.к. коэффициенты при них положительны и при увеличении  ,
,  ,
,  будут увеличиваться. Переведем в основные
будут увеличиваться. Переведем в основные  . Теперь встает вопрос: какую переменную переводить в неосновные. Для этого находим отношения свободных членов к коэффициентам при
. Теперь встает вопрос: какую переменную переводить в неосновные. Для этого находим отношения свободных членов к коэффициентам при  .
.
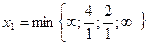 =2 - третье уравнение системы, следовательно, в неосновные переводим
=2 - третье уравнение системы, следовательно, в неосновные переводим  , но онаположительна в исходном базисном решении, а значит улучшений не получили.
, но онаположительна в исходном базисном решении, а значит улучшений не получили.
Переведем в основные  . Находим отношения
. Находим отношения  - первое уравнение - в неосновные переводим
- первое уравнение - в неосновные переводим  , которое в исходном базисном решении отрицательно.
, которое в исходном базисном решении отрицательно.
II Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  .
.

Базисное решение (0;1;0;-3;3;5) опять не является допустимым, но результат улучшился.
Рассмотрим уравнение с открытым свободным членом. В основные можно перевести  и
и  . Переведем в основные
. Переведем в основные  . Найдем
. Найдем 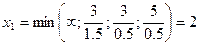 - второе уравнение, значит в неосновные переводим
- второе уравнение, значит в неосновные переводим  .
.
III Основные переменные:  ,
,  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  .
.
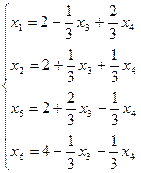
Базисное решение (2;2;0;0;2;4) - допустимое. Теперь можно приступить к оптимизации. Выражаем линейную форму через неосновные переменные 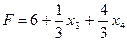 - это решение неоптимально, т.к. его можно увеличить за счет
- это решение неоптимально, т.к. его можно увеличить за счет  и
и  .
.
Переведем в основные  , имеющий больший коэффициент. Находим
, имеющий больший коэффициент. Находим  - третье уравнение - в неосновные переводим
- третье уравнение - в неосновные переводим  .
.
IV Основные:  ,
,  ,
,  ,
,  .
.
Неосновные:  ,
,  .
.
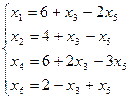

Базисное решение (6;4;0;6;0;2) не является оптимальным, т.к. F можно увеличить за счет  . Переводим
. Переводим  в основные, находим
в основные, находим  - последнее уравнение, следовательно,
- последнее уравнение, следовательно,  переводим в неосновные.
переводим в неосновные.
V Основные:  ,
,  ,
,  ,
,  .
.
Неосновные:  ,
,  .
.

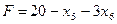
Критерий оптимальности выполнен  базисное решение (8;6;2;10;0;0) является оптимальным, а Fmax=20.
базисное решение (8;6;2;10;0;0) является оптимальным, а Fmax=20.
III
Рассмотрим упрощенную экономическую задачу, в которой требуется найти min линейной функции.
К группе задач о смесях относят задачи по отысканию наиболее дешевого набора из отпущенных исходных материалов, обеспечивающего получение смеси с заданными свойствами. Т.е. получаемые смеси должны иметь в своем составе n различных компонентов в определенных количествах, а сами компоненты являются составными частями m исходных материалов.
| Виды материалов | Цена единицы материала | Количество отдельных компонентов входящих в состав материалов | ||||
| … | j | N | ||||
| c m | 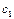
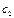
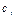

| 
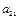
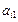
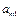
| 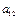


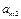
| … … … … | 
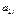
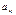
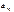
| 
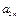
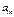

|
| Необходимое количество компонентов в смеси | 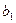
| 
| … | 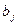
| 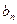
|
 показывают количество j-ой компоненты в единицы i-го материала.
показывают количество j-ой компоненты в единицы i-го материала.
Требуется получить смесь с заданными свойствами при наименьших затратах на приобретение материалов.
Обозначим через 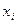 количество материала i-го вида, входящего в смесь. Тогда задача сведется к отысканию min функции:
количество материала i-го вида, входящего в смесь. Тогда задача сведется к отысканию min функции: 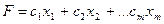 , при ограничениях:
, при ограничениях:
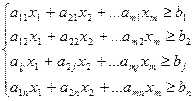
Одним из частных случаев общей задачи о смесях служит задача, о диете. Характерной особенностью такой задачи является удовлетворение потребности индивидуума в питательных веществах при наименьшей стоимости используемых продуктов.
Задача. При откорме свиней необходимо, чтобы каждая свинья получала ежедневно не менее 6 ед.вещества К, 8 ед.вещества L и 12 ед.вещества М (это могут быть жиры, белки, углеводы). Для откорма можно закупить 3 вида кормов: I, II, III (например картофель, жмых и комбикорм).
| Вид корма | Вещества | Стоимость ед. корма | ||
| K | L | M | ||
| I | ||||
| II | ||||
| III | 1,5 | 2,5 |
Требуется обеспечить наиболее дешевый рацион корма.
Пусть 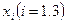 - количество единиц соответственно I, II, III видов корма. Требуется найти min линейной формы
- количество единиц соответственно I, II, III видов корма. Требуется найти min линейной формы 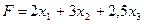 , при ограничениях:
, при ограничениях:
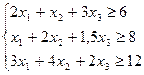
Ведем добавочные неотрицательные переменные  ,
,  ,
,  .
.
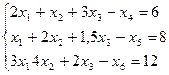
Если за основные взять добавочные переменные, то получим базисное решение
(0;0;0;-6;-8;-12), которое является недопустимым. Поэтому используем симплекс-метод для перехода к новому базисному решению.
I Основные переменные:  ,
,  ,
,  .
.
Неосновные переменные:  ,
,  ,
,  .
.
Выразим основные через неосновные.

Переведем в основные  , тогда
, тогда  при
при  =3 получаем
=3 получаем  =0
=0 
 переходит в неосновные.
переходит в неосновные.
II Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  ,
,  .
.
Выражаем  из выделенного уравнения и подставляем в остальные
из выделенного уравнения и подставляем в остальные
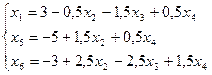
Базисное решение (3;0;0;0;-5;-3) уже лучше, чем на I шаге. Переведем в основные  , тогда
, тогда  , при
, при  =2 имеем
=2 имеем  =0
=0 
 переводим в неосновные.
переводим в неосновные.
III Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  ,
,  .
.
Выражаем из выделенного уравнения  и подставляем в остальные уравнения.
и подставляем в остальные уравнения.
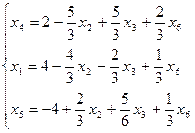
Базисное решение (4;0;0;2;-4;0) еще улучшилось. Переводим в основные  ,
, 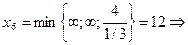 в неосновные
в неосновные  .
.
IV Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  ,
,  .
.
Выражаем, подставляем, имеем:
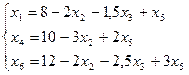
Получено базисное решение (8;0;0;10;0;12) является допустимым и первый этап симплекс-метода закончен. Переходим ко 2 этапу, будем искать оптимальное решение.
Выразим линейную форму 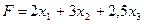 через неосновные переменные.
через неосновные переменные.
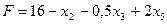 .
.
Т.к. речь идет о минимизации функции, то выгодны те переменные, которые входят в выражение линейной формы с отрицательными коэффициентами.
Переведем в основные  , тогда
, тогда 
 переходит в неосновные.
переходит в неосновные.
V Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  ,
,  .
.
Выражаем, составляем, имеем:

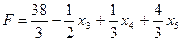
Переводим в основные  , тогда
, тогда 
 переводим в неосновные (при
переводим в неосновные (при  =8/9 имеем
=8/9 имеем  =0).
=0).
VI Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  ,
,  .
.
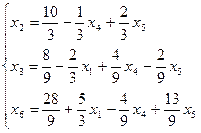
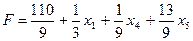
Все переменные входят в линейную форму с положительными коэффициентами, значит критерий оптимальности при отыскании минимума линейной формы выполнен.
Т.о. оптимальным служит решение (0;10/3;8/9;0;0;28/9), при этом 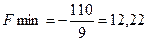 д.ед.
д.ед.
Итак, чтобы обеспечить наиболее дешевый рацион питания, нужно в основном покупать самый дорогой корм II вида, корма III вида нужно закупать почти в 4 раза меньше, а корм I вида, хотя самый дешевый, но невыгодный. При этом оптимальном решении будут обеспечены нормы веществ K и L, а вещества М окажется на 28/9 ед. больше нормы.
Во всех рассмотренных задачах системы ограничений были совместными и имелся конечный оптимум, причем единственный.
Рассмотрим частные случаи, когда эти условия нарушаются.
Пример1. Найти  , при ограничениях
, при ограничениях
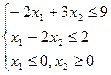
Введем добавочные переменные
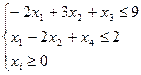 (i=1,4)
(i=1,4)
Если взять за основные  и
и  , то исходное базисное решение (0;0;9;2) допустимое.
, то исходное базисное решение (0;0;9;2) допустимое.
I Основные переменные:  ,
,  .
.
Неосновные переменные:  ,
,  .
.

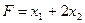 (=0)
(=0)
Переведем  в основные, тогда
в основные, тогда 
 переводим в неосновные.
переводим в неосновные.
II Основные переменные:  ,
,  .
.
Неосновные переменные:  ,
,  .
.
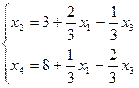
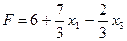
Из вида линейной формы следует, что  необходимо перевести в основные, тогда
необходимо перевести в основные, тогда 
 может возрастать неограниченно (
может возрастать неограниченно (  и
и  не станут при этом отрицательными) значит и функция F также неограниченно может возрастать, а значит
не станут при этом отрицательными) значит и функция F также неограниченно может возрастать, а значит 
Пример2. Найти максимум  при ограничениях
при ограничениях

Введем добавочные неотрицательные переменные
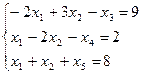
 (j=1,5)
(j=1,5)
Переменные  ,
,  ,
,  - основные, тогда базисное решение недопустимое (0;0;-9;-2;8). Используем симплекс-метод для нахождения допустимого базисного решения.
- основные, тогда базисное решение недопустимое (0;0;-9;-2;8). Используем симплекс-метод для нахождения допустимого базисного решения.
I Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  .
.

Переводим  в основные, тогда
в основные, тогда 
 переводим в неосновные
переводим в неосновные
II Основные:  ,
,  ,
,  .
.
Неосновные:  ,
,  .
.

Во 2-ом уравнении и свободный член, и все коэффициенты при неосновных переменных отрицательны - это является признаком того, что система несовместна. Она не имеет ни
|
из
5.00
|
Обсуждение в статье: Тема №16.Решение задач линейного программирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

