Матричные схемы алгоритмов (МСА)

Синтез микропрограммных

Автоматов.

МПА и их особенности.

 

 

 

МПА - управляющие автоматы, форми- рующие последовательности сигналов, инициирующих выполнение микропрог- рамм в операционных автоматах (объек-

тах управления).

 

МПА обладает рядом особенностей:

· это инициальные автоматы (имеющие начальное состояние);

· это циклические автоматы (многократно формирующие последовательность управляющих сигналов);

 

 

 

· это структурные автоматы с кодированными (как правило двоично) входным и выход-ным алфавитами, причем с достаточно большим числом входов и выходов.

 

 

 

 

Для МПА используются свои специфи-

ческие методы анализа и синтеза, так

как большое число выходов и особенно

входов затрудняет применение канони-

ческих методов.

 

 

 

МПА в простейшем случае взаимодей- ствуют с ОА только по выходам.

 

 

Здесь микропрограммы не имеют раз- ветвлений - они безусловны.

 

В общем случае МПА работает в контуре, причем не только с ОА, но и с внешней средой, выполняющей роль управления более высокого уровня. Сигналы внешней среды инициируют требуемую работу УА в зависимости от состоя-ний УА и ОА.

 

 

 

 

Микропрограммы здесь могут быть условными,

зависящими от оповещающих сигналов.

 

Обычно МПА рассматривается для контура

«УА-ОА» .В этом контуре хотя бы один из автоматов имеет задержку – является авто-

матом Мура или автоматом Мили с задерж-

кой. Микропрограммирование должно учи-тывать взаимодействие УА и ОА.

 

 

 

Рассмотрим варианты такого взаимо-

действия.

 

1. Пусть УА - автомат с задержкой, а ОА - автомат Мили (по оповещаю-щим сигналам).

 

 

 

\ Y(t+1) = j(Y(t))

Микрокоманда в такте (t+1) зависит от результатов микрокоманды такта t.

 

 

2. 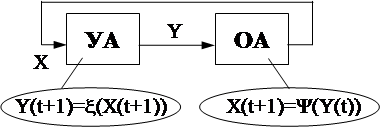УА - автомат Мили.
ОА - автомат с задержкой

 

 

\ Y(t+1) = j(Y(t)). Микрокоманда в такте (t+1) зависит от результатов микрокоманды такта t.

3. УА и ОА оба с задержкой

 

\ Y(t+2) = j(Y(t))

Микрокоманда в такте (t+2) зависит от результатов микрокоманды такта t.

 

 

Чаще всего УА строятся как автоматы с

задержкой , а ОА - как автоматы Мили

(по оповещающим сигналам).

 

 

 

Граф- схемы алгоритмов (ГСА)

 

 

См. методичку

Першеев В.Г. «Построение МПА»,

раздел 2

 

 

 

 

 

 

Матричные схемы алгоритмов (МСА)

 

 

См. методичку

Першеев В.Г. «Построение МПА», раздел 3

 

x1

x2

Кн

y1 y2

y2

y2

 

y1

К1

 

К2

 

 

К3

 

К4

 

МСА по строкам описывается формулами переходов.

Продолжение примера.

Кн®К₁

К₁®x₁K₂ Ú ₁x₂К₃ Ú _{1 2}К₄

К₂®К₃

.

.

.

 

 

Формулы переходов МСА обязательно ортогональны (условия переходов к раз-

ным столбцам несовместимы)

К_i® ₁К_j Úx₂К_p Ú...

 

Если МСА полностью определена, все ее формулы переходов полны: дизъюнкция

условий по строке (любой) равна 1.

 

 

Переходя от ГСА к МСА , мы получаем полностью определенную МСА . Недоопределенной МСА соответствует фраг-

мент ГСА (часть вершин такого фрагмента не будет иметь связей).