Пример построения автома- та Мили по МСА с миними- зацией числа состояний

 

Пусть ОУ имеет вид:

 

 

p₁p₂ = 11 задает алгоритм А₁.

p₁p₂ = 10 задает алгоритм А₂.

p₁p₂ = 00 задает ожидание инициирова-

337 ния работы (алгоритм А₃).

Влияние микроопераций на значение x таково:

y₁,y₂ - не меняет x

y₃ - устанавливает x любым

y₄ - устанавливает x = 1

 

Значения p₁p₂ не меняются во время ра- боты УА по частному алгоритму.

 

 

 

		Частные МСА

 

кк

К6

К5

К4

К3

К1

ОМСА

К2

p1p2 p1p2x p1p2x p1p2 p1p2 p1p2 p1p2;p1p2 p1p2 p1p2 p1p2

Кнн

К1

К2

К3

К4

К5

К6

p1p2 p1p2 p1 p1p2x p1p2x p1p2

j

p1p2 p1p2x p1 p1p2x p1p2x p1p2

y

341

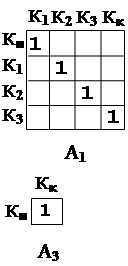Полученные y_i подставляем в МСА, что дает:

 

 

 

Повторные получения y_i и их подстанов-

ки дают такую же МСА и процесс уточ- нения заканчивается.

По этой МСА строим автомат, отмечая

как S₀ К_н, К_к, а также К₃ и К₆, так как от них есть переход только к К_к (См. 3.9).

 

 

После минимизации имеем

 

 

Упростив условия переходов, получаем

 

Синтез схем МПА

 

Схемы с дешифраци- ей состояний.

 

 

 

См. методическое пособие

Каган Б.М., Першеев В.Г. "Синтез МПА",

раздел 2.

 

Будем строить схему по обратной структурной таблице (ОСТ) автомата, являющейся расшире-

нием ОТП и имеющей формат вида:

 

1 2 3 4 5 6 7

j - сигналы возбуждения ЭА.

 

 

 

Сначала из ОТП в ОСТ заносим содер-

жимое колонок 1,3,4 и 6. Далее, закоди-

ровав состояния МПА, заполним колон-

ки 2 и 5 и в 7 заносим имена сигналов j, требующих единичного значения для обеспечения перехода из S_исх в S_пер (по матрицам переходов ЭА).

 

 

Затем выписываем для каждого имени из 6 и 7 условия их единичных значений, то- есть функ-ции выходов и возбуждения. При этом S_исх пред-ставляются своими именами, а не через состоя-ния ЭА.

 

 

Далее строится схема вида:

 

 

Пример

Возьмем МПА из 3.14 и опишем ОСТ.

В качестве ЭА выберем триггеры типа D.

Состояния Q₂Q₁ 00, 01, 10 примем для кодов S₀, S₁, S₂.

 

 

ОСТ имеет вид

 

 

 

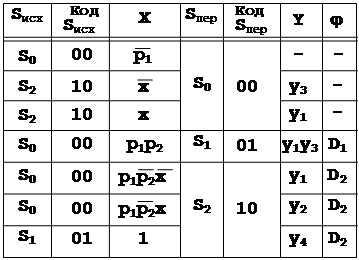Из ОСТ выписываем:

 

 

Далее рассмотрим схему.

 

 

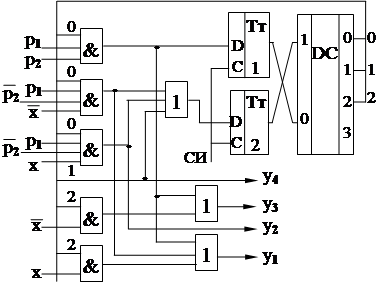
Выделение как отдельной схемы дешифратора упрощает реализацию j и Y, так как в нем сконцентрированы общие повторяющиеся части конъюнкций (для кодов S) функций выходов и возбуждения.

МПА Мура строится аналогично. При этом

функцию выходов в ОСТ удобнее заносить

(а затем выписывать из ОСТ ), считая

аргументом для Y значение S_пер , что дает

более простую форму для записи Y = F(S).

Схема с дешифрацией состояний может упростится при неполной дешифрации

состояний.

При этом дешифрация идет только для

двух половин кодов состояния (как в прямоугольном дешифраторе).

 

 

 

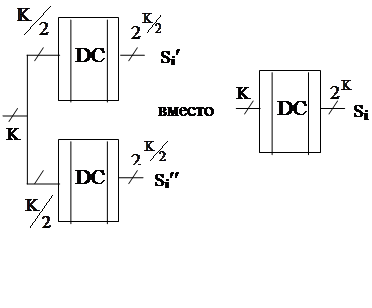
Для полного выделения состояния полу- чаются как конъюнкции сигналов с вы- ходов раздельных дешифраторов. Они реализуются в конъюнкторах КС для j
и Y, что мало влияет на их сложность.

 

Si¢

Si (Si= Si¢× Si¢¢)

S_i¢¢

 

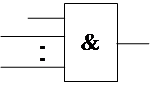(L+1) - вход

L - входов

 

Увеличение числа входов на 1 обычно мало влияет на цену.

Схемы с КС на базе

ПЛМ.

 

 

 

Сбф для КС МПА обычно состоят из большого числа бф, зависящих от боль- шого числа переменных, но эти сбф по-

чти всегда компактно представимы в ДНФ. (Число конъюнкций сбф не пре- вышает числа строк таблицы переходов МПА.)

 

 

 

Отсюда следует целесообразность ис- пользования БИС ПЛМ для КС МПА.

При такой реализации КС будет иметь входы Х ( логические условия), Р (иден- тификация частного алгоритма) и Q (сос-

тояния ЭА, представляющие состояния

МПА).

 

 

 

Использование предварительной деши- фрации состояний здесь лишено смысла.

 

Дешифрация приведет к резкому увели-

чению числа входов КС (j , Y), а число конъюнкций в сбф останется тем же, что

только ужесточит требования к ПЛМ.

 

 

 

Сбф МПА обычно не удается реализо- вать в одной БИС ПЛМ. При этом син-
тез КС выполняется в условиях нехват-

ки конъюнкторов и выходов ПЛМ.

 

 

 

При разложении КС по нескольким

ПЛМ в условиях нехватки конъюнкто-
ров следует учитывать, что как прави-

ло выходы ПЛМ объединяются конъюн-

ктивно, что требует разбиения или .

 

 

В первом случае для =j₁ Ú j₂ Ú...Ú j_q имеем

 

 

369 Отсюда следует схема

 

 

y_i могут быть получены либо по ДНФ , либо инверсией ДНФ 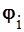на выходном инверторе ПЛМ.

 

 

Следует помнить , что реализуя , мы обрабатываем (и соответственно выпи-

сываем как исходную) .

Выражения для использоваться нами

не будут.

 

 

В втором случае для = j₁ Ú j₂ Ú...Ú j_q имеем

 

 

 

 

372 Отсюда следует схема

	y1

 

yq

. . .

Как и ранее, y_i могут быть получены либо как ДНФ , либо как инверсия ДНФ .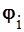

 

 

 

Использование дополнительного инвер- тора нежелательно, но иногда осущест- вляется разделение по , а не по , ес-

ли инверсия может быть получена без

затрат оборудования.

 

 

Это может быть, например, при реали- зации функций возбуждения D - триг- геров, имеющих инверсный выход .

 

 

КС на базе ПЛМ могут упрощаться

при специальном кодировании состоя-

ний МПА. Добиться этого можно так.

Сначала сбф КС рассматривается с

незакодированными состояниями.(Вмес-

то кодов состояний берутся их имена: S₀ ,

S₁, S₂, ...)

 

 

 

Очень удобно при этом рассматривать сбф , представленные обратной струк- турной таблицей переходов.

 

 

Затем всюду, где это удастся, не простые импликанты заменяются простыми.

Например, пара строк таблицы

 

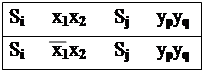заменяется на одну

	Six2Sjypyq

 

 

 

Далее отбирается k конъюнкций для очередной формируемой ПЛМ (k - чис-

ло конъюнкторов ПЛМ). Рассматри-

ваются конъюнкции, отличающиеся

только именами входящих в них сос- тояний и являющиеся импликантами одних и тех же бф.

 

 

Для них выбираются коды состоя-

ний так, чтобы они давали склеива-

ние конъюнкций и соответственно

сокращение их числа. (Разрядность

кодов определяется по числу состоя-

ний.Сами коды можно выбирать про-

извольно, но не совпадающими с ра-

нее использованными.)

 

Например, имея

 

можно взять коды для S_i, S_k, S_e и S_m так, чтобы все конъюнкции склеились.

 

 

 

Это в итоге даст строку таблицы

 

вместо четырех строк.

 

 

Если в результате выполненных дейст-

вий в ПЛМ появятся неиспользованные конъюнкторы, то к сбф ПЛМ добавля- ются новые конъюнкции, которые могут привести к фиксации новых кодов сос- тояний и т.д.

 

Кончив работать с очередной ПЛМ и зафиксировав часть кодов состояний, продолжаем такие же действия с ос- тальными ПЛМ, а в конце произволь- ным образом кодируем ранее незако-

дированные состояния.

 

 

Примечание

Исходное состояние S₀ , как правило, получает нулевой код ввиду удобства
его начальной установки.

 

 

Нехватка входов ПЛМ возникает редко,

особенно с учетом того, что МПА с очень большим числом входов строятся особым

образом ( см.3.15.3).

 

 

В заключение отметим, что в КС для

МПА Мура иногда для реализации фу-

нкций выходов Y=F(S) используются не

ПЛМ, а ПЗУ (это может быть дешевле),

так как число аргументов этих бф неве-

лико (равно числу ЭА).

 

Схемы с

Мультиплексированием

Входных сигналов.

 

 

Для МПА характерно наличие неболь- шого числа разных условий (перемен- ных), проверяемых при переходе из

любого одного его состояния. Это поз- воляет строить КС МПА с мультиплек- сированием входных сигналов, что осо- бенно выгодно при большом числе вхо- дов.

 

 

Каноническая реализация МПА имеет вид:

 

 

Мультиплексирование сокращает число входных переменных , идущих на КС j,Y

 

 

Это позволяет достаточно просто реа-

лизовать КС на БИС ПЛМ и даже ПЗУ

при числе входов МПА, превышающем

число входов БИС.

 

 

 

Схема строится так. Определяется max числа входных переменных, использу- емых в условиях перехода в одном сос- тоянии МПА. Это число L задает коли- чество новых переменных Z_{1, ...}Z_L, кото- рые будут использоваться как входные

для КС j,Y.

 

 

Для получения соответствия между входными переменными и новыми переменными Z строится таблица соответствия вида:

 

Для каждого S_i задается соответствие между входными переменными и Z.

Пример

Пусть L=5

 

 

 

Z1 Z2 Z3 Z4 Z5

395

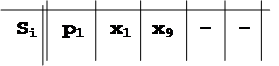Задавая соответствия, нужно делать их одинаковыми для S_i и S_j , если у них одинаковые заменяемые входные пере- менные. Кроме того желательно зано- сить переменные в те столбцы Z, в ко- торых эти переменные уже встречались. Это может упростить схему формиро- вания Z.

 

Пример

 

 

Далее строки таблицы нумеруются чис-

лами (0¸R), которые записываются дво- ичными кодами длиной r = log₂(R + 1) .

Таблица задает все варианты соответ- ствия между переменными в нумерован- ном виде, причем для каждого S_i есть номер варианта. (У одинаковых строк одинаковые номера.)

 

 

Строим схему МПА вида

 

 

 

Здесь КС R формирует по коду каждого состояния управляющий код, который задает номер варианта соответствия пе- ременных Х переменным Z. Соответ- ствие реализуется схемой из L мульти- плексоров с r управляющими входами.

 

На информационный вход D_i мульти- плексора MS_jподается переменная, ука-

занная в строке с номером i колонки Z_j.

(Если там "-", можно подавать что угод-

но.)

 

Теперь на входах КС j,Y Z₁, ... Z_L при любом состоянии МПА будут значения Х, заданные таблицей соответствия. Отсюда вытекает спо-

соб описания КС j,Y.

 

 

Сначала получается описание так, как будто КС строится без мультиплекси- рования входов, а з атем все входные переменные заменяются на Z₁, ...Z_L ,

как зафиксировано в таблице соответс-

твия.

 

 

Реализация может быть и иной при ис- пользовании специального кодирования состояний МПА.

Можно в код каждого состояния МПА внести его номер варианта соответствия

и убрать КС R.

(Подобное кодирование рассмотрено в

разделе 2.3)

 

 

 

 

 

 

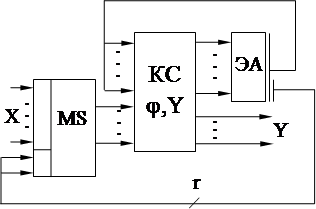Пример

 

 

(Для краткости примера не рассматриваем функцию выходов.)

 

 

Отсюда получим схему формирования Z₁ и Z₂

 

 

				R1 R2 Q1 0 0 0 0 1 0 1 0 1 1 1 0 1 0 0
			Þ

 

Теперь для Z₁ и Z₂ имеем

 

 

Закодируем S₀ ¸ S₄

			R1 R2 Q1 0 0 0 0 1 0 1 0 1 1 1 0 1 0 0
		Þ

 

410 Далее можно построить схему

 

 

Схема без мультиплексирования имела бы вид :

 

 

Итак мультиплексирование дало КС с числом входов на 2 меньше.

Если бы мы строили КС на микро- схемах ПЗУ, то нам потребовалось бы ПЗУ объемом в 4 раза меньше.

 

 

Варианты схем МПА. Кодирование состояний МПА.

 

 

 

ОА как правило представляют собой автоматы Мили по выходам оповеща- ющих сигналов. При этом УА является автоматом Мили с задержкой или авто- матом Мура.

 

 

Автоматы Мура , как правило, реализу-

ются схемой вида :

 

 

КС jобычно строится на базе ПЛМ (ПЗУ при малом числе входов), а КС Y - чаще на базе ПЗУ.

 

Перед КС j может быть схема мульти-плексирования входов, если число их ве-

лико. В этом случае КС j может стро-

иться на базе ПЗУ.

Иногда схема строится так, что функции

выходов получаются непосредственно

на выходах ЭА (полностью или частич-

но) как описано в 2.3.

 

 

 

 

Схемы с дешифрацией состояний ис- пользуются редко и строятся для не-

больших МПА на базе схем малой сте- пени интеграции. (см.3.15.1)

 

Автоматы Мили с задержкой (см. 4.2.) содержат КС j и КС Y функции кото- рых зависят от одних и тех же перемен- ных.

 

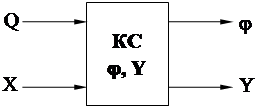Выбор способа кодирования состояний

МПА в основном зависит от способа

реализации КС в МПА.

Если КС строятся на базе ПЗУ, кодиро-

вание может быть произвольным, если
y_i ¹ Q_i .

Если КС строятся на ПЛМ, кодирование целесообразно выполнять подобно тому,

как это показано в 3.15.2.

 

 

 

Для схем с дешифрацией состояний це- лесообразно выполнять кодирование с использованием приемов, описанных в разделе 2.3.

 

Кодирование состояний, учитывающее взаимосвязь функций возбуждения и

выходов, используется редко из-за того,

что число выходов обычно заметно бо-

льше числа ЭА.

 

Выбор варианта схемы МПА связан со спецификой реализуемого автомата и осуществляется по результатам пробно-

го синтеза.