Преобразования МСА при учете ограничений на воз-можности смен логических условий

 

 

Микропрограмма (ГСА,МСА, ... ) задает

закон формирования последовательнос-

ти управляющих сигналов для микроко-

манд. Первоначально такое описание не

отражает возможных ограничений на допустимость смен входных сигналов.

 

Ограничения практически всегда есть, из-за

того, что УА работает в контуре.

 

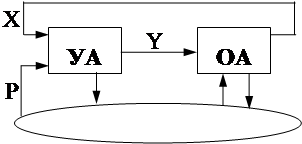P - сигналы инициирующие выполнение нужной микропрограммы.

 

Сигналы Р обычно меняются только

перед началом отработки микропрог-

раммы ( в начальном состоянии S₀ УА),

а сигналы Х зависят от предыдущих Y и

не всегда могут быть любыми.

 

 

 

Учитывая допустимость появления на входах УА различных сигналов после выполнения каждой микрокоманды, можно уточнить логические условия переходов в МСА.

 

Уточнение может привести к усложне-

нию условий переходов в МСА, но оно

позволяет строить УА, допускающие значительную минимизацию числа сос-

тояний.

 

Влияние микрокоманды K_i на оповещающие сигналы Х может быть разным. Формирующееся (новое) значение х_j мо- жет быть:

1) 1

2) 0

3) х_j (сохраняется старое)

4) _j (инвертируется старое)

5) ~ (произвольное)

 

При этом условия перехода из K_i могут уточнятся путем приписывания к ним через &:

1) x_j 2) _j

3) x¢_j 4) ¢_j

(Здесь значение ¢_j значение x_j , с кото- рым был переход в K_i , если оно не про- извольное ~ ).

 

Выполнив все возможные приписыва-

ния, и учтя влияние одних приписыва-

ний на другие, мы получим уточненную

МСА.

Процедура уточнения представляет со-

бой итерационный процесс.

 

 

 

j _i здесь постоянные условия, с кото- рыми идет переход к K_i.

 

 

x_j ( _j) приписывается к y _i, если:

n в j _i есть x_j ( _j) и K_i сохраняет

его значение;

n в j _i есть _j(x_j) и K_i инвертирует это значение;

n K_i устанавливает x_j = 1(0)

 

 

Примеры получения j _i :

 

 

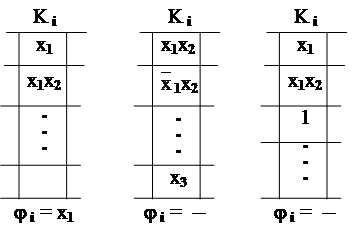Уточнение МСА обеспечивает устра нение фиктивных переходов алгоритма

 

Пример Пусть K_i дает x₁ = 0, а в МСА есть строка

K_i ® x₁K_r Ú ₁ K_q.

После уточнения получаем условие перехода в K_r x_{1 1} = 0 и строку

K_i ® ₁ K_q.

 

В заключение отметим, что рассмот-

ренная процедура уточнения МСА

имеет смысл, если в контуре «УА-ОА»

ОА - автомат Мили ( по выходам логи-

ческих условий ). Иначе микрокоманда

не будет влиять на сигналы х в следую-

щем такте.

 

 

Переход от МСА к ГСА.

 

 

 

 

См. методичку

Першеев В.Г. «Построение МПА»,

раздел 4

 

Формулы переходов Þ Скобочные формулы переходов Þ Фрагменты ГСА Þ Полная ГСА.

 

Скобочная формула - это скобочно - ортогонализированное выражение,

а не просто выражение со скобками.

 

Пример

K_i ® x₁K_p Ú _{1 2}K_qÚ ₁x₂K_r .

K_i ® x1(K_p) Ú ₁( ₂(K_q)Ú x₂ (K_r)).

 

 

 

Если МСА недоопределена (например,

после её уточнения дизъюнкция усло-

вий хотя бы одной строки не равна 1),

то получение скобочных формул пере-

хода сопровождается доопределением

условий переходов.

 

 

Доопределение выполняется так.

Сначала исходное выражение приво-

дится к скобочной форме, пока это воз-

можно, а затем переменные, не исполь-

зованные для вынесения за скобки, вы-черкиваются.

 

 

Пример

K_i ® x₁x₂x₃K_j Ú ₁x₂x₃K_pÚ _{1 2}K_q .

K_i ® x₁(x₂x₃K_j)Ú ₁(x₂x₃K_pÚ ₂K_q).

K_i ® x₁(x₂x₃K_j)Ú ₁(x₂(x₃K_p)Ú ₂(K_q)).

K_i ® x₁(K_j)Ú ₁(x₂(K_p)Ú ₂(K_q)).

 

 

 

Недоопределенные МСА порождают ГСА с висящими вершинами (без вы- ходящих связей).

 

 

Объединение ГСА.

 

 

 

 

См. методичку «Построение МПА», раздел 6,7.

 

		. . .

 

 

 

 

Построение ОГСА ( и ОМСА ) обычно сопровождается описанием способа и- нициирования работы УА: отдельным разрешающим сигналом, либо комбина- цией сигналов p₀p₁... p_m . При этом как

бы вводится пустой частный алгоритм.

 

 

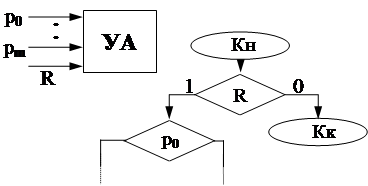
Пример введения отдельного разрешающего сигнала.