Приведение матричной игры к задаче линейного программирования

Каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и, наоборот, каждая задача линейного программирования может быть представлена, как игра. Рассмотрим способ нахождения решения игры методом линейного программирования, который особенно эффективен для игр, описываемых матрицей большой размерности.

Пусть игра задана платежной мат­рицей

		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

 

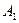
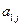
Игрок обладает стра­тегиями 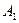, ..., , игрок — стратегиями ..., . Необ­ходимо определить оптимальные стратегии ,

где — относительные частоты применения соот­ветствующих чистых стратегий соответственно:

, .

Замечание: если в платежной матрице присутствуют нулевые или отрицательные значения «выигрышей» игрока , то к каждому элементу платежной матрицы необходимо прибавить одно и тоже положительное число , чтобы все элементы платежной матрицы стали положительными. Эта операция не изменит искомых оптимальных стратегий.

Предположим, что в данной задаче все элементы положительны: .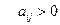

Оптимальная стратегия 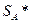удовлетворяет следующему требо­ванию: она обеспечивает игроку средний выигрыш, не мень­ший, чем цена игры 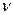, при любой стратегии игрока и выиг­рыш, равный цене игры 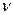, при оптимальной стратегии игрока . Так как, согласно нашему предположению, все 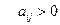, то цена игры 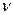> 0. Если игрок применит смешанную стратегию 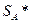против любой чистой стратегии игрока , то он получит средний выигрыш, или математическое ожидание выигрыша ( ).

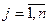Для оптимальной стратегии 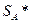все средние выигрыши не меньше цены игры 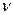, поэтому можно составить систему неравенств:

(6.2)

Каждое из неравенств разделим на число 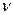> 0. Введем новые переменные:

Получим

(6.3)

Цель игрока — максимизировать свой гарантированный вы­игрыш, т.е. цену игры .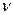

Разделим на равенство , получим, что переменные 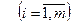удовлетворяют условию: 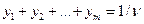. Максимизация цены игры 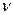эквивалентна мини­мизации величины 1/ 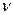, поэтому задача может быть сформулиро­вана следующим образом: определить значения переменных 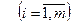, минимизирующие линейную функцию и удовлетворяющие линейным ограничени­ям (6.3).

Это задача линейного программирования, решая которую, получим оптимальное решение и оптимальную стратегию .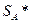

Для определения оптимальной стратегии следует учесть, что игрок стремится минимизировать гаранти­рованный выигрыш 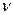, т.е. в этом случае находится max(1/ 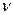). При этом переменные должны будут удовлетворять неравенствам

(6.4)

которые следуют из того, что средний проигрыш игрока не будет пре­восходить цены игры 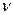, какую бы чистую стратегию не применял игрок А.

Если обозначить 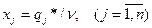, то получим систему неравенств:

(6.5)

переменные, которой удовлетворяют условию .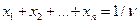

Задачу можно сформулировать следующим образом: определить значения переменных 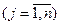, удовлетворяющие системе неравенств (6.5) и максимизирующие линейную функцию .

Решение сформулированной задачи определяет оптимальную стратегию .

Нетрудно заметить, что сформулированные выше две задачи являются взаимно-двойственными задачами линейного программирования.

Решив, сформулированные задачи ЛП, вычислим

, , .

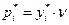Задача №6.6.

Найти решение игры, заданной платежной матрицей:

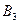
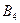
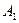
				-5	-5
	-2		-1		-2
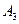
	-3		-3		-3
					2 -2

 

Решение.

Игра не имеет седловой точки: , . Так как , то решение должно лежать в области смешанных стратегий.

Нижняя цена игры – число отрицательное ( ), поэтому возможно, значение цены игры 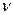не будет положительным. Число , которое необходимо прибавить ко всем элементам матрицы должно быть не меньше 2. Пусть , в этом случае все элементы матрицы становятся положительными. Платежная матрица примет вид:

 

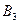
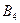
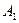
Задача ЛП для игрока формулируется следующим образом: найти минимальное значение функции (6.6) при условии выполнения ограничений(6.7):

(6.6)

(6.7)

Для игрока - найти максимальное значение функции (6.8)

при условии выполнения ограничений (6.9):

(6.8)

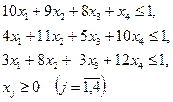(6.9)

Получили пару задач линейного программирования.

Решив задачи с помощью надстройки «Поиск решения», получим оптимальные решения : ; .

При этом .

Вычислим цену игры и вероятности для оптимальных смешанных стратегий игроков и :

;

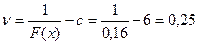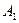Следовательно, если игрок будет применять стратегии и с частотой и , то он гарантирует себе выигрыш не меньше, чем цена игры , как бы не вел себя противник. При этом, если игрок в трех случаях из четырех будет применять стратегию 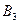, в остальных случаях стратегию 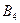, то он гарантирует себе проигрыш не более, чем цена игры . Если же игрок , воспользуется своей оптимальной стратегией, а игрок воспользуется хотя бы раз одной из своих пассивных стратегий или , то выигрыш игрока может оказаться и больше цены игры. Аналогично, если же игрок , воспользуется своей оптимальной стратегией, а игрок воспользуется хотя бы раз своей пассивной стратегией 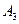, то проигрыш игрока может оказаться меньше, чем цена игры.

Моделирование экономических ситуаций в терминах "игры с природой"

Выше рассматривались игровые модели, в которых в качестве оппонента выступал противник, принимающий решения и выбирающий стратегии по определенным правилам. В экономической практике нередко приходится принимать решения (выбирать стратегии), не имея информации о возможном сопернике в условиях неопределенности и риска. Для описания таких ситуаций разработан математический аппарат игр с "природой". "Природа" в теории игр - объективная действительность, некая незаинтересованная сторона, "поведение" которой неизвестно, но, во всяком случае, не содержит элемента сознательного противодействия нашим планам.

Формально изучение игр с "природой", также как и стратегических, должно начинаться с построения платежной матрицы.

Рассмотрим пример «игры с природой».

 

Задача №6.7

Предприятие может выпускать три вида продукции , получая при этом прибыль, зависящую от спроса, который может быть в одном из трех состояний . Дана матрица

,

ее элементы 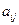характеризуют прибыль, которую получит предприятие при выпуске -й продукции с 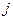-м состоянием спроса.

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.

Решение.

Задача сводится к игровой модели, в которой игра предприятия против спроса задана платежной матрицей. Проверим игру на наличие седловой точки:

.

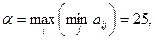
Решение игры надо искать в смешанных стратегиях. Цена игры лежит между нижней и верхней ценами: .

Нас интересует стратегия игрока . Задача ЛП для игрока формулируется следующим образом: найти минимальное значение функции (6.5) при условии выполнения ограничений(6.6):

(6.5)

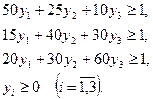(6.6)

Решив задачу с помощью надстройки «Поиск решения», получим оптимальный план 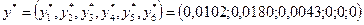. При этом . Вычислим цену игры и вероятности для оптимальных смешанных стратегий предприятия :

Данное решение показывает, что предприятие должно выпускать 31,4% продукции 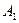; 55,4% продукции и 13,2% - ; при этом гарантированная величина средней прибыли равна 30,77 д.е.

 

Пример №6.8.

Сельскохозяйственное предприятие имеет возможность выращивать две культуры — 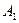и .

В результате многолетних наблюдений составлена матрица дохода от реализации урожаев сельскохозяйственного предприятия (в млн. руб.) в зависимости от состояний погоды: засушливое лето ( ), нормальное лето ( ), влажное лето ( 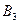). Матрица дохода в зависимости от состояния погоды имеет вид: .

Необходимо определить, как сеять культуры, если при прочих равных условиях урожаи зависят от погоды, а план посева должен обеспечить наибольший доход (доход от реализации выращенной культуры определяется полученным объемом).

Решение.

В зоне рискованного земледелия (а таковой является большая часть России) планирование посева должно осуществляться с учетом наименее благоприятного состояния погоды.

Таким образом, одной из сторон выступает сельскохозяйственное предприятие (игрок ), заинтересованное в том, чтобы получить наибольший доход, а другой стороной - «природа» (игрок ), способная навредить сельскохозяйственному предприятию в максимальной степени (от нее зависят погодные условия), хотя и не преследующая прямо противоположные цели.

Принятие природы за противника равносильно планированию посева с учетом наиболее неблагоприятных условий; если же погодные условия окажутся благоприятными, то выбранный план дает возможность увеличить доход.

Налицо антагонистический конфликт, в котором у игрока две стратегии, а у игрока три.

Нетрудно заметить, что седловой точки у этой матрицы нет. Поэтому оптимальная стратегия игрока будет смешанной. Построим модель задачи ЛП

Решив задачу с помощью надстройки «Поиск решения», получим оптимальный план ; . Вычислим цену игры и вероятности для оптимальных смешанных стратегий сельскохозяйственного предприятия:

Полученное решение сельскохозяйственное предприятие может использовать так:

на 3/5 всех площадей выращивать культуру А₁;

на 2/5 всех площадей выращивать культуру А₂.

и получать прибыль в размере, не меньшем 4,2 млн. руб.