 |
Главная |
Нижняя и верхняя цена игры
|
из
5.00
|
Определим стратегию игрока  , которая обеспечила бы ему наибольший из возможных выигрышей вне зависимости от того как поведет себя игрок В. Выбирая стратегию, мы должны руководствоваться тем, что наш противник действует разумно и на любую нашу стратегию отвечает той стратегией из числа имеющихся у него, которая обеспечивает нам минимальный выигрыш.
, которая обеспечила бы ему наибольший из возможных выигрышей вне зависимости от того как поведет себя игрок В. Выбирая стратегию, мы должны руководствоваться тем, что наш противник действует разумно и на любую нашу стратегию отвечает той стратегией из числа имеющихся у него, которая обеспечивает нам минимальный выигрыш.
То есть, если мы воспользуемся стратегией  , то при разумных действиях противника наш выигрыш будет равен
, то при разумных действиях противника наш выигрыш будет равен  . Обозначим, через
. Обозначим, через  наибольшее значение из всех
наибольшее значение из всех  :
:  . Величина
. Величина  называется нижней ценой игрыили максиминным выигрышем (максимином). Число
называется нижней ценой игрыили максиминным выигрышем (максимином). Число  лежит в определенной строке матрицы; та стратегия игрока
лежит в определенной строке матрицы; та стратегия игрока  , которая соответствует этой строке, называется максиминной стратегией. Очевидно, если игрок
, которая соответствует этой строке, называется максиминной стратегией. Очевидно, если игрок  будет придерживаться максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш, во всяком случае, не меньший
будет придерживаться максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш, во всяком случае, не меньший  .
.
Нижняя цена игры  – гарантированный выигрыш игрока
– гарантированный выигрыш игрока  при любой стратегии противника (это тот минимум, который игрок
при любой стратегии противника (это тот минимум, который игрок  может себе обеспечить, действуя наиболее осторожно).
может себе обеспечить, действуя наиболее осторожно).
Очевидно, аналогичные рассуждения можно провести и за противника  . Выдвигая стратегию
. Выдвигая стратегию  , противник понимает, что мы ответим на эту стратегию той стратегией из всех возможных, которая даст нам максимальный выигрыш равный
, противник понимает, что мы ответим на эту стратегию той стратегией из всех возможных, которая даст нам максимальный выигрыш равный  . Обозначим через
. Обозначим через  наименьшее значение из всех
наименьшее значение из всех  :
:  . Величина
. Величина  называется верхней ценой игры (минимаксом). Соответствующая минимаксному выигрышу стратегия противника называется его минимаксной стратегией. Придерживаясь своей наиболее осторожной минимаксной стратегии, игрок
называется верхней ценой игры (минимаксом). Соответствующая минимаксному выигрышу стратегия противника называется его минимаксной стратегией. Придерживаясь своей наиболее осторожной минимаксной стратегии, игрок  может гарантировать себе проигрыш не более
может гарантировать себе проигрыш не более  , вне зависимости от того, как поступит игрок
, вне зависимости от того, как поступит игрок  .
.
Верхняя цена игры - гарантированный проигрыш игрока  при любой стратегии противника (это тот минимальный проигрыш, который может себе обеспечить игрок
при любой стратегии противника (это тот минимальный проигрыш, который может себе обеспечить игрок  , действуя наиболее осторожно).
, действуя наиболее осторожно).
Принцип осторожности, диктующий игрокам выбор соответствующих стратегий в теории игр в ее приложениях, часто называют принципом минимакса.
Задача № 6.1.
Игроки  и
и  одновременно и независимо друг от друга пишут одно из трех чисел: 1, 2 или 3. Если сумма написанных чисел четная, то
одновременно и независимо друг от друга пишут одно из трех чисел: 1, 2 или 3. Если сумма написанных чисел четная, то  платит
платит  эту сумму в рублях; если она нечетная, то, наоборот,
эту сумму в рублях; если она нечетная, то, наоборот,  платит
платит  эту сумму. Требуется проанализировать игру; составить ее матрицу; найти нижнюю и верхнюю цены игры.
эту сумму. Требуется проанализировать игру; составить ее матрицу; найти нижнюю и верхнюю цены игры.
Решение.
Игра состоит из двух ходов (ход игрока  и ход игрока
и ход игрока  ), оба хода личные. У игрока
), оба хода личные. У игрока  три стратегии:
три стратегии: 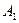 - написать число 1;
- написать число 1;  – написать число 2;
– написать число 2; 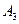 – написать число 3. У противника (игрока
– написать число 3. У противника (игрока  ) тоже три стратегии. Игра представляет собой игру 3
) тоже три стратегии. Игра представляет собой игру 3  3 с матрицей, приведенной ниже.
3 с матрицей, приведенной ниже.


| 
| 
| 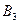
| 
|
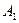
| 2 | -3 | 4 | -3 |

| -3 | 4 | -5 | -5 |
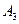
| 4 | -5 | 6 | -5 |

| 4 | 4 | 6 | 4 -3 |
Нижняя цена игры  ; верхняя цена игры
; верхняя цена игры 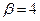 . Максиминная стратегия игрока
. Максиминная стратегия игрока  это стратегия
это стратегия 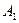 ; применяя ее систематически, игрок
; применяя ее систематически, игрок  может твердо рассчитывать на выигрыш не менее, чем «-3», т.е. его проигрыш не составит более, чем 3 рубля в каждой игре. Аналогично, применяя стратегии
может твердо рассчитывать на выигрыш не менее, чем «-3», т.е. его проигрыш не составит более, чем 3 рубля в каждой игре. Аналогично, применяя стратегии  ,
,  игрок
игрок  обеспечит себе этим проигрыш не более, чем в четыре рубля. Если же игрок
обеспечит себе этим проигрыш не более, чем в четыре рубля. Если же игрок  отступит от своей минимаксной стратегии (например, выберет стратегию
отступит от своей минимаксной стратегии (например, выберет стратегию  ) противник может, выбрав стратегию
) противник может, выбрав стратегию 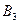 , свести выигрыш игрока
, свести выигрыш игрока  к «-5». Отступление же игрока
к «-5». Отступление же игрока  от своей минимаксной стратегии может свести его проигрыш к 6 рублям.
от своей минимаксной стратегии может свести его проигрыш к 6 рублям.
Задача №6.2.
В распоряжении игрока  имеются три вида вооружения:
имеются три вида вооружения: 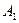 ,
,  ,
, 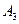 . У противника
. У противника  имеется три вида самолетов
имеется три вида самолетов  ,
,  ,
, 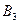 . Задача игрока
. Задача игрока  поразить самолет; задача противника (игрока
поразить самолет; задача противника (игрока  ) – сохранить его. При применении вооружения
) – сохранить его. При применении вооружения 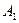 самолеты
самолеты  ,
,  ,
, 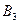 поражаются соответственно с вероятностями: 0,9; 0,4; 0,2. При применении вооружения
поражаются соответственно с вероятностями: 0,9; 0,4; 0,2. При применении вооружения  самолеты поражаются с вероятностями: 0,3; 0,6; 0,8, а при применении вооружения
самолеты поражаются с вероятностями: 0,3; 0,6; 0,8, а при применении вооружения 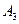 – 0,5; 0,7; 0,2. Сформулировать ситуацию в терминах теории игры. Определить верхнюю и нижнюю цены игры.
– 0,5; 0,7; 0,2. Сформулировать ситуацию в терминах теории игры. Определить верхнюю и нижнюю цены игры.
Решение.
Ситуация может рассматриваться как игра 3  3 с двумя личными ходами и одним случайным. Личный ход игрока
3 с двумя личными ходами и одним случайным. Личный ход игрока  – выбор типа вооружения. Личный ход игрока
– выбор типа вооружения. Личный ход игрока  – выбор вида самолета. Случайный ход - действие вооружения; этот ход может окончиться поражением или не поражением самолета. Выигрыш игрока
– выбор вида самолета. Случайный ход - действие вооружения; этот ход может окончиться поражением или не поражением самолета. Выигрыш игрока  равен единице, если самолет поражен, и равен нулю в противном случае. Стратегиями игрока
равен единице, если самолет поражен, и равен нулю в противном случае. Стратегиями игрока  являются три варианта вооружения; стратегиями игрока
являются три варианта вооружения; стратегиями игрока  являются три варианта самолетов. Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения данного самолета данным оружием. Ниже приводится матрица игры:
являются три варианта самолетов. Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения данного самолета данным оружием. Ниже приводится матрица игры:
 
| 
| 
| 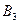
| 
|
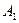
| 0,9 | 0,4 | 0,2 | 0,2 |

| 0,3 | 0,6 | 0,8 | 0,3 |
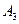
| 0,5 | 0,7 | 0,2 | 0,2 |

| 0,9 | 0,7 | 0,8 | 0,7 0,3 |
Нижняя цена игры  =0,3; верхняя цена игры
=0,3; верхняя цена игры  =0,7. Наиболее осторожная (максиминная) стратегия игрока
=0,7. Наиболее осторожная (максиминная) стратегия игрока  – это стратегия
– это стратегия  ; пользуясь вооружением
; пользуясь вооружением  , игрок
, игрок  гарантирует себе, что будет поражать самолеты в среднем не менее, чем с частотой 0,3. Наиболее осторожной (минимаксной) стратегией игрока
гарантирует себе, что будет поражать самолеты в среднем не менее, чем с частотой 0,3. Наиболее осторожной (минимаксной) стратегией игрока  будет стратегия
будет стратегия  . Выбирая второй вид самолетов, игрок
. Выбирая второй вид самолетов, игрок  может быть уверен, что он будет поражаться не более чем с частотой 0,7.
может быть уверен, что он будет поражаться не более чем с частотой 0,7.
Продемонстрируем на данном примере свойство неустойчивости минимаксных стратегий.До тех пор пока оба игрока придерживаются своих наиболее осторожных стратегий, средний выигрыш игрока  равен 0,6. Это число больше, чем нижняя цена игры
равен 0,6. Это число больше, чем нижняя цена игры  =0,3, но меньше, чем верхняя цена игры
=0,3, но меньше, чем верхняя цена игры  =0,7. Теперь допустим, что игроку
=0,7. Теперь допустим, что игроку  стало известно, что игрок
стало известно, что игрок  применяет стратегию
применяет стратегию  , он немедленно применит стратегию
, он немедленно применит стратегию  , чем сведет выигрыш игрока
, чем сведет выигрыш игрока  к 0,3. В свою очередь, на стратегию
к 0,3. В свою очередь, на стратегию  игрок
игрок  может ответить стратегией
может ответить стратегией 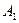 , дающей выигрыш 0,9 и т.д.
, дающей выигрыш 0,9 и т.д.
Таким образом, положение, при котором оба игрока пользуются своими минимаксными стратегиями, является неустойчивым и может быть нарушено поступившими сведениями о стратегии противоположной стороны.
Однако существуют некоторые игры, для которых минимаксные стратегии являются устойчивыми. Это те игры, для которых нижняя цена игры равна верхней:  .
.
Если нижняя цена игры равна верхней, то их общее значение называется чистой ценой игры или просто ценой игры.
Задача №6.3
Пусть игра задана платежной матрицей 4  4:
4:


| 
| 
| 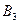
| 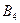
| 
|

| 0,4 | 0,5 | 0,9 | 0.3 | 0,3 |

| 0,8 | 0,4 | 0,3 | 0.7 | 0,3 |

| 0,7 | 0,6 | 0,8 | 0.9 | 0,6 |

| 0.7 | 0.2 | 0.4 | 0.6 | 0.2 |

| 0,8 | 0,6 | 0,8 | 0.9 | 0.6 0.6 |
Найдем нижнюю цену игры:  =0,6. Найдем верхнюю цену игры:
=0,6. Найдем верхнюю цену игры:  =0,6. Они оказались равными. Следовательно, у игры есть чистая цена
=0,6. Они оказались равными. Следовательно, у игры есть чистая цена 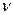 , равная
, равная  .
.
Элемент 0,6, выделенный в платежной матрице, является одновременно минимальным в своей строке и максимальным в своем столбце. В геометрии точку на поверхности, обладающую аналогичным свойством, называют седловой точкой; по аналогии этот термин применяется и в теории игр. Элемент матрицы, обладающий этим свойством, называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
Седловая точка – платеж, который одновременно является наибольшим в своем столбце и наименьшим в своей строке.
Стратегии, соответствующие седловой точке, называют оптимальными стратегиями (в данном примере  ,
, 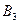 ), а их совокупность называют решением игры.
), а их совокупность называют решением игры.
Решение игры обладает замечательным свойством. Если один из игроков придерживается своей оптимальной стратегии, а другой игрок будет любым способом отклоняться от своей оптимальной стратегии, то для игрока допустившего отклонение, это никогда не может оказаться выгодным: в лучшем случае выигрыш его останется неизменным, в худшем случае его выигрыш уменьшится (проигрыш увеличится).
Это утверждение легко проверить на примере рассматриваемой игры с седловой точкой. Мы видим, что в случае игры с седловой точкой минимаксные стратегии обладают своеобразной «устойчивостью»: если одна сторона придерживается своей минимаксной стратегии, то для другой невыгодно отклоняться от своей минимаксной стратегии. В данном случае, даже если у игроков имеются сведения о том, что противник избрал свою оптимальную стратегию, это не изменит поведения игроков. Пара оптимальных стратегий в игре с седловой точкой является как бы «положением равновесия»: любое отклонение от оптимальной стратегии приводит отклоняющегося игрока к невыгодным последствиям, вынуждающим его вернуться в исходное положение.
|
из
5.00
|
Обсуждение в статье: Нижняя и верхняя цена игры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

