 |
Главная |
КОНТРОЛЬНАЯ РАБОТА № 1. Вычислить пределы:
|
из
5.00
|
Задание 1
Вычислить пределы:
1. 
2. 
3. 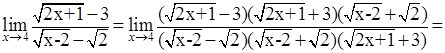


4. 

5. 
Делаем замену  ,
, 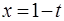 ,
, 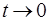 .
.


6. 
 .
.
Вычислить пределы.
1. 

2. 
3. 


4. 

Задание 2
При решении примеров используются формулы производных сложных функций  , где
, где 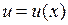 :
:
 и другие.
и другие.
1. 
 .
.
2.  Преобразуем:
Преобразуем: 

 .
.
 .
.
3. 


4. 


 .
.
5. 
 логарифмируем:
логарифмируем: 
 дифференцируем:
дифференцируем:


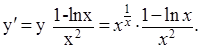
6. 
 логарифмируем:
логарифмируем: 
 дифференцируем:
дифференцируем:



7. 
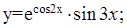
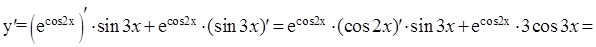

 .
.
Задание 3
Провести полное исследование функций и построить графики.
а)  ; б)
; б)  .
.
Решение:
а)  .
.
1) Функция определена на всей оси Ох, кроме точки  , где она терпит бесконечный разрыв.
, где она терпит бесконечный разрыв.
2) Находим наклонные асимптоты  :
:
 ;
;

Наклонная асимптота  . Вертикальная асимптота
. Вертикальная асимптота  .
.
Находим критические точки, в которых первая или вторая производная равна нулю, либо не существует:
 ;
;
 .
.
Критическими точками будут  и
и 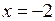 , где
, где  =0 . В точке
=0 . В точке  функция не существует.
функция не существует.
Из формулы для  следует, что y<0 при
следует, что y<0 при  , и y>0 при
, и y>0 при  .
.
Из формулы для  следует, что при x из (-
следует, что при x из (- 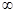 ,-2)
,-2)  >0, т.е. функция возрастает; в интервале (-2,-1)
>0, т.е. функция возрастает; в интервале (-2,-1)  <0 – функция убывает, а точка
<0 – функция убывает, а точка 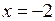 является точкой максимума. В интервале (0,+
является точкой максимума. В интервале (0,+ 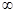 )
)  >0 – функция возрастает. В интервале (-1;0) производная
>0 – функция возрастает. В интервале (-1;0) производная  <0 и функция убывает. Точка
<0 и функция убывает. Точка  – точка минимума.
– точка минимума.
В интервале (- 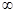 ;-1)
;-1)  <0 – график функции выпуклый, в интервале (-1; +
<0 – график функции выпуклый, в интервале (-1; + 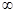 )
)  >0 - график вогнутый.
>0 - график вогнутый.
Результаты исследований сведем в таблицу:
| x | (- 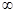 ,-2) ,-2)
| -2 | (-2,-1) | -1 | (-1,0) | (0,+ 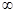 ) )
| |
| y | - | -4 | - | - 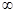
| + | + | |
 
| + | - | не сущ. | - | + | ||

| - | - | - | не сущ. | + | + | + |
| Выводы: | Функция возрастает; график выпукл. | Точка максимума | Функция убывает; график выпукл. | Точка разрыва | Функция убывает; график вогнут. | Точка минимума | Функция возрастает; график вогнут. |
Строим график:

б)  .
.
1) Функция определена, если  >0 , т.е.
>0 , т.е. 
В точках 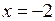 и
и  функция имеет бесконечный разрыв, так как:
функция имеет бесконечный разрыв, так как:
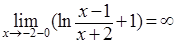 ;
;  .
.
2) Прямые 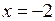 и
и  – вертикальные асимптоты, т.к. lim |y|=
– вертикальные асимптоты, т.к. lim |y|=  в этих точках.
в этих точках.
Наклонные асимптоты:
 ;
;  ;
;
Таким образом, уравнение асимптоты  .
.
3) Находим  и
и  :
:  ;
;
 .
.
Критические точки: 
 0, в точках
0, в точках 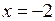 и
и  функция не существует;
функция не существует;
 =0 , точка
=0 , точка  – критическая точка;
– критическая точка;  ОДЗ.
ОДЗ.
 >0 в интервалах (-
>0 в интервалах (- 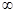 ;-2) и (1;+
;-2) и (1;+ 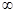 ) – функция возрастает;
) – функция возрастает;
 <0 в интервале (1;+
<0 в интервале (1;+ 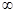 ) – график функции выпуклый;
) – график функции выпуклый;
 >0 в интервале (-
>0 в интервале (- 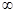 ;-2) – график функции вогнутый;
;-2) – график функции вогнутый;
Из условия у=0 найдем точку пересечения кривой с осью Ох.

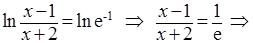



 .
.
Составим таблицу, включающую точки 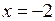 и
и  ;
;  .
.
| x |
(-  ,-2) ,-2)
| -2 | (1,  ). ).
|  . .
| (  ,+ ,+  ) )
| |
| y | + | + 
| - 
| - | + | |
 
| + | не сущ. | не сущ. | + | + | + |

| + | не сущ. | не сущ. | - | - | - |
| Выводы: | Функция возрастает; график вогнут. | Вертикальная асимптота. | Вертикальная асимптота. | Функция возрастает; график выпукл. | Функция возрастает; график выпукл. |
Строим график функции:

Образец выполнения контрольной работы № 2
Задание 4
Найти неопределённые интегралы. В пунктах а) и б) результаты проверить дифференцированием.
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Решение.
а) 

 .
.
Проверка.
Найдём производную от полученного результата:

 .
.
Получили исходную подынтегральную функцию. Значит, интеграл найден верно.
Ответ:  .
.
б)  находят интегрированием по частям. Формула интегрирования по частям имеет вид
находят интегрированием по частям. Формула интегрирования по частям имеет вид
 .
.
Примем  . Первое равенство дифференцируем, второе интегрируем:
. Первое равенство дифференцируем, второе интегрируем:
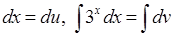 .
.
Получаем: 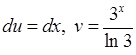 . Применяя формулу интегрирования по частям, находим:
. Применяя формулу интегрирования по частям, находим:
 .
.
Проверка.
 .
.
Интеграл вычислен верно.
Ответ:  .
.
в)  – интеграл от рациональной дроби. Найдём корни многочлена, стоящего в знаменателе, т. е. решим уравнение
– интеграл от рациональной дроби. Найдём корни многочлена, стоящего в знаменателе, т. е. решим уравнение  :
:
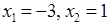
и разложим знаменатель дроби на множители, а дробь – на сумму двух простейших дробей:
 .
.
Приравняем числители первой и последней дроби:
 .
.
Это тождество должно выполняться при всех  .
.
Подставим  :
:  .
.
Теперь подставим  :
:  .
.
Значит, разложение дроби имеет вид:
 .
.
Найдём теперь заданный интеграл:

 .
.
Ответ:  .
.
г) В интеграле  сделаем замену переменной
сделаем замену переменной  , откуда
, откуда  . Дифференцируя обе части, найдём:
. Дифференцируя обе части, найдём:
 .
.
После замены интеграл принимает вид:

= 
 .
.
Ответ:  .
.
Задание 5
Вычислить несобственный интеграл или доказать его расходимость:
 .
.
Решение.
Функция  не ограничена в окрестности точки x = 3. Поэтому точка x = 3 – особая. По определению несобственного интеграла
не ограничена в окрестности точки x = 3. Поэтому точка x = 3 – особая. По определению несобственного интеграла
 Ответ:
Ответ:  .
.
Задание 6
Вычислить площадь фигуры, ограниченной линиями
 .
.
Решение.
Искомая площадь заштрихована на рисунке.

Её величина вычисляется по формуле

 .
.
Ответ:  .
.
КОНТРОЛЬНАЯ РАБОТА № 3
Задание 7
Дано:
A=  , B=
, B=  , C=
, C=  .
.
Найти: 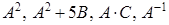 .
.
Решение:
 =
=  =
=  =
=
=  ;
;
 =
=  +5
+5  =
=  +
+  =
=  ;
;
 =
= 
 =
=  =
=  ;
;
 , где
, где  ;
;
 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  .
.

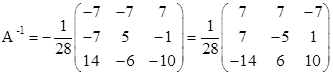
Проверка:

 =
=
 =
=
 .
.
Получили, что  , значит обратная матрица
, значит обратная матрица  вычислена верно.
вычислена верно.
Задание 8
Доказать совместность системы уравнений

и решить её а) методом Гаусса, б) матричным методом.
Решение:
Матрица системы  ,
,
расширенная матрица  .
.
Вычислим ранги матрицы А и матрицы С.
Применим к матрицам А и C элементарные преобразования. Обозначим схематически умножение i-й строки на число m и прибавление полученной строки к k-й строке.

 Аналогичное обозначение применим к столбцам.
Аналогичное обозначение применим к столбцам.
 Деление строки (столбца) на число N обозначим
Деление строки (столбца) на число N обозначим
 |
A= 














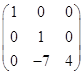





 .
.
Следовательно, ранг А = 3.

 Вычислим ранг матрицы С.
Вычислим ранг матрицы С.
 C =
C = 

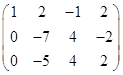



 |

















 .
. 
Следовательно, ранг С = 3
Так как ранг А = ранг С, то система совместна.
а) Решение системы методом Гаусса.
 Рассмотрим расширенную матрицу С и осуществим преобразование со строками
Рассмотрим расширенную матрицу С и осуществим преобразование со строками
 C=
C= 
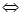
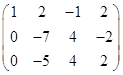






 .
.
Коэффициенты матрицы G являются коэффициентами системы уравнений:
 Получим:
Получим: 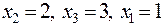 .
.
б) Решение системы матричным методом.
Систему уравнений

можно представить в матричном виде, если обозначить матрицы:
A=  ; B=
; B=  ; X=
; X= 
Система уравнений в матричном виде: A 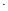 X=B
X=B
Решение имеет вид:  X=
X= 
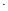 B
B
Найдем 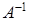



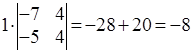 .
.


Вычислим алгебраические дополнения:











 X=
X= 
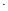 B =
B = 
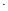
 =
=  =
=  =
= 
Следовательно,  .
.
Задание 9
Даны координаты вершин пирамиды  :
:
 (1;3;0) ;
(1;3;0) ;  (7;4;1) ;
(7;4;1) ;  (2;9;6) ;
(2;9;6) ;  (4;6;6).
(4;6;6).
Найти:
1) длину ребра  ;
;
2) угол между ребрами  и
и  ;
;
3) уравнение прямой  ;
;
4) уравнение плоскости  ;
;
5) угол между ребром  и гранью
и гранью  ;
;
6) объём пирамиды;
7) уравнение высоты, опущенной из вершины  на грань
на грань  ;
;
8) сделать чертеж.
Решение:
1) координаты векторов: 
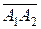 =(6;1;1) ;
=(6;1;1) ;  =(1,6,6);
=(1,6,6);  =(3;3;6).
=(3;3;6).
Длины векторов:  =
=  =
=  ;
;  =
=  =
=  .
.
2) Угол между ребрами  и
и  :
:


 ,
,

 .
.
3) уравнение прямой  :
: 
4) уравнение плоскости  :
: 
(x-1)(6-6) - (y-3)(6 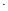 6-1
6-1 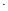 1)+z(6
1)+z(6 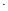 6-1
6-1 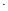 1)=0
1)=0  -35(y-3) + 35z = 0
-35(y-3) + 35z = 0  y-z-3=0
y-z-3=0
5) угол  между ребром
между ребром  и гранью
и гранью  (плоскостью
(плоскостью  )
)

 ,
,
 .
.
6) объем пирамиды:

| (Из 3-го столбца вычтем 2-й столбец) |  . .
|
7) уравнение высоты, опущенной из вершины  на грань
на грань  . Направляющий вектор высоты – это нормальный вектор плоскости
. Направляющий вектор высоты – это нормальный вектор плоскости  на грань
на грань  . Каноническое уравнение высоты:
. Каноническое уравнение высоты:  .
.
8) Чертеж:

СОДЕРЖАНИЕ
| Введение ….………………………….………………………. | |
| Учебный план дисциплины ……...…….…………………… | |
| Цели и задачи дисциплины ………………….……………… | |
| Общие рекомендации студенту заочного отделения по изучению курса математики ..........………...…………..…… | |
| Указания по выполнению контрольных работ .…………… | |
| Таблица вариантов .………………………..………………… | |
| Рекомендуемая литература ………………….……………… | |
| Рабочая учебная программа курса и методические указания к изучению предмета …………………………………… | |
| ЗАДАНИЯ КОНТРОЛЬНЫХ РАБОТ ……………………… | |
| Контрольная работа № 1 ………………………………… | |
| Контрольная работа № 2 ……….………………………… | |
| Контрольная работа № 3 …………………….…………… | |
| ОБРАЗЦЫ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ .….. | |
| Контрольная работа № 1 …….…………………………… | |
| Контрольная работа № 2 ………………………………… | |
| Контрольная работа № 3 ………………………………… |
|
из
5.00
|
Обсуждение в статье: КОНТРОЛЬНАЯ РАБОТА № 1. Вычислить пределы: |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

