Исследование функции с помощью производной

Государственное автономное профессиональное образовательное учреждение Свердловской области

«Сергинский многопрофильный техникум»

 

 

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

Методические указания и индивидуальные задания к контрольной работе

 

для студентов заочного отделения

специальность: 230401 Информационные системы (по отраслям)

 

Верхние Серги

 

Часть 2

Основы математического анализа.

Методы дифференциального и интегрального исчисления.

Дифференциальные уравнения.

Методические указания и индивидуальные задания

 

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
И РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ

 

Основы математического анализа

 

Понятие функции

Функция

Пусть даны два множества X и Y. Если каждому элементу поставлен в соответствие единственный элемент 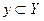, то говорят, что на множестве X задана однозначная функция .

Графиком функции называется множество точек .

Функция называется четной на множестве D, если выполняется равенство , . График четной функции симметричен относительно оси .

Функция называется нечетной на множестве D, если выполняется равенство , . График нечетной функции симметричен относительно начала координат.

Функция называется возрастающей (убывающей) на множестве D, если для любых , , выполняется неравенство ( ).

Функция называется ограниченной на множестве D, если такое число , что выполняется .

Функция называется периодической на множестве D, если такое число 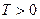, что выполняется . Наименьшее из этих чисел Т принято называть периодом функции .

Пусть задана функция с областью определения D и множеством значений Е. если каждому значению соответствует единственное значение , то определена функция с областью определения E и множеством значений D. Такая функция называется обратной к функции и записывается . Функции и называются взаимообратными.

Любая строго монотонная функция имеет обратную.

Пусть функция 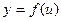определена на множестве D, а функция на множестве D_1, причем соответствующее значение . Тогда на множестве D₁ определена функция , которая называется сложной функцией от x (суперпозицией заданных функций).

Например, функция является суперпозицией двух функций и .

 

6.2. Преобразования графиков функций.

1. График функции 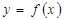можно построить с помощью преобразований (сдвиг, растяжение) графика некоторой уже известной функции.

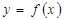1) График функции получается из графика функции сдвигом вдоль оси на 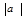единиц (вверх, если , и вниз, если ).

2) График функции 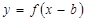получается из графика функции 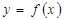сдвигом вдоль оси на единиц (вправо, если , и влево, если ).

3) График функции 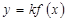получается из графика функции 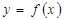растяжением вдоль оси в раз.

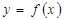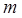4) График функции получается из графика функции сжатием по оси в раз.

5) График функции получается из графика функции 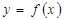симметричным отражением относительно оси .

6) График функции получается из графика функции 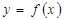симметричным отражением относительно оси .

 

 

Исследование функции с помощью производной

Определение:Точка х₀ называется точкой локального максимума, если для любого х из окрестности точки х₀ выполняется неравенство:

.

Определение:Точка х₀ называется точкой локального минимума, если для любого х из окрестности точки х₀ выполняется неравенство:

.

Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.

Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная 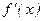обращается в нуль или терпит разрыв.

 

6.4. Правило нахождения экстремумов функции с помощью первой производной

1. Найти производную функции .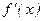

2. Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.

3. Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции 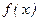. Если на промежутке , то на этом промежутке функция убывает; если на промежутке 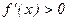, то на этом промежутке функция возрастает.

4. Если в окрестности критической точки 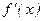меняет знак

с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.

5. Вычислить значения функции в точках минимума и максимума.

 

С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.

Пример 1: Найти промежутки монотонности и экстремумы функции: .

 

Решение: Найдем первую производную функции .

Найдем критические точки по первой производной, решив уравнение

Исследуем поведение первой производной в критических точках и на промежутках между ними.

 

		0		2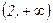
	+	0	-	0	+
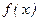
		т. max		т. min -4

Ответ: Функция возрастает при ;

функция убывает при ;

точка минимума функции ;

точка максимума функции .

 

6.5. Правило нахождения экстремумов функции