 |
Главная |
Основы теории подобия и моделирования
|
из
5.00
|
Основная трудность, возникающая при экспериментальном исследовании конвективного теплообмена, заключается в том, что коэффициент теплоотдачи зависит от многих параметров. Например, средний по поверхности коэффициент теплоотдачи от продольно омываемой пластины (см. рис. 9.2) зависит от длины пластины l, скорости набегающего потока ωж и теплофизических параметров жидкости:



Если проводить эксперименты, изменяя m раз каждый из шести параметров, влияющих на теплообмен, то суммарное число экспериментов будет N = m6, т.е. порядка 106.
Теория показывает, что число параметров зависит от выбора единиц измерения. Наименьшее число параметров получится, если единицы измерения будут связаны с самой решаемой задачей. Так, в качестве единицы длины можно принять не метр, а длину пластины l. Для перевода всех параметров в «новую» систему единиц измерения поделим их на l в той же степени, в которой длина входит в их размерность:
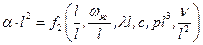
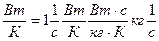
Число параметров в правой части уравнения уменьшилось, так как  , т.е. мы избавились от того параметра, который приняли за единицу измерения. Если теперь ввести ещё три «новых» единицы измерения: для времени t2/v, для массы
, т.е. мы избавились от того параметра, который приняли за единицу измерения. Если теперь ввести ещё три «новых» единицы измерения: для времени t2/v, для массы  и, наконец, для отношения тепловой мощности к перепаду температур
и, наконец, для отношения тепловой мощности к перепаду температур 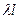 (в рассматриваемой системе величин единицы Вт и К раздельно не встречаются, а входят лишь в комбинации Вт/К), то в правой части рассматриваемой зависимости останется всего два безразмерных параметра:
(в рассматриваемой системе величин единицы Вт и К раздельно не встречаются, а входят лишь в комбинации Вт/К), то в правой части рассматриваемой зависимости останется всего два безразмерных параметра:
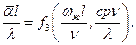
Такие же безразмерные параметры получаются и при анализе теплоотдачи от поверхности трубы, но определяющим размером в них будет не длина  , а диаметр d, соответственно внутренней – при течении жидкости внутри трубы и наружный – при наружном обтекании одной трубы или пучка труб.
, а диаметр d, соответственно внутренней – при течении жидкости внутри трубы и наружный – при наружном обтекании одной трубы или пучка труб.
Согласно основной теореме метода анализа размерностей (π-теореме) зависимость между N размерными величинами, определяющими данный процесс, может быть представлена в виде зависимости между составными из них N – K безразмерными величинами, где K – число первичных переменных с независимыми размерностями, которые не могут быть получены друг из друга. В уравнении  общее число переменных (включая и α) равно 7, из них четыре первичных (их мы принимали за единицы измерения) соответственно безразмерных чисел в уравнении
общее число переменных (включая и α) равно 7, из них четыре первичных (их мы принимали за единицы измерения) соответственно безразмерных чисел в уравнении 
N – K = 7 – 4 = 3.
Каждый из безразмерных параметров имеет определенный физический смысл. Их принято обозначать первыми буквами фамилии ученых, внесших существенный вклад в изучение процессов теплопереноса и гидродинамики, и называть в честь этих ученых.
Число Нуссельта : 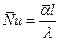
представляет собой безразмерный коэффициент теплоотдачи.
Число Рейнольдса : 
выражает отношение сил инерции (скоростного напора)  к силам вязкого трения
к силам вязкого трения 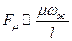 .
.
Безразмерные комплексы обычно не являются точным отношением каких-то сил, а лишь качественно характеризуют их соотношение. В данном случае сила вязкого трения между соседними слоями движущейся в пограничном слое жидкости, действующая на единичную площадку, параллельную плоскости y=0, равная по закону Ньютона Fµ =µ(𝜕ω/𝜕y). Заменяя производную отношением конечных разностей (𝜕ω/𝜕y) ≈ 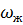 /δг получим Fµ ≈µωж/δг, где δг – толщина гидродинамического пограничного слоя. Принимая во внимание, что δг~
/δг получим Fµ ≈µωж/δг, где δг – толщина гидродинамического пограничного слоя. Принимая во внимание, что δг~ 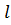 , получаем выражение Fµ ≈µωж/
, получаем выражение Fµ ≈µωж/ 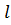 .
.
При малых числах Re преобладают силы вязкости и режим течения жидкости ламинарной (отдельные струи потока не перемешиваются, двигаясь параллельно друг другу, и всякие случайные завихрения быстро затухают под действием сил вязкости). При турбулентном течении в потоке преобладают силы инерции, поэтому завихрения интенсивно развиваются. При продольном обтекании пластины (см. рис. 10.1) ламинарное течение в пограничном слое нарушается на расстоянии xкр от лобовой точки, на котором

При течении жидкостей в трубах ламинарный режим на стабилизированном участке наблюдается до 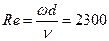 , а при Re >104 устанавливается развитый турбулентный режим (здесь d – внутренний диаметр трубы).
, а при Re >104 устанавливается развитый турбулентный режим (здесь d – внутренний диаметр трубы).
Число Прандтля :

состоит из величин, характеризующих теплофизические свойства вещества и по существу само является теплофизической константой вещества. Значение числа Pr приводится в справочных таблицах.
В случае естественной конвекции скорость жидкости вдали от поверхности ωж = 0 и соответственно Re = 0, но на теплоотдачу будет влиять подъемная сила Fп. Это приведет к появлению другого безразмерного параметра – числа Грасгофа:
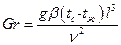
Оно характеризует отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.
При исследовании локального теплообмена кроме безразмерных чисел в уравнения войдут безразмерные координаты, представляющие собой
отношение обычных координат к определяющему размеру. Для продольно омываемой пластины это будет X = x/l.
Основная сложность метода анализа размерностей заключается в том, что нужно знать все параметры, влияющие на искомую величину. Для совершенно неисследованных процессов эти параметры находят, проводя предварительные эксперименты. Если же процесс уже описан математически, хотя бы на уровне дифференциальных уравнений, то в эти уравнения, в граничные и начальные условия к ним, очевидно, входят все влияющие на процесс параметры. Приводя к безразмерному виду математическое описание процесса, получают те же самые безразмерные числа. Этим занимается теория подобия. И, наконец, если даже задача решена аналитически, то и в этом случае для удобства анализа построения номограмм решения часто приводят к безразмерному виду. Например, построить графическую зависимость теплового потока через цилиндрическую стенку от всех влияющих на него параметров очень сложно, а зависимость в безразмерной форме Q/[λl(tc1 – tc2)] = f(d2/d1) выразится с помощью единственной линии.
|
из
5.00
|
Обсуждение в статье: Основы теории подобия и моделирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

