 |
Главная |
Понятие об элементарной плоской турбинной ступени. Геометрические характеристики турбинной решетки
|
из
5.00
|
Каждый из лопаточных венцов (направляющий и рабочий) представляет собой кольцевую решетку. Течение пара в ступени, состоящий из двух кольцевых решеток, одна из которых неподвижна, а другая вращается с угловой скоростью ω, имеет весьма сложный характер, параметры пара (давление, температура, объем и др.), являются функцией трех координат. В теории турбин координатными осями принято считать осевое направление (ось вращения турбины), радиальное направление и окружное направление.
Однако многие задачи теории турбин можно решить на основе упрощенного представления характера течения пара, рассматривая изменения параметров пара лишь вдоль одной оси, то есть на основе представления парового потока как одномерного. Изменением параметров пара относительно других осей пренебрегают. В осевых турбинах (пар движется вдоль оси вращения) этой осью считают ось вращения турбины, полагая, что в плоскости, перпендикулярной оси вращения, в любой момент времени значения параметров пара одинаковые. При таком упрощенном потоке пара, возможно, использовать закономерности термо- и газодинамики.
 Изложенное упрощенное одномерное течение рабочего тела в турбинной ступени формулируют как гипотезу плоских сечений профессора Н.Е.Жуковского, согласно которой течение пара в проточной части турбины происходит концентрическими цилиндрическими слоями, не смешивающимися между собой. Гипотеза позволяет рассматривать не весь поток пара по высоте канала, а течение пара в одном цилиндрическом сечении (слое).
Изложенное упрощенное одномерное течение рабочего тела в турбинной ступени формулируют как гипотезу плоских сечений профессора Н.Е.Жуковского, согласно которой течение пара в проточной части турбины происходит концентрическими цилиндрическими слоями, не смешивающимися между собой. Гипотеза позволяет рассматривать не весь поток пара по высоте канала, а течение пара в одном цилиндрическом сечении (слое).
Поэтому достаточно рассмотреть поток в одном таком «слое» для того, чтобы вынести суждение обо всем потоке. Вырезая мысленно один «слой», лежащий на среднем диаметре ступени и разворачивая его на плоскость, получим плоский (двухмерный) поток в системе из двух решеток. Одна из этих решеток неподвижна, а другая движется с окружной скоростью u, определяемой выражением:
u=ω  (2.1.)
(2.1.)
где ω – угловая скорость вращения турбины (с-1);
n – частота вращения ротора турбины (об/мин);
D – средний диаметр венца рабочих лопаток (м). Схема одной плоской решетки турбинных лопаток показана на рисунке 5.
Такое упрощенное представление потока в ступени носит название гипотезы плоских сечений, а система, состоящая из двух плоских решеток (неподвижной и подвижной) называется элементарной плоской турбинной ступенью.
 Для того чтобы характеризовать геометрию решетки турбинных лопаток задают ряд параметров, называемых геометрическими характеристиками решетки. К числу геометрических характеристик относятся (рис.6 и 7):
Для того чтобы характеризовать геометрию решетки турбинных лопаток задают ряд параметров, называемых геометрическими характеристиками решетки. К числу геометрических характеристик относятся (рис.6 и 7):
Ось решетки – ось АБ перпендикулярная оси вращения турбины.
Толщина профиля – диаметр наибольшей окружности, вписанной в профиль S.
Толщина кромки – толщины входнойS1 и выходнойS2 кромок профиля.
Форма профиля – это поперечное сечение лопатки. В настоящее время в турбинах используются заранее отобранные высоко эффективные стандартные профили. Поэтому форма профиля обычно задается его условным обозначением или маркой. При изменении размеров форма профиля остается неизменной, т.е. геометрическое подобие сохраняется. На рисунке 6 показаны формы профиля а) активного и б) реактивного типов турбинных лопаток.
Размеры лопаткихарактеризуются высотой лопатки ℓ и ходовой профиля в. Хордой называется максимальный размер профиля по направлению касательной к входной и выходной кромкам. 
Положение лопатки в решетке характеризуется шагом t и углом установки βв. Шаг решетки t определяется расстоянием между двумя соответствующими точками соседних профилей. Угол установки βв определяется углам между хордой профиля и плоскостью вращения рабочего колеса турбин.
В качестве геометрических характеристик используется также относительные величины: относительный шаг 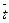 и относительная высота лопаток
и относительная высота лопаток  :
:
Две решетки являются геометрически подобны, если они составлены из профилей одинаковой формы, имеют одинаковые относительный шаг 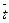 , угол установки βв и относительную высоту лопаток
, угол установки βв и относительную высоту лопаток  .
.
3. Преобразование энергии пара в активной и реактивной турбинных ступенях
а). Преобразование энергии пара в активной турбинной ступени
Пусть изображенные на рис.8 решетки относятся к активной турбинной ступени. Пар поступает в направляющую (сопловую) решетку с давлением Ро. Скорость пара на входе в сопла близка к нулю. Сопловые каналы выполняются сходящимися, поэтому при течении через направляющую решетку давление пара падает, а скорость возрастает (потенциальная энергия пара преобразуется в кинетическую энергию). На выходе из сопловой решетки давление пара равно Рd, а его скорость равна С1. Направление скорости С1 характеризуется углом α1, между вектором  и плоскостью вращения турбины, впредь которые будем называть:
и плоскостью вращения турбины, впредь которые будем называть:
С1 – абсолютная скорость выхода пара из направляющего аппарата (из сопел);
α1 – угол выхода пара из направляющего аппарата (из сопел).
Пройдя осевой зазор δαмежду обеими решетками, пар поступает в рабочую решетку. Но, рассматривая течение пара в рабочих лопатках, следует иметь в виду, что они вращаются вместе с ротором. Применительно к схеме рис.8 это означает, что рабочая решетка движется с окружной скоростью u. Скорость u по отношению к движению пара является переносной скоростью. Вычитая из вектора  вектор
вектор  , получим вектор
, получим вектор  , определяющий относительную скорость пара на входе в рабочую решетку. Направление скорости W1 характеризуется углом β1.
, определяющий относительную скорость пара на входе в рабочую решетку. Направление скорости W1 характеризуется углом β1.
 Заметим, что когда, говорится о течении пара через каналы рабочей решетки, имеет смысл рассматривать только относительное движение пара, т.е. связывать оси координат с вращающимися рабочими лопатками. Если на рабочих лопатках поместить наблюдателя с измерительными приборами, то эти приборы во входном сечении решетки зарегистрируют скорость W1 и угол β1.
Заметим, что когда, говорится о течении пара через каналы рабочей решетки, имеет смысл рассматривать только относительное движение пара, т.е. связывать оси координат с вращающимися рабочими лопатками. Если на рабочих лопатках поместить наблюдателя с измерительными приборами, то эти приборы во входном сечении решетки зарегистрируют скорость W1 и угол β1.
Впредь будем называть:
W1 – относительная скорость входа пара в рабочую решетку;
β1 – угол входа пара в рабочую решетку.
Треугольник, образованный векторами  ,
,  и
и  называется входным треугольником скоростей. Отметим, что скорость С1 иногда называют абсолютной скоростью пара, подчеркивая, что эта скорость измеряется в координатах, связанных с неподвижной направляющей решеткой. Отметим также, что отсчет углов входного треугольника α1 и β1 производится от оси, направление которой совпадает с направлением движения лопаток.
называется входным треугольником скоростей. Отметим, что скорость С1 иногда называют абсолютной скоростью пара, подчеркивая, что эта скорость измеряется в координатах, связанных с неподвижной направляющей решеткой. Отметим также, что отсчет углов входного треугольника α1 и β1 производится от оси, направление которой совпадает с направлением движения лопаток.
В активной ступени, где импульс потока пара непосредственно передается лопатками, скорость W1 должна быть достаточно большой, а ее направление – близким к направлению движения лопаток, т.е. угол β1 должен быть небольшим. Это возможно только в том случае, если скорость пара С1 существенно больше окружной скорости лопаток. Другими словами, поток пара необходимо «разогнать» в направляющем аппарате до такой скорости, которая обеспечила бы активное воздействие струи пара на движение лопатки.
Построение входного треугольника скоростей позволило перейти от «абсолютного» к относительному движению пара. Пар поступает на рабочие лопатки со скоростью W1 (в осевом зазоре скорость практически не меняется). Поскольку ступень активная (каналы между рабочими лопатками имеют постоянное сечение), то давление и скорость пара при течении через рабочую решетку не меняется – в относительном движении лопатки неподвижным и пар не совершает работы. Поэтому давление Р1, за рабочей решеткой равно давлению перед решеткой Рd, а скорость пара W2 за рабочей решеткой близка к скорости входа W1. (В действительности все же скорость W2 будет незначительно меньше W1, из–за трения). Но направление потока пара резко изменяется – пар выходит из решетки под углом β2 к плоскости вращения турбины.
Впредь будем называть:
W2 – относительная скорость выхода пара из рабочей решетки;
β2 – угол выхода пара из рабочей решетки.
Для того чтобы вернуться к «абсолютному» движению пара необходимо к вектору относительной скорости  прибавить вектор окружной скорости
прибавить вектор окружной скорости  , выполнив сложение, получим скорость пара за ступенью
, выполнив сложение, получим скорость пара за ступенью  и угол α2. Треугольник, образованный векторами
и угол α2. Треугольник, образованный векторами  ,
,  и
и  называется выходным треугольником скоростей.
называется выходным треугольником скоростей.
Подчеркнем, что отсчет углов выходного треугольника β2 и α2 производится от оси, направление которой противоположно направлению движения лопаток. Поэтому в активной решетке, где каналы имеют постоянное сечение, угол β2 по своей величине оказывается близким к углу β1.
Из треугольников скоростей видно, что абсолютная скорость пара и его кинетическая энергия при течении через рабочую решетку резко уменьшается: от скорости С1 перед рабочими лопатками до скорости С2 за рабочими лопатками, т.к. на рабочих лопатках осуществляется преобразование кинетической энергии пара в механическую работу вращения вала турбины.
 Обычно при построении треугольников скоростей их вершины совмещают в одной точке, называемой полюсом. На рис.8 показано такое построение, причем форма треугольников характерна именно для активной ступени. Подчеркнем особенности треугольников скоростей активной ступени:
Обычно при построении треугольников скоростей их вершины совмещают в одной точке, называемой полюсом. На рис.8 показано такое построение, причем форма треугольников характерна именно для активной ступени. Подчеркнем особенности треугольников скоростей активной ступени:
– величина скорости пара W2 на выходе из рабочей решетки близка к скорости пара на входе W1;
– угол выхода потока β2. близок к углу входа β1., т.к. рабочие лопатки симметричны;
– скорость пара С1 существенно больше окружной скорости лопаток u
– скорость С1 больше чемW2 .
Таким образом, в активных ступенях четко выражены два этапа преобразования энергии пара. В направляющем аппарате осуществляется преобразование потенциальной энергии пара в кинетическую; давление пара падает, а скорость возрастает. На рабочих лопатках потенциальная энергия пара не изменяется, а кинетическая энергия преобразуется в механическую работу; давление пара остается неизменным, а его скорость (в «абсолютном» движении) падает от значения С1 до значения С2.
|
из
5.00
|
Обсуждение в статье: Понятие об элементарной плоской турбинной ступени. Геометрические характеристики турбинной решетки |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

