КОНТРОЛЬНАЯ РАБОТА № 2. Пример к задаЧе 2.1

Пример к задаЧе 2.1.

 

Для заданного поперечного сечения состоящего из швеллера №12 и двутавра №18 требуется:

1. Определить положение главных центральных осей инерции и вычислить соответствующие осевые моменты инерции.

2. Построить эллипс инерции и определить направления наибольшей и наименьшей жесткости балки на изгиб.

При расчетах использовать таблицы сортамента (части стандартных профилей прямоугольниками не заменять). Сечение и эллипс вычертить в масштабе 2:1, изобразить начальные, промежуточные и главные центральные оси.

 

РЕШЕНИЕ

Рис.1

 

Сечение (рис.1) состоит из швеллера № 12 и двутавра № 18.

 

1. Разбиваем сечение на отдельные фигуры:

 

Фигура 1 – швеллер № 12

В таблице сортамента приведены геометрические характеристики для швеллера, расположенного вертикально:

 

 

h1 = 12 см, b1 = 5,2 см; = 1,54 см А = 13,3 см2, 304 см4; 31,2 cм4; Jxy = 0 (оси х,у – главные)

В нашем примере швеллер расположен горизонтально (рис.1), поэтому

31,2 см4 304 см4

y

Оси х₁ и у₁ по сравнению с табличными осями поменялись местами.

 

Фигура 2 – двутавр № 12

b	h2 = 18 см, b2 = 9 см, А = 23,4 см2, 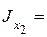1290 см4; 82,6 cм4, Jxy = 0 (оси х,у – главные)

 

2. Найдем координаты центра тяжести всего сечения в произвольной системе координат XОY. Систему координат XОY выбираем сами, таким образом, чтобы можно было легко определить координаты центров тяжести каждой из двух фигур.

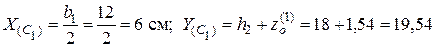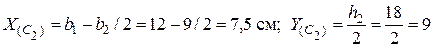см

см

Замечание: в зависимости от выбора системы XОY знаки величин могут быть и отрицательными.

Обозначим далее и т.д.

Определим координаты центра тяжести всего сечения т.С и построим центральные оси X_с,Y_с, параллельные исходным осям X,Y.

Полученную точку С(X_CY_C) наносим на рис.1 и строим центральные оси X_CY_C.

Замечание: если весь чертеж выполнен в масштабе, то точка С должна лежать на прямой, соединяющей точки С₁ и С₂.

Обозначим далее А = А₁ + А₂ = 13,34 + 23,4 = 36,74 см².

3. Вычислим моменты инерции всего сечения относительно осей Х, У.

 

4. Подсчитаем моменты инерции сечения относительно центральных осей X_C ,Y_C. Используем формулы параллельного переноса для случая перехода от произвольных осей фигуры к центральным (знаки "минус"):

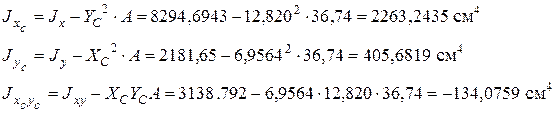
Замечание: 1) Осевые моменты инерции всегда должны получаться положительными; 2) если точки С₁ и С₂ лежат в первой и третьей четвертях системы X_CY_C, то центробежный момент должен получаться положительным (см.рис.1). Если во II и IV - то отрицательным.

 

5. Определим положение главных центральных осей X_глY_гл.

Так ¹ 0, то оси X_CY_C – центральные, но не главные.

Необходимо найти угол b наклона оси X_гл к оси X_С.

b > 0 от оси Хс к Хгл против часовой стрелки b < 0 – по часовой стрелке

Угол b определяем из выражения .

Имеем .

2b = arctg (0,1444) = 8°13¢

b = 4°06¢

Строим оси X_глY_гл - рис.1.

 

6. Подсчитаем главные моменты инерции сечения, пользуясь формулами поворота осей на угол b

Проверка:

1. Большее значение (в нашем случае это = 2263.2435 cм⁴ "переходит" в еще большее ( = 2272.8644 см⁴), а меньшее ( = 405.6819см⁴) "переходит" в еще меньшее ( = 396.0610 см⁴).

2. Должно выполняться условие .

2263.2435 + 405.6819 = 2272.8644 + 396.0610

2668.9254 = 2668.9254

3. должно равняться нулю.

=

½ (2263.2435 – 405.6819)sin 8°13¢ - 134.0759 cos 8°13¢ = 0.3885 » 0

 

7. Построим эллипс инерции сечения.

Полуоси эллипса, называемые радиусами инерции:

- откладываем по У_гл

 

- откладываем по оси Х_гл

На этих осях строим эллипс инерции (рис.1).

Выводы: Положение главных центральных осей X_гл и Y_гл показано на рис.1. Главные моменты инерции сечения: = 2272.8644 см⁴, =396.0610 см⁴.

Положение эллипса инерции сечения говорит о том, что при изгибе балки в направлении оси Y_гл ее жесткость и прочность будут наибольшими, а при изгибе в направлении X_гл - наименьшими.

 

Замечание: Если заданное сечение содержит стандартный уголок, расчет выполняется аналогично.

Рисуем уголок отдельно, пусть уголок 50х50х3. Выписываем из сортамента геометрические характеристики

b = 5 см; z0 = 1,33 см; A = 2,46 см2; Jx = Jy = 7,11 см4; Jmax = 11,31 см4; Jmin = 2,95 см4

Для уголка оси х,у не являются главными, поэтому центробежный момент инерции не равен нулю, а определяется по формуле

.

Знак плюс или минус определяется в зависимости от взаимного расположения уголка по отношению к осям х, у (см.рис.2).

В нашем случае «минус» т.к. большая часть сечения (на рисунке она заштрихована) расположена во 2-ой и 4-ой четвертях, где х,у< 0 ( )

см⁴ ¹ 0,

в отличие от двутавра и швеллера, у которых J_ху = 0.

 

y x

y > 0 x

< 0 y x

Pис.3

 

ПРИМЕР ЗАДАЧЕ 2.2

 

Для заданной схемы балки (рис.1) при Р = 12 кН, m = 12 кН×м, q=12 кН м, a = b= c = 1,5 м, [s] = 0,8 кН/см², [t] = 0,4 кН/см².

Требуется:

1. Построить эпюры Q_y и M_x .

2. Подобрать деревянную балку

а) круглого сечения,

б) прямоугольного, приняв h/b = 2.

 

Решение

Рис.1

 

1. Определяем реакции опор R_A и R_B. Записываем сумму моментов относительно точек А и В, в которых находятся опоры:

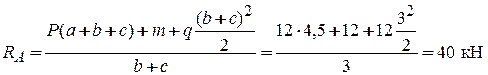
Проверка

2. Выражения для внутренних поперечных сил Q_y и внутренних изгибающих моментов М_х для каждого из трех участков балки получаем методом сечений. Мысленно проводим сечение. Отбрасываем часть балки либо слева, либо справа от сечения. Действие отброшенной части заменяем внутренними силовыми факторами Q_y и М_х, которые находим из уравнений статики.

Для левой части (отброшена правая):

Q_y направлена вниз по оси У; М_х

М_х против часовой стрелки. Q_y

Для правой части (отброшена левая): Q_y

Q_y направлена вверх; M_x

М_х по часовой стрелки.

Для определения Q_y и М_х рисуем отдельно выбранную для расчета часть, указываем всю внешнюю нагрузку, направление внутренних силовых факторов Q_y и М_х и определяем их из уравнений статики: åY =0, åМ_х = 0 (сумма проекций всех сил на ось Y и сумма моментов всех сил относительно точки С, в которой провели сечение).

1-й участой 0 £ z £ a (левая часть)

z Qy	å Y = 0 Qy + P = 0 Qy = -P å Mx Mx + Pz = 0 Mx = -Pz

2-й участой a £ z £ a + b (левая часть)

z a Qy Mx q RA P

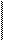
å Y = 0 Qy + P - RA + q(z - a) = 0 Qy = - P + RA - q(z - a) å Mx=0 Mx + q(z - a)2/2 - RA(z - a) + Pz = 0 Mx = - q(z - a)2 /2 + RA(z - a) + Pz = 0

3-й участой c ³ s ³ 0 (правая часть)

RB	å Y = 0 -Qy - RB + qs = 0 Qy = -RB + qs å Mx = 0 - Mx - qs2/2 + RBs = 0 Mx = - qs2/2 + RBs

Строим графики эпюры Q_y и М_х под расчетной схемой конструкции (рис.1). На расчетной схеме должны быть указаны найденные значения опорных реакций R_А и R_В, вся внешняя нагрузка. Положительные значения Q_y и М_х откладываем по направлению оси Y (вниз).

На участках, где действует распределенная нагрузка q, эпюра Q_y - наклонная прямая, эпюра М_х парабола выпуклостью вниз (если q направлена вниз). Скачки (разрывы) на эпюре Q_y могут быть только в точках, где приложены сосредоточенные силы или опорные реакции. Величина скачка равна величине приложенной силы. Скачки на эпюре моментов могут быть только в тех сечениях, где приложены сосредоточенные моменты. Величина скачка равна величине приложенного момента.

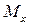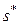Там где эпюра Q_y имеет нулевую точку, на эпюре М_х - экстремум (М_х = 2.67 кН×м, рис.1). Для определения экстремума надо приравнять нулю выражение Q_y на этом участке и получить из этого уравнения значение . Подставляя в выражение М_х на данном участке, получим значение экстремума М_х. В нашем примере , на 3-ем участке м. Подставляя в выражение на данном участке, получим кН×м.

3. Подбор деревянной балки круглого сечения.

Условие прочности балки по нормальным напряжениям s_z имеет вид:

(1)

c перегрузкой не более 5 % и недогрузкой не более 15 %.

Величина ½ М_х ½_max определяются по эпюре М_х и в нашем случае есть ½М_х½_max = 18 кН×м = 1800 кН×см.

Из (1) см³.

Момент сопротивления круглого сечения есть cм³ , откуда получаем

R = 14,2 см .

Проверим условие прочности балки по максимальным касательным напряжениям в сечении у = 0:

(2)

с перегрузкой не более 5 % и любой недогрузкой.

½Q_y½_max = 28 кН - по эпюре Q_y; - момент инерции для круга;

b= 2R - ширина сечения на уровне у = 0, где действуют ½t_zy½_max ;

- статический момент площади полукруга, расположенной ниже уровня, где действуют ½t_zy½_max .

В нашем случае .

А_отс – площадь полукруга; У_отс – центр тяжести полукруга.

Полагая R = 14,2 см, по формуле (2) получаем ½t_zy½_max = 0,177 кН/см² при допускаемом напряжении [t] = 0,4 кН/см².

Следовательно, условия прочности балки выполняются и для данной схемы подходит деревянная балка диаметром D = 28,4 см. Площадь поперечного сечения 633,150 см².

4. Подбор деревянной балки прямоугольного сечения с отношением сторон h/b = 2 (h - высота, b - основание).

Аналогично предыдущему , W_x = 2250 cм³.

Для прямоугольного сечения .

Тогда при h = 2b имеем см³ ;

см; см

Максимальные касательные напряжения в сечении у = 0 определяются по формуле (2):

½Q_y½_max = 28 кН; = 33302 cм⁴; b = 14,95 см;

1671 см³

А_отс – площадь половины прямоугольника; У_отс – центр тяжести.

Тогда (2) ½t_zy½_max = 0,094 кН/см² при [t] = 0,4 кН/см².

Условие прочности балки выполняются и для данной схемы подходит деревянная балка прямоугольного сечения A=b ´ h = 15 см ´ 30 см=450 см².

Площадь прямоугольного сечения оказалась значительно меньше площади круглого сечения, что приводит к экономии материала.

ПРИМЕР К ЗАДАЧЕ 2.3.

Для заданной схемы балки при Р = 100 кН; m = 30 кН×м; q = 10 кН/м; l = 4 м; a = 0.5 l₁ = 2 м; l₂ = 2 м требуется:

1. Написать выражения Q_y и М_х для каждого участка, построить эпюры и подобрать стальную балку двутаврового профиля [s] =16 кН/см², [t] =8 кН/см².

2. Записать дифференциальное уравнение изогнутой оси балки для каждого участка, выполнить интегрирование и построить эпюры углов поворота сечений и прогибов.

3. Проверить балку на жесткость при допускаемом прогибе [f]=l/150, где l - длина балки. Е = 2×10⁴ кН/см².

 

Решение

Рис.1

1. Для консольной балки строим эпюры, не определяя опорных реакций в заделке. Идем со свободного конца:

1 участок 0 £ z £ l₁

z m q Qy Mx

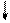
å Y = 0 Qy + qz = 0 Qy = - qz å Mx = 0 Mx + qz2/2 - m = 0 Mx = - qz2/2 + m

2 участок l₁ £ z £ l₁ + l₂

z l1 Qy Mx P q m

å Y = 0 Qy + ql1 + P = 0 Qy = - ql1 – P å Mx = 0 Mx + P(z - l1) + ql1(z - l1/2) - m = 0 Mx = - P(z - l1) - ql1(z - l1/2) + m

Строим эпюры Q_y и М_х под расчетной схемой конструкции (рис.1).

2. Подбор двутавра. По эпюрам Q_y и М_х определяем положение опасных сечений и соответствующие расчетные значения силовых факторов

½M_х½_max= 50 кН×м в сечении z = 4 м,

½Q_y½_max = 30 кН на 2-ом участке.

Запишем условие прочности по максимальным нормальным напряжениям:

Отсюда

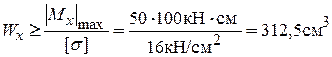
Из таблицы сортамента находим значение =317см³, соответствующее двутавру № 24а.

	b

 

 

Выпишем из таблицы геометрические характеристики двутавра № 24а и проверим его прочность по максимальным нормальным ½s_z½_max и максимальным касательным ½t_zy½_max напряжениям.

 

Двутавр № 24: h = 24 см; J_x = 3800 см⁴ ; W_x = 317 см³ ; S_x = 178 см³;

d = 0,56 см

Максимальное нормальное напряжение

Недогрузка .

Условие прочности по s_{z max} выполняется. Недогрузка 1,25 %.

Максимальные касательные напряжения в сечении у =0.

d – толщина стенки двутавра на уровне у =0.

Здесь допустима любая недогрузка (перегрузка не более 5 %).

Ответ: Двутавр № 24а удовлетворяет условиям прочности по s_{z max} и t_{z max} .

 

3. Дифференциальное уравнение изгиба 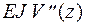= - M_x

V (z) - перемещение оси балки по направлению оси Y,

Е - модуль Юнга,

J_x - момент инерции сечения балки.

В соответствии с методом Клебша продолжим нагрузку q до правого конца балки и добавим снизу компенсирующую нагрузку - q (рис.1). Внешний момент m будет записываться в виде m(z - a)^o, где а - координата по оси z точки приложения момента. Интегрируем дважды не раскрывая скобок.

1 участок 0 £ z £ l₁

2 участок l₁ £ z £ l₁ + l₂

Для определения постоянных интегрирования C и D используем условия закрепления балки.

В заделке при l = 4 м угол поворота V¢(l) = 0 и прогиб V(l) = 0

= 0.

Отсюда С = 6 (кН×м²).

= 0.

D = 103 (кН×м³).

Подставляя найденные значения С и D в выражения для EJV¢(z) и EJV(z) вычисляем для каждой точки z соответствующее значение углов поворота и прогибов умноженных на константу EJ_x. Строим эпюры EJV¢(z) и EJV(z), под эпюрами Q_y и М_х. Все четыре эпюры связаны дифференциальными зависимостями.

 

4. Проверим жесткость балки. Двутавр № 24а : Е = 2×10⁴ кН/см²,

J_x = 3800 cм⁴ .

Условие жесткости V_max £ [f]

Допускаемое значение прогиба см

По эпюре EJV(z) берем максимальное значение EJV_max = 107 кН×м³ = = 107×10⁶ кН×см³ .

(см)

Условие жесткости выполняется.

Двутавр № 24а подходит для данной конструкции и по прочности и по жесткости.