Функции отклика и их параметрическое исследование

При проведении натурного эксперимента измеряются параметры состояния конструкции в отдельных точках, в которых размещены датчики. Статические испытания предполагают, что показания датчиков зависят только от неизменных во времени (или медленно изменяющихся) параметров состояния. Так, датчики перемещений дают возможность измерить перемещения в отдельных точках конструкции; тензодатчики деформаций дают значение деформации на некоторой базе, которая фактически является осредненной по длине датчика компонентой деформации вдоль его длины. Таким образом, вектор показаний всех датчиков в некоторый момент времени (на определенной стадии эксперимента) можно, вообще говоря, выразить через поля перемещений конструкции, которые в дискретной модели аппроксимируются с помощью вектора узловых значений. Примем эту связь линейной:

(2.117)

Здесь Z – вектор показаний датчиков,

q* – вектор узловых перемещений,

С – матрица связи.

Перемещения q* в равенстве (2.117) – это значения перемещений, фактически реализуемые в натурной конструкции во время эксперимента, в точках, совпадающих с узлами конечно-элементной модели. Фактические перемещения q* и рассчитанные перемещения q отличаются на величину невязки, которая обусловлена различиями в приложении нагрузки, случайными отклонениями конструктивных параметров и неточностью задания физико-механических параметров материалов. Предполагая, что наибольший вклад в эту разность дают физико-механические параметры, найдем их из условия минимума взвешенной невязки [87, 92]:

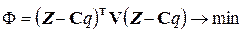, (2.118)

где V – диагональная матрица весовых коэффициентов.

В данном случае рассчитанные перемещения q зависят от варьируемых параметров, которые пока неизвестны и подлежат определению.

Заметим, что в функционале (2.118) векторы Z и q могут включать значения нескольких измерений, при разных нагрузках, что позволяет увеличить число измеряемых величин при одной и той же схеме расположения датчиков.

Дифференцируя (2.118) по варьируемым параметрам и приравнивая результат к нулю, получаем:

(2.119)

В системе уравнений (2.119) число уравнений равно числу датчиков, а число неизвестных параметров состояния q– числу степеней свободы дискретной модели конструкции, т.е. во много раз больше. Таким образом, полученная задача математически некорректна и требует регуляризации.

Применим искусственный прием, состоящий в использовании вместо матричного уравнения статики уравнения движения конструкции с последующим переходом к стационарному случаю.

Уравнение движения конструкции, моделируемой конечно-элементной моделью, записываем в виде [87, 92]

. (2.120)

Соответственно составляем модель измерительной, например тензорезисторной, системы:

(2.121)

Здесь М, Ф и Н − матрицы соответственно инерционная, диссипативная и жёсткости конструкции; − вектор обобщённых координат; − вектор внешних воздействий; − заданные матрицы, зависящие от способа приложения нагрузки, числа и мест расположения датчиков.

В дальнейшем выражения (2.120) и (2.121) представляем в форме

(2.122)

(2.123)

Здесь введены обозначения: − вектор переменных состояния конструкции; , − переменные матрицы, не зависящие от ; (в дальнейшем знак ~ опускаем).

Полагаем, что конструкция наблюдаема в смысле Калмана [94]. Так, если − постоянные матрицы, условием наблюдаемости является равенство:

(2.124)

где r − символ операции определения ранга матрицы.

Критерий качества оценивания взят в форме критерия обобщенной работы [Буков, Шендрик], в виде [87, 92]

(2.125)

где − действительные показания датчиков системы измерения; 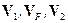− заданные симметричные определенно положительные матрицы весовых коэффициентов. Функционал (2.125) преобразуем к виду

(2.126)

Ставится задача о нахождении оценок переменных и усилий , доставляющих минимум функционалу (2.125).

Введем функцию

(2.127)

где 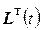− вектор "неопределенных множителей" Лагранжа.

Условия достижения минимума критерия (2.127) записываем в форме уравнений Эйлера:

(2.128)

Из первого условия (2.128) следует

(2.129)

из второго получаем

(2.130)

Уравнения (2.129) и (2.130) достаточны для отыскания оценок переменных и при заданных .

В дальнейшем оценки переменных состояния и возмущающих сил обозначаем , .

В зависимости от вида задачи уравнения (2.129) и (2.130) должны быть решены с учетом различных граничных условий.