 |
Главная |
ТЕМА № 2. ЛОГИКА ВЫСКАЗЫВАНИЙ
|
из
5.00
|
Высказывание. Простые и составные высказывания. Операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Таблицы истинности. Способы построения отрицания высказываний.
Литература: [1] с. 5-23; [2] с. 29-38; [3] с. 5-15; [4] с. 5-11; [5] с. 33-46; [6] с. 37-42; [7] с. 57-71.
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания 1 уровня)
1А. Какие из следующих предложений являются высказываниями? Для высказываний определите их значения истинности:
а) число 25 делится на 5;
б) 23+7;
в) 3>7;
г) Минск – столица Беларуси;
д) все числа делятся на 8.
1Б. Постройте отрицание высказывания Р и определите его значение истинности:
а) Р: «Число 105 делится на 3»;
б) Р: «Число 23 не делится без остатка на 3»;
в) Р: «В прямоугольнике все углы прямые»;
г) Р: «Квадрат является ромбом».
2А. Какие из следующих предложений определяют высказывания? Определите их значения истинности:
а) существуют хÎR, что х+2<5; б) сегодня хорошая погода;
в) ты любишь математику?; г) существуют простые числа.
2Б. Сформулируйте отрицания высказываний, встречающихся в начальной школе:
а) Алеша моложе Тани; б) масса кролика меньше массы гуся;
в) тетрадь дороже карандаша; г) красный отрезок длинней синего.
3А. Среди данных предложений укажите высказывания. Определите их значения истинности:
а) число 2 – простое;
б) слово «делится» является глаголом;
в) в каком году родился А.С. Пушкин?
г) лось является парнокопытным животным.
3Б. Найдите значения истинности высказываний А и В и объясните, почему они не являются отрицаниями друг друга:
а) А: «Слово «сад» – прилагательное»,
В: «Слово «сад» – наречие»;
б) А: «Все треугольники являются равнобедренными»,
В: «Все треугольники не являются равнобедренными»;
в) А: «Некоторые слова могут быть разделены на слоги»,
В: «Некоторые слова не могут быть разделены на слоги».
4А. Какие из следующих предложений являются высказываниями? Для высказываний определите их значения истинности:
а) на 0 делить нельзя; б) пусть всегда будет солнце!
в) 11–2=9; г) существуют хÎR, что х+3≥52.
4Б. Выясните какие из высказываний каждой пары являются отрицаниями друг друга:
а) А: «В книге 100 страниц», В: «В книге не более 100 страниц»;
б) А: «Эта гвоздика красная», В: «Эта гвоздика розовая»;
в) А: «Эта гвоздика красная», В: «Эта гвоздика не красная»;
г) А: «Данное слово − существительное»,
В: «Данное слово − прилагательное».
5А. Среди данных предложений укажите высказывания. Определите их значения истинности:
а) число а делится на 5;
б) существуют четные простые числа;
в) берегите мир!
г) некоторые высказывания не являются истинными.
5Б. Найдите значения истинности высказываний М и К и объясните, почему они не являются отрицаниями друг друга:
а) М: «Все студенты – отличники»,
N: «Все студенты – не отличники»;
б) М: «Некоторые числа записываются с помощью цифр»,
N: «Некоторые числа не записываются с помощью цифр»;
в) М: «25 – отрицательное число»,
N: «25 – четное число».
0А. Среди данных предложений укажите высказывания. Определите их значения истинности:
а) брусника – растение, характерное для хвойного леса;
Решение: Это высказывание. Оно истинно, т.к. брусника является растением, характерным для хвойного леса.
б) некоторые высказывания являются ложными;
Решение: Это высказывание истинно, т.к. нам известно, что существуют истинные высказывания и существуют ложные.
в) 25+х≤7;
Решение: Это предложение не является высказыванием, т.к. нельзя определить его истинность.
0Б. Постройте отрицание высказывания Q и определите его значение истинности:
а) Q: «Существуют инопланетные цивилизации»;
 : «Не верно, что существуют инопланетные цивилизации» (ложно).
: «Не верно, что существуют инопланетные цивилизации» (ложно).
б) Q: «Сумма внутренних углов треугольника равна 180о»;
Решение:`  : «Не верно, что сумма внутренних углов треугольника равна 180º» (ложно).
: «Не верно, что сумма внутренних углов треугольника равна 180º» (ложно).
в) Q: «Число 21 делится на 2»
Решение:  : «Не верно, что число 21делится на 2» (истинно).
: «Не верно, что число 21делится на 2» (истинно).
.
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания II уровня)
1А. Дано высказывание А: «0 – целое число». Приведите пример такого высказывания В, чтобы конъюнкция высказываний А и В была: а) истинной, б) ложной; чтобы импликация высказываний А и В была: в) истинной, г) ложной.
1Б. Выясните логическую структуру следующих высказываний и найдите их значения истинности:
а) число 5 – целое или положительное;
б) 16 кратно 2 и кратно 5;
в) если у параллелограмма АВСD все стороны равны, то этот параллелограмм – ромб.
2А. Дано высказывание С: «Число 3 больше числа 2 на 1». Можно ли привести пример такого высказывания D, чтобы конъюнкция высказываний С и D была: а) ложной, б) истинной; чтобы импликация высказываний С и D была: в) истинной, г) ложной.
2Б. Выясните логическую структуру следующих высказываний и найдите их значения истинности:
а) слово «группа» - прилагательное или глагол;
б) если число 12 кратно 4, то оно кратно 2;
в) число 7 – натуральное и однозначное.
3А. Дано высказывание В: «Число 7 – четное». Приведите пример такого высказывания С, чтобы дизъюнкция высказываний В и С была: а) истинной, б) ложной; чтобы импликация высказываний В и С была: в) истинной, г) ложной.
3Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значения истинности:
а) число 17 не делится на 5;
б) всякий равнобедренный треугольник прямоугольный и равносторонний;
в)  =2;
=2;
г) если число 42 делится на 2, то оно четное.
4А. Определите значения истинности высказываний А, В, D, если:
а) А Ù «В слове «стол» 4 звука» ≡ И;
б) «Вода в море пресная» Û В ≡ Л;
в) D Þ «При 0о вода замерзает» ≡ И.
4Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значения истинности:
а) число 13 простое и делится на 2;
б) 122 четное число или нечетное;
в) в прямоугольном треугольнике один из углов равен 90о;
г) если сумма цифр числа 75 делится на 3, то число делится на 3».
5А. Определите значения истинности высказываний Е, F, G, если:
а) Е Þ «Воздух хорошо проводит тепло» ≡ Л;
б) «Синус любого угла меньше 1» Û F ≡ И;
в) G Ú «Слово «река» – существительное» ≡ Л.
5Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значение истинности:
а) слово «пальто» не склоняется;
б) если арбуз – бахчевая культура, то Минск – столица Беларуси;
в) гипотенуза прямоугольного треугольника, вписанного в
окружность, является ее диаметром;
г) все реки текут.
0А. Выясните логическую структуру следующих высказываний и найдите их значение истинности:
а) «Если число 10 заканчивается цифрой 0, то оно делится на 5»;
Решение: АÞВ – импликация высказываний, где А – условие, В – заключение. А: «Число10 заканчивается цифрой 0» – истинно; В: «Это число делится на 5» – истинно. Тогда АÞВ – истинно по определению импликации.
б) «Карась – морская или речная рыба»;
Решение: АÚВ – дизъюнкция высказываний А: «Карась – морская рыба» - ложно. В: «Карась – речная рыба»- истинно. Тогда АÚВ – истинно по определению дизъюнкции.
в) «Число 13 четное и натуральное»;
Решение: АÙВ – конъюнкция высказываний. А: «Число 13 – четное» – ложно. В: «Число 13 – натуральное» – истинно. Тогда АÙВ – ложно по определению конъюнкции.
0Б. Определите значения истинности высказываний А, В, С, если:
а) «sin 90о = 0» Û А ≡ И;
Решение: Дана эквиваленция 2-х высказываний, которая истинна. Известно, что эквиваленция двух высказываний истинна при одинаковых значениях истинности входящих в него высказываний. А поскольку высказывание «sin 90о = 0» – ложно, то и высказывание А – ложно.
б) В Þ «тела при нагревании не расширяются» ≡ Л;
Решение: Дана импликация 2-х высказываний, которая ложна. Импликация двух высказываний истинна во всех случаях, кроме одного, когда первое высказывание истинно, а второе – ложно. Высказывание «тела при нагревании не расширяются» ложно, значит, высказывание В – истинно.
в) С Ù «укроп – растение семейства зонтичных» – И;
Решение: Дана конъюнкция 2-х высказываний. Конъюнкция высказываний истинна тогда и только тогда, когда истинны оба высказывания. Поскольку «укроп – растение семейства зонтичных» истинное высказывание, то высказывание С – истинно.
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания III уровня)
1А. Составьте таблицы истинности для высказываний:
а) (АÙВ)ÙС; б) 
1Б. Даны составные высказывания:
а) «Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А»;
б) «Числа m и n взаимно просты тогда и только тогда, когда у них нет общих делителей».
Запишите данные высказывания в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций.
2А. Составьте таблицы истинности для высказываний:
 а) АÙ
а) АÙ  , б) АÚВÞС.
, б) АÚВÞС.
2Б. Даны составные высказывания:
а) «Четырехугольник АВСD является параллелограммом тогда и только тогда, когда его противоположные стороны попарно параллельны»;
б) «Высказывание В является отрицанием высказываниz А тогда и только тогда, когда А и В принимают противоположные значения истинности».
Запишите каждое высказывание в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций.
3А. Составьте таблицы истинности для высказываний:
а) СÞ (АÙВ), б) АÞ (  ÚВ).
ÚВ).
3Б. Даны высказывания:
а) «3 и 8 – однозначные числа»;
б) «Собака – домашнее или дикое животное».
Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
4А. Составьте таблицы истинности для высказываний:
а) АÞ(АÙ  ), б) АÞ (
), б) АÞ (  ÙС).
ÙС).
4Б. Даны высказывания:
а) «Картофель и тыква – овощи»;
б) «Число 0,7 – натуральное или целое».
Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
5А. Составьте таблицы истинности для высказываний:
а) (  ÙВ) ÞС, б) АÞ(
ÙВ) ÞС, б) АÞ(  ÙВ).
ÙВ).
5Б. Даны высказывания:
а) «Число 17 – четное или делится на 5»;
б) «Свекла растет в поле и в огороде».
Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
0А. Составьте таблицы истинности для высказываний:
 а) АÙВ Þ
а) АÙВ Þ  , б)
, б)  Ú
Ú  ÞС.
ÞС.
Решение:
а) АÙВ Þ  ,
,
| А | В | С | АÙВ | 
| (АÙВ)Þ 
|
| и и и и л л л л | и и л л и и л л | и л и л и л и л | и и л л л л л л | л и л и л и л и | л и и и и и и и |
Решение:
 б)
б)  Ú
Ú  ÞС.
ÞС.
| А | В | С | 
| 
|  Ú Ú 
|  Ú Ú  ÞС ÞС
| |
| и и и и л л л л | и и л л и и л л | и л и л и л и л | л л л л и и и и | л л и и л л и и | л л и и и и и и | и и и л и л и л |
0Б. Даны составные высказывания:
а) «Треугольник является прямоугольным тогда и только тогда, когда имеет место с2=а2+в2»; б) «Число делится на 3 тогда и только тогда, когда сумма цифр в записи числа делится на 3». Запишите данные высказывания в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций.
Решение:
а) А: «Треугольник является прямоугольным» В: «с2=а2+в2»
АÛВ – данное высказывание АÛВº(АÞВ)Ù(ВÞА)
(АÞВ)Ù(ВÞА): «Если треугольник прямоугольный, то с2=а2+в2 и если с2=а2+в2, то треугольник является прямоугольным».
б) А: «Число делится на 3».
В: «Сумма цифр в записи числа делится на 3».
АÛВ º (АÞВ)Ù(ВÞА)
(АÞВ)Ù(ВÞА): «Если число делится на 3, то сумма цифр в записи числа делится на 3, и если сумма цифр в записи числа делится на 3, то число делится на 3».
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания IV уровня).
1. Составьте таблицу истинности (  Þ(УÙ
Þ(УÙ 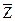 ))Þ((
))Þ((  ÚХ)Þ
ÚХ)Þ 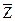 ).
).
2. Составьте таблицу истинности ((ХÙ 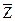 )ÞУ)Ù(
)ÞУ)Ù(  Þ(
Þ(  ÚZ)).
ÚZ)).
3. Составьте таблицу истинности (ХÞ(УÚ 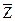 ))Þ((
))Þ((  ÙZ)Þ
ÙZ)Þ  ).
).
4. Составьте таблицу истинности 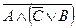

5. Составьте таблицу истинности 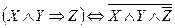
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания V уровня).
1. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) 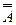 Û
Û  ; б)
; б)  Ú
Ú 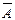 ; в)
; в) 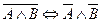
2. Докажите, что следующие высказывания являются тождествами (тавтологиями): а)  ; б) (
; б) ( 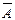 Þ
Þ  ) Þ
) Þ  ; в)
; в)  Ú
Ú 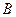 Û
Û 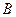 Ú
Ú  .
.
3. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) АÚАÛА; б) АÞВÛ  Þ
Þ 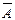 .
.
4. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) 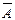 Þ(АÞВ); б) ((АÞВ)ÞА)ÛА.
Þ(АÞВ); б) ((АÞВ)ÞА)ÛА.
5. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) (АÛВ)Û(ВÛА); б) (АÞВ)Ú(ВÞА).
|
из
5.00
|
Обсуждение в статье: ТЕМА № 2. ЛОГИКА ВЫСКАЗЫВАНИЙ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

