 |
Главная |
C) асимптотика решений уравнения Бесселя, нули функции Бесселя
|
из
5.00
|
Функции Бесселя (любые решения уравнения Бесселя) имеют особенность в нуле. Решение уравнения Бесселя при  имеет следующий вид:
имеет следующий вид:  . Докажем это.
. Докажем это.
Для этого сделаем замену:  , подставим
, подставим  , первые производные ушли, осталось:
, первые производные ушли, осталось:  . Таким образом:
. Таким образом:  , будем искать
, будем искать 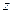 в виде:
в виде:  . Надо найти две функции:
. Надо найти две функции:  и
и  .
.
 положим
положим 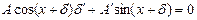 , получим
, получим  . Тогда
. Тогда  , подставим в уравнение:
, подставим в уравнение:  , т.о. получили систему:
, т.о. получили систему: 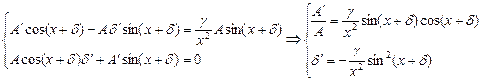 . Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
. Получили систему, разрешённую относительно производных, но не нелинейную. Оценим. Проинтегрируем и запишем для первого и второго уравнений:
 . При больших значениях
. При больших значениях  ,
,  и
и  имеют вид констант.
имеют вид констант.
Получим вид  :
:  и
и  :
:  .
.
Тогда  - общая формула для любой цилиндрической функции.
- общая формула для любой цилиндрической функции.
Асимптотики функций Бесселя и Неймана:


d) краевая задача на собственные значения:  , её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
, её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
Рассмотрим краевую задачу на собственные значения.  на отрезке
на отрезке 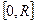 , или:
, или:  , отличается от уравнения Бесселя наличием параметра
, отличается от уравнения Бесселя наличием параметра  .
.
Первое решение: - тождественный ноль, а задача Штурма-Лиувилля – это задача на собственные функции и собственные значения - заключается в нахождении таких значений  , при которых существует нетривиальное решение.
, при которых существует нетривиальное решение.
Сделаем замену:  , (
, (  )
) 
 , его общее решение
, его общее решение  , константы находим из начального условия. Из ограниченности
, константы находим из начального условия. Из ограниченности  находим, что
находим, что  , из второго условия
, из второго условия  находим что:
находим что:  - это уравнение для определения
- это уравнение для определения  . У
. У  бесконечно много нулей:
бесконечно много нулей:  и
и 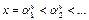 , тогда можно написать, что
, тогда можно написать, что  . Тогда собственные значения
. Тогда собственные значения  - их бесконечно много, и соответственно собственные функции
- их бесконечно много, и соответственно собственные функции 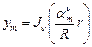 .
.
Все собственные значения действительны и положительны. Это следует из самосопряженности оператора 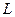 . Убедимся в его самосопряженности. Напишем формулу Грина
. Убедимся в его самосопряженности. Напишем формулу Грина
 ,
,  - т.е. оператор самосопряжённый. Это значит, что все собственные значения действительны и положительны, т.к.
- т.е. оператор самосопряжённый. Это значит, что все собственные значения действительны и положительны, т.к.  и
и 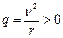 .
.
Все собственные функции, отвечающие разным собственным значениям ортогональны с весом 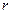 :
: 
Теорема Фурье-Бесселя (о полноте)
Любая функция  , которая на отрезке
, которая на отрезке 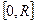 допускает дифференцирование и удовлетворяет граничным условиям:
допускает дифференцирование и удовлетворяет граничным условиям:  , разлагается в абсолютно и равномерно сходящийся ряд по функциям Бесселя:
, разлагается в абсолютно и равномерно сходящийся ряд по функциям Бесселя:  . Коэффициенты находятся интегрированием, т.к. это разложение по ортогональному базису.
. Коэффициенты находятся интегрированием, т.к. это разложение по ортогональному базису. 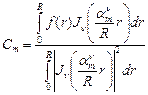 .
.
В задаче на собственные функции и собственные значения всё будет аналогично, если вместо краевого условие первого рода мы возьмём  , тогда
, тогда  - будут корнями уравнения:
- будут корнями уравнения:  .
.
e) модифицированное уравнение Бесселя, ограниченность решения  , свойства, общее решение, понятие о функции
, свойства, общее решение, понятие о функции 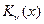 .
.
Рассмотрим уравнение:  , оно отличается знаком перед
, оно отличается знаком перед 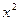 . Сделаем замену
. Сделаем замену  , тогда подставим и получим уравнение:
, тогда подставим и получим уравнение: 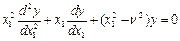 , получили уравнение Бесселя. Его ограниченное решение:
, получили уравнение Бесселя. Его ограниченное решение:  - модифицированная функция Бесселя.
- модифицированная функция Бесселя.
В качестве С возьмем  , тогда
, тогда  . Он отличается знакопостоянством. Рассмотрим его асимптотику:
. Он отличается знакопостоянством. Рассмотрим его асимптотику:  . Модифицированная функция заведомо не имеет нулей (только на мнимой оси), т.к. все слагаемые положительные. Напишем базис. Первая базисная функция -
. Модифицированная функция заведомо не имеет нулей (только на мнимой оси), т.к. все слагаемые положительные. Напишем базис. Первая базисная функция -  , вторая базисная функция -
, вторая базисная функция -  - функция Макдональда.
- функция Макдональда.  - действительна для действительных
- действительна для действительных  . Её асимптотика
. Её асимптотика  , тогда общее решение можно записать так:
, тогда общее решение можно записать так:  . Из линейной независимости
. Из линейной независимости  и
и  следует, что
следует, что  в точке
в точке 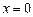 имеет полюс
имеет полюс  -го порядка.
-го порядка.
f) Сводная таблица.
| Лапласиан в цилиндрических координатах: | 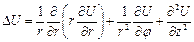
|
| Лапласиан в сферических координатах: | 
|
| Уравнение Бесселя: (уравнение для цилиндрических функций) | 
|
решение уравнения Бесселя при  (асимптотика): (асимптотика):
| 
|
| Функция Бесселя первого рода: |  ; ; 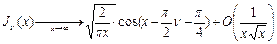
|
| Модифицированное уравнение Бесселя: | 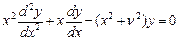
|
| Модифицированная функция Бесселя: |  ; ; 
|
| Функция Неймана: |  ; ; 
|
| Функции Ханкеля: |  ; ; 
|
| Функция Макдональда: |  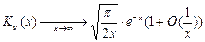
|
| рекуррентные соотношения: | 1)  2)
2)  
|
| функция Бесселя полуцелых порядков: |  ; ; 
|
| рассмотрим краевую задачу (задачу на собственные значения и собственные функции): | 
 , где , где 
|
| Ортогональность (и нормировка): | 
|
12. Краевая задача  с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора
с двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора  .
.
Рассмотрим уравнение: (*)  и пусть
и пусть 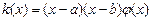 - имеет два ноля.
- имеет два ноля.

| Известно ограниченное решение в точке b, а также ограниченное решение в точке a. Возможен случай, когда решение в точке  перейдёт в ограниченное решение в точке перейдёт в ограниченное решение в точке 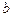 : :  . Но в общем случае всё множество решения, как правило, неограниченно. Исключительная ситуация может быть в случае нулевого решения. Таким образом возникает задача нахождения таких собственных значений λ, при которых задача - . Но в общем случае всё множество решения, как правило, неограниченно. Исключительная ситуация может быть в случае нулевого решения. Таким образом возникает задача нахождения таких собственных значений λ, при которых задача -  при при  - имеет нетривиальное решение; роль граничных условий здесь играет требование на ограниченность решения - имеет нетривиальное решение; роль граничных условий здесь играет требование на ограниченность решения 
|
Полученные функции, отвечающие различным собственным значениям, будут ортогональны, то есть оператор  должен быть самосопряжённым.
должен быть самосопряжённым.
Самосопряженность оператора 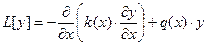
Используя 2-ую формулу Грина получаем: 
|
из
5.00
|
Обсуждение в статье: C) асимптотика решений уравнения Бесселя, нули функции Бесселя |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

