 |
Главная |
ТЕМА 6. КОМПЛЕКСНЫЕ ЧИСЛА
|
из
5.00
|
Комплексными называются числа вида z=x+iy, где x и y-действительные числа, а i2 =-1. Число x называется действительной частью комплексного числа z, а число y – коэффициент при i – мнимой частью. Число  =x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль
=x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль  комплексного числа z вычисляется по формуле
комплексного числа z вычисляется по формуле
 .
.
Угол  образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
Любое комплексное число z можно представить в алгебраической форме z = x + iy и в тригонометрической форме z= r (cosj +isinj). Здесь  , j=Аrgz -, причем различные значения аргумента
, j=Аrgz -, причем различные значения аргумента  отличаются на 2
отличаются на 2  k
k  , где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию -
, где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию -  <j<
<j<  . Таким образом Аrgz = аrgz+2
. Таким образом Аrgz = аrgz+2  к.
к.
Комплексные числа z еще можно представить в показательной форме z =rеij, где r и j - то, что и в тригонометрической форме.
 y
y
z
 |
r



 o
o  x
x
Рис.2
Пример
Найти корни уравнения  .
.
Решение. Находим модуль и аргумент числа 


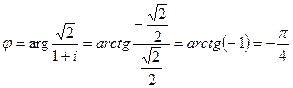 .
.
Тогда корни данного уравнения определяем по формулам
 , к = 0,1,2, т.е. уравнение имеет три корня:
, к = 0,1,2, т.е. уравнение имеет три корня:
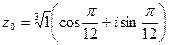 , при к=0;
, при к=0;
 , при к=1;
, при к=1;
 , при к=2
, при к=2
или 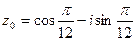
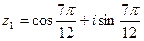

КОНТРОЛЬНАЯ РАБОТА № 1
Задание 1. Решить систему уравнений методом Гаусса и с помощью обратной матрицы
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
6. 
17. 
18. 
19. 
20. 
21. 

22. 
23. 
28. 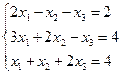
24. 
25. 
26. 
27. 

 29.
29. 

30. 

Задание 2.
В задачах 1-30 даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X"=  через X=
через X= 
1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 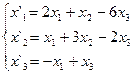

11. 

12. 

13. 
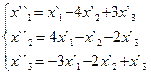
14. 

15. 

16. 

17. 

18. 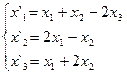
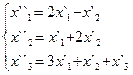
19. 

20. 

21. 

22. 

23. 

24. 

25. 

26. 
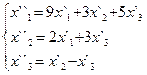
27. 

28. 

29. 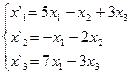

30. 

Задание 3.
Найти собственные векторы и собственные значения линейного преобразования, заданного в некотором базисе матрицей.
1.  2.
2.  3.
3. 
4.  5.
5.  6.
6. 
7.  8.
8.  9.
9. 
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15. 
16.  17.
17.  A=
A=  18.
18. 
19.  20.
20.  21.
21. 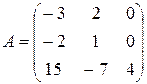
22. 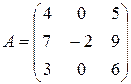 23.
23.  24.
24. 
25.  26.
26.  27.
27. 
28.  29.
29. 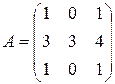 30.
30. 
Задание 4.
Дано комплексное число  :
:
1) Записать число  в алгебраической и тригонометрической формах.
в алгебраической и тригонометрической формах.
2) Найти и изобразить на плоскости все корни уравнения Z3 +  = 0.
= 0.
1.  2.
2.  3.
3.  4.
4. 
5.  6.
6.  7.
7.  8.
8. 
9.  10.
10.  11.
11.  12.
12. 
13.  14.
14.  15.
15.  16.
16. 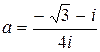
17.  18.
18.  19.
19.  20.
20. 
21.  22.
22.  23.
23.  24.
24. 
25.  26.
26.  27.
27.  28.
28. 
29.  30.
30. 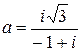
ТЕМА 8. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
Не повторяя данных в учебнике определений и доказательств, рассмотрим ряд конкретных примеров, в которых отражена сущность теории пределов.
Пример 1.
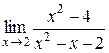

Подстановка на место x его предельного значения, т.е. числа 2, приводит к неопределенности вида  . Преобразуем дробь
. Преобразуем дробь  до перехода к пределу, разложив числитель и знаменатель на множители
до перехода к пределу, разложив числитель и знаменатель на множители


теперь имеем  .
.
Пример 2.
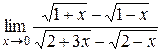
Подстановка предельного значения x ( т.е. числа 0) приводит к неопределенности вида  . Преобразуем дробь под знаком предела до того как
. Преобразуем дробь под знаком предела до того как  .
.

| |
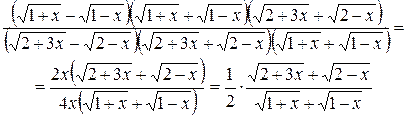
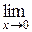
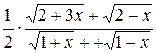 =
=  .
.
Пример 3.
Найти  .
.
Здесь выражение под знаком пределов представляет собой отношение двух многочленов аргумента n. И числитель и знаменатель дроби стремятся к бесконечности. В этом случае говорят, что имеется «неопределенность типа  ».
».
Для отыскания предела следует раскрыть скобки и разделить числитель и знаменатель на высшую степень.
Получаем

Так как 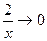 при
при  .
.
Пример 4.
Найти  .
.
Как и в примере 3 целесообразно числитель и знаменатель дроби разделить на старшую степень, которую легко увидеть, если под каждым корнем оставить лишь старшую степень n (остальные слагаемые играют малую роль при  ).
).
В данном примере получаем  .
.
Значит старшая степень -x. Разделив числитель и знаменатель на x, будем иметь  , так как
, так как 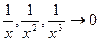 при x
при x 
Пример 5.
Найти  .
.
Здесь мы имеем «неопределенность типа (  )».
)».
Умножив и разделив эту разность на сопряженное выражение 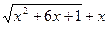 , получим
, получим 
.
Такой предел рассматривался в предыдущем примере. Разделив числитель и знаменатель на x, будем иметь  .
.

Пример 6.
Вычислить 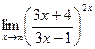
Здесь основание степени  при x
при x  ,а показатель
,а показатель  ; таким образом имеем «неопределенность типа
; таким образом имеем «неопределенность типа 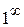 ». В этом случае следует воспользоваться вторым замечательным пределом:
». В этом случае следует воспользоваться вторым замечательным пределом: 

 .
.
Преобразовав выражение, получаем
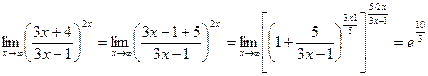 ,
,
так как выражение в квадратных скобках стремится к е, а  при
при  .
.
Пусть, например, требуется вычислить  .
.
Рассмотрим случай 
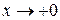 , тогда показатель стремится к
, тогда показатель стремится к  , основание к 4, значит искомый предел равен
, основание к 4, значит искомый предел равен  . Если
. Если  , то показатель
, то показатель 
 ,основание стремится к 4 и искомый предел равен 0. Итак
,основание стремится к 4 и искомый предел равен 0. Итак
 .
. 
Пример 7.
Найти  .
.
Для решения применим предел 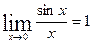
Здесь при  и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа
и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа  ». Используя формулу тригонометрии
». Используя формулу тригонометрии
имеем

Заметим, что cos(15x)  при x
при x  , поэтому
, поэтому

Пример 8.
Найти  .
.
Известно ( следствие теоремы Безу), что если многочлен обращается в нуль при  , то он делится без остатка на
, то он делится без остатка на  , поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа
, поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа  », то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1
», то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1


получаем
 .
.
Пример 9.
Найти точки разрыва функции  . Изобразить график в окрестности точки разрыва.
. Изобразить график в окрестности точки разрыва.
Знаменатель  , при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.
, при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.

При тех же рассуждениях получим  .
. 
Итак, пределы функции слева и справа при  равны, но в точке x=1 функция не определена, значит, точка устранимого разрыва. График функции в окрестности точки разрыва выглядит следующим образом:
равны, но в точке x=1 функция не определена, значит, точка устранимого разрыва. График функции в окрестности точки разрыва выглядит следующим образом:
 |
Такой разрыв называют устранимым разрывом, так как доопределив функцию f(x) надлежащим образом (положив при x=1 f(x) =4) получим непрерывную функцию:
 .
.
 ТЕМА 9. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
ТЕМА 9. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
При освоении техники дифференцирования необходимо заучить таблицу производных основных элементарных функций и научиться пользоваться основными правилами дифференцирования. При этом особое внимание следует уделить дифференцированию сложных функций.
Пример.1
 .
.
Данную функцию можно представить в виде цепочки двух простых функций:  ;
;  .Согласно правилу дифференцирования сложной функции имеем:
.Согласно правилу дифференцирования сложной функции имеем:  .
.
Но 
 , а потому
, а потому 
 .
.
Пример 2.
 .
.
Очевидно, что 
 и тогда
и тогда  ,так как
,так как  , то
, то  .
.
В двух рассмотренных примерах каждая из сложных функций содержала лишь один промежуточный аргумент u и поэтому разлагалась на цепочку из двух простых функций. В более сложных случаях промежуточных аргументов может оказаться больше одного.
ИССЛЕДОВАНИЕ ФУНКЦИЙ
В дополнение к примерам, разобранным в тексте учебника, рассмотрим еще следующий пример.
Пример. Исследовать функцию  и построить ее график.
и построить ее график.
1. Область определения данной функции - вся числовая ось, кроме точки 
2. Функция не является ни четной, ни нечетной. Действительно, f(-x)=  и
и 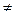 -f(x).
-f(x).
3. Прямая  есть вертикальная асимптота, так как точка
есть вертикальная асимптота, так как точка  есть точка разрыва второго рода.
есть точка разрыва второго рода.
4.Найдем угловой коэффициент наклонной асимптоты, предполагая, что такая существует:  ;
; 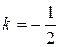 .
.
Находим свободный член b для уравнения асимптоты: 
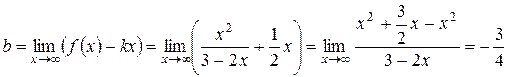 .
.
Итак, уравнение асимптоты:  .
.
5. Находим критические точки, т.е. точки, в которых первая производная обращается в нуль:  .
.
Производная обращается в нуль, если  ,
,  и
и  .
.
Подвергая испытанию каждую из этих двух точек, можно узнать, меняется ли знак производной при прохождении аргумента через точки 0 и 3:
а) y¢<0 при x<0 ( функция убывает), y¢>0 при x>0 ¢ ( функция yвозрастает), следовательно, в точке x=0 функция y достигает минимума, причем  ;
;
б) при x<3 y¢>0 (возрастает); x>3 y¢<0 (убывает).
Таким образом, в точке x=3 функция достигает максимума, равного  .
.
6. Для уточнения графика функции найдем точки перегиба и установим направление вогнутости ( выпуклости) кривой в различных интервалах, для чего обращаемся ко второй производной). Положительный множитель 2, входящий в первую производную, может быть отброшен, поскольку он не влияет на знак второй производной. Имеем

Если  , то y²>0 и кривая обращена вогнутостью вверх.
, то y²>0 и кривая обращена вогнутостью вверх.
При  знаменатель ( 3- 2х)3 <0 и
знаменатель ( 3- 2х)3 <0 и  .
.
Следовательно, справа от точки разрыва кривая обращена вогнутостью вниз. Точек перегиба нет, y² ни при каком значении из области определения не обращается в нуль. Принимая во внимание выводы всех предыдущих пунктов, строим график функции
 |
|
из
5.00
|
Обсуждение в статье: ТЕМА 6. КОМПЛЕКСНЫЕ ЧИСЛА |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

