 |
Главная |
Сделать проверку решения. Вариант СЛАУ Вариант СЛАУ
|
из
5.00
|
| Вариант | СЛАУ | Вариант | СЛАУ |
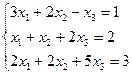
| 
| ||
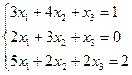
| 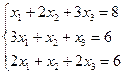
| ||

| 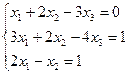
| ||
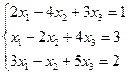
| 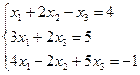
| ||

| 
|
Задание 5
Найти общее и частное решение неоднородной СЛАУ. Сделать проверку решения.

Решение:
Количество уравнений в системе равно 4, а количество переменных в системе 5, следовательно, т.к.  - система имеет бесконечное множество решений или не имеет решений.
- система имеет бесконечное множество решений или не имеет решений.
Для решения системы выпишем расширенную матрицу системы:
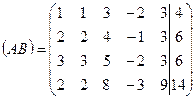 .
.
Приведем расширенную матрицу системы к эквивалентной матрице системы в ступенчатом виде.

|
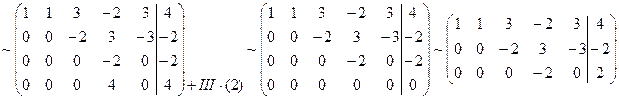
 - по теореме Кронекера-Капелли система имеет решение, если ранг расширенной матрицы равен рангу приведенной матрицы.
- по теореме Кронекера-Капелли система имеет решение, если ранг расширенной матрицы равен рангу приведенной матрицы.

Выразим базисные переменные через свободные

|

Запишем частное решение, придавая любые значения свободным переменным.
Например, при 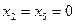 значение
значение  , а
, а 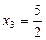 .
.
Ответ в виде вектора: 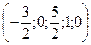 .
.
Сделаем проверку, подставив найденное решение в каждое уравнение системы.
Проверка:
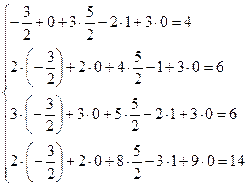 ;
; 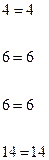 .
.
Итак, мы видим, что после подстановки в систему каждое уравнение обратилось в числовое тождество. Следовательно, решение системы найдено верно.
Варианты задания 5
Найти общее и частное решение неоднородной СЛАУ. Сделать проверку решения. (метод Гаусса)
| Вариант | СЛАУ | Вариант | СЛАУ |
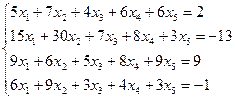
| 
| ||
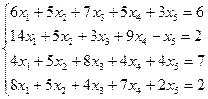
| 
| ||
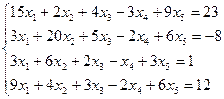
| 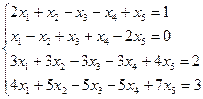
| ||

| 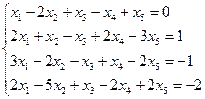
| ||

| 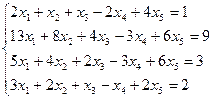
|
Задание 6
Найти фундаментальный набор решений однородной СЛАУ. Сделать проверку решения.

Решение:
Количество уравнений в системе равно 4, а количество переменных в системе 5, следовательно, т.к.  - система имеет бесконечное множество решений.
- система имеет бесконечное множество решений.
Для решения системы выпишем исходную матрицу системы:
 .
.
Приведем исходную матрицу системы к эквивалентной матрице системы в ступенчатом виде.

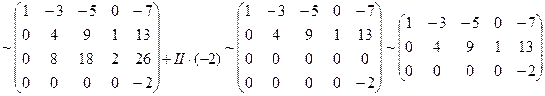
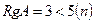 - система имеет бесконечное множество решений, включая нулевое - тривиальное.
- система имеет бесконечное множество решений, включая нулевое - тривиальное.
|
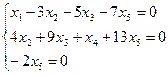
Выразим базисные переменные через свободные



Найдем фундаментальный набор решений.
Количество фундаментальных решений равно количеству свободных слагаемых, т.е. 2.
Придадим свободным переменным любые такие значения, которые образуют квадратную матрицу с определителем не равным нулю; самый простой набор таких значений – единичная матрица.
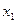
| 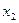
| 
| 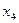
|  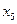
|
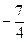
| 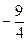
| |||

| 
|

Запишем ответ в виде двух векторов:
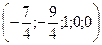 и
и  .
.
Сделаем проверку, подставив найденное решение в каждое уравнение системы.
Проверка:
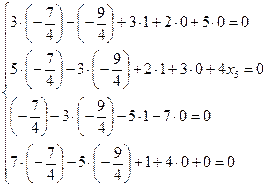 ;
;  .
.
 ;
;  .
.
Итак, мы видим, что после подстановки в систему каждое уравнение обратилось в числовое тождество. Следовательно, решение системы найдено верно.
Варианты задания 6
|
из
5.00
|
Обсуждение в статье: Сделать проверку решения. Вариант СЛАУ Вариант СЛАУ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


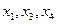 - базисные,
- базисные, 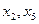 - свободные
- свободные
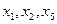 - базисные,
- базисные,  - свободные
- свободные