Методы анализа графа. Поиск в ширину. Нахождение кратчайших путей в графе

Вход алгоритма: граф 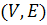и фиксированная вершина .

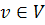Выход алгоритма: компонента связности графа, в которую входит вершина .

Описание алгоритма: на этапах алгоритма строится последовательность расширяющихся множеств вершин

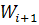по следующему рекуррентному принципу: – исходная фиксированная вершина . Пусть построены множества . Тогда множество включает вершины множества , а также вершины, которые смежны с вершинами :

Таким образом, – сама вершина . – те вершины, которые достижимы из начальной вершины не более чем за один шаг. – те вершины, которые достижимы из начальной вершины не более чем за два шага… Место для формулы.

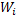
Как только два соседних множества совпадут, алгоритм завершает свою работу.

Пусть начальная вершина – 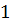. Тогда:

Поиск в ширину позволяет находить длины кратчайших путей и сами пути. Из фиксированной вершины во все вершины графа (для простоты считаем, что граф связан).

Определение. Кратчайший путь между вершиной и 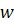– это путь, соединяющий данные вершины и содержащий наименьшее число ребер.

Утверждение. Вершины, впервые помеченные на k-ом этапе алгоритма поиска в ширину есть те вершины графа, кратчайший путь от которых до начальной вершины равен .

Доказательство:

Проведем доказательство методом индукции по номеру этапа алгоритма.

Для начального нулевого этапа утверждение очевидно. Начальная вершина множества и кратчайший путь от вершины до нее равен .

Пусть утверждение справедливо для k-ого этапа алгоритма. Докажем справедливость утверждения для 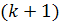-ого этапа. Так как по построению алгоритма на 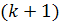этапе вновь помеченные вершины есть вершины, которые смежны с вершинами, помеченными на предыдущем k-ом этапе, то из данных вершин обязательно найдется путь в вершину , содержащий не более чем 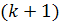ребро.

Более короткого пути, чем из k+1-ого ребра в вновь помеченные вершины на k+1 этапе бытьть не может. В последнем случае эти вершины были бы отмечены на более раннем этапе (по предположению индукции).

Утверждение доказано.

Рассмотрим более общую задачу поиска кратчайшего пути в графе, в котором каждому ребру предписано положительное число – его длина (расстояние между соответствующей парой вершин). Считаем, что это число положительное целое.

Таким образом, на вход алгоритма подается сеть 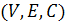и начальная вершина , где 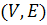– неориентированный связный граф, а 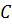– положительная целочисленная (стоимостная) функция длины, заданная на ребрах графа.

На выходе алгоритма должны быть получены значения кратчайших путей из вершины в любую другую вершину графа 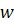. Если вершина 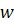не связана с вершиной , считаем, что расстояние равно .

Сведем рассматриваемую задачу к предыдущей задаче поиска кратчайших путей для графа, в котором функция длины единичная. Для этого совершим следующее преобразование:

Рассмотрим произвольное ребро в заданном графе. Длина данного ребра равна .

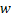
В данное ребро добавим вершину, а длину каждого полученного ребра будем считать равной .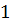

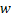
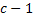
Данное преобразование применим к каждому ребру графа. При этом длины кратчайших путей между вершинами исходного графа не изменятся, а функция длины в полученном графе единичная. Исходя из этого, можно применить алгоритм поиска в ширину для полученного графа.

Примечание.Данный алгоритм будет неэффективным в силу того, что числа в компонентах связности хранятся в двоичной системе исчисления, поэтому целое число длины будет требовать лишь битов памяти. Преобразованный граф будет требовать экспоненциальную память, по сравнению с памятью первоначального графа, т.к. ребро длины преобразуется в ребер. Если в первоначальной задаче для записи числа требуется бит, то в полученной задаче будет необходимо бит для хранения новых вершин в графе.