 |
Главная |
Поиск в глубину. Нахождение остовного дерева с помощью поиска в глубину
|
из
5.00
|
Вход алгоритма: неориентированный граф 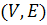 и фиксированная вершина
и фиксированная вершина 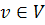 .
.
Выход алгоритма: компонента связности графа, в которую входит вершина  .
.
Описание алгоритма: алгоритм передвигается по ребрам графа, оставляя пометки в вершинах графа. Начальную вершину пометим номером этой же вершины 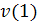 . Рекурсивный шаг алгоритма описывается следующим образом: Есть текущая вершина
. Рекурсивный шаг алгоритма описывается следующим образом: Есть текущая вершина  . Рассмотрим вершины графа, смежные с текущей. Если среди этих вершин найдется вершина без пометки (обозначим ее
. Рассмотрим вершины графа, смежные с текущей. Если среди этих вершин найдется вершина без пометки (обозначим ее 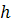 ), то передвигаемся в вершину
), то передвигаемся в вершину 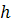 и помечаем ее предыдущей вершиной
и помечаем ее предыдущей вершиной  .
.
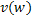
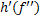
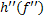
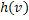
Если все вершины, смежные с вершиной  помечены, то переходим обратно в вершину
помечены, то переходим обратно в вершину 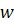 , которой была помечена текущая вершина
, которой была помечена текущая вершина  . Алгоритм заканчивает свою работу тогда, когда текущей вершиной является начальная, а все смежные с ней вершины помечены.
. Алгоритм заканчивает свою работу тогда, когда текущей вершиной является начальная, а все смежные с ней вершины помечены.
Пример. Рассмотрим граф:
| 1(1) |
| 2(4) |
| 4(7) |
| 7(6) |
| 8(7) |
| 3(1) |
| 5(3) |
| 6(5) |
Начальная вершина 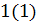 . Выбираем смежные вершины:
. Выбираем смежные вершины: 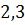 . Они непомечены. Двигаемся в любую из непомеченных вершин.
. Они непомечены. Двигаемся в любую из непомеченных вершин.
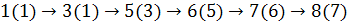
Возвращаемся обратно до тех пор, пока у текущей вершины есть непомеченные смежные с ней вершины.
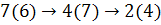
Возвращаемся обратно.
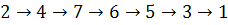
Помеченные вершины - компонента связности.
Покажем корректность данного алгоритма.
Покажем, что отмеченные вершины есть компонента связности, в которой находится исходная вершина  .
.
Пусть вершина 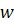 была отмечена на некотором шаге алгоритма. Следовательно, эта вершина связана с исходной вершиной
была отмечена на некотором шаге алгоритма. Следовательно, эта вершина связана с исходной вершиной  , т.к. по построению алгоритма движение происходило непрерывно по ребрам графа, и путь до исходной вершины
, т.к. по построению алгоритма движение происходило непрерывно по ребрам графа, и путь до исходной вершины  из
из 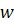 можно получить, двигаясь в обратном направлении по меткам вершин. Наоборот, существует вершина
можно получить, двигаясь в обратном направлении по меткам вершин. Наоборот, существует вершина 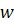 , связанная с вершиной
, связанная с вершиной  . Покажем, что она будет помечена на некотором шаге алгоритма.
. Покажем, что она будет помечена на некотором шаге алгоритма.
Предположим противное: вершина 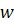 не была помечена алгоритмом. Рассмотрим первую вершину на пути из начальной вершины
не была помечена алгоритмом. Рассмотрим первую вершину на пути из начальной вершины  в вершину
в вершину 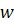 , которая не была помечена. Пусть это будет вершина
, которая не была помечена. Пусть это будет вершина 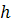 . Вершину
. Вершину 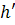 и все вершины между
и все вершины между  и
и 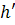 помечены.
помечены.
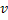
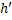
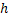
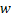
Рассмотрим последний шаг алгоритма, когда текущая вершина была 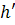 . Тогда в очередной момент времени обязательно будет рассмотрена вершина, из которой была помечена вершина
. Тогда в очередной момент времени обязательно будет рассмотрена вершина, из которой была помечена вершина 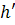 , т.е. происходило обратное движение при непомеченной смежной вершине.
, т.е. происходило обратное движение при непомеченной смежной вершине.
Это противоречит построению алгоритма. Что и требовалось доказать.
Свойство алгоритма поиска в глубину.
Рассмотрим граф 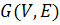 – исходный граф. Будем считать его связным.
– исходный граф. Будем считать его связным. 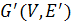 будем обозначать граф с тем же множеством вершин
будем обозначать граф с тем же множеством вершин 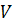 и множеством ребер
и множеством ребер 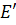 (это ребра, по которым происходит движение алгоритма поиска в глубину хотя бы один раз). Тогда справедливо свойство:
(это ребра, по которым происходит движение алгоритма поиска в глубину хотя бы один раз). Тогда справедливо свойство:
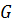 – граф без циклов
– граф без циклов
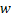
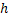
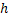

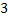
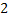
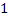
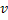
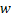
Рассмотрим произвольное ребро 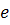
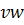 , по которому движение происходит хотя бы один раз, следовательно, либо вершина
, по которому движение происходит хотя бы один раз, следовательно, либо вершина  будет иметь метку
будет иметь метку 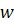 , либо наоборот. Действительно, рассмотрим один момент, когда алгоритм проходил по ребру
, либо наоборот. Действительно, рассмотрим один момент, когда алгоритм проходил по ребру 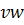 . Если это движение было из
. Если это движение было из  в
в 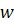 , тогда вершина
, тогда вершина 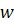 получила метку
получила метку  , либо наоборот – движение было из
, либо наоборот – движение было из 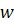 в
в  , а вершина
, а вершина  получила метку
получила метку 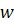 .
.
Предположим противное. 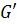 содержит некоторый цикл. Пусть
содержит некоторый цикл. Пусть 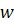 – первая вершина цикла, которую посетил алгоритм. Это значит, что метка вершины
– первая вершина цикла, которую посетил алгоритм. Это значит, что метка вершины 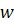 будет отлична от всех остальных вершин цикла. Тогда последовательно перебираем вершины цикла. Тогда, вершина
будет отлична от всех остальных вершин цикла. Тогда последовательно перебираем вершины цикла. Тогда, вершина 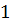 должна иметь метку
должна иметь метку 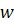 , вершина
, вершина 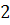 метку
метку 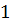 и т.д. Рассмотрим последнюю вершину
и т.д. Рассмотрим последнюю вершину 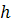 в цикле. Она будет иметь метку предыдущей вершины
в цикле. Она будет иметь метку предыдущей вершины 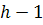 . Следовательно, для каждой вершины ребра
. Следовательно, для каждой вершины ребра 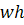 имеем противоречие с предложением выше. Метка каждой вершины
имеем противоречие с предложением выше. Метка каждой вершины 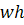 отлична от
отлична от 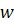 и от
и от 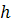 , хотя по этому ребру проходило движение алгоритма.
, хотя по этому ребру проходило движение алгоритма.
Определение. Деревом называется связный граф без циклов.
Пример. Простая цепь есть дерево:
Утверждение. Минимальное число ребер в графе на 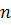 вершинах (
вершинах ( 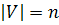 ), которые обеспечивают связность графа равно
), которые обеспечивают связность графа равно 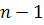 .
.
Доказательство
1. Очевидно, что 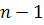 ребро достаточно, чтобы связать
ребро достаточно, чтобы связать 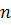 вершин. такое соединение есть цепь из последовательных
вершин. такое соединение есть цепь из последовательных 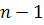 ребра. Покажем, что меньшим числом ребер обойтись невозможно. Покажем это математической индукцией по числу вершин в графе. Для двух вершин в графе это очевидно. С двумя вершинами без ребер граф связным не является.
ребра. Покажем, что меньшим числом ребер обойтись невозможно. Покажем это математической индукцией по числу вершин в графе. Для двух вершин в графе это очевидно. С двумя вершинами без ребер граф связным не является.
Допустим, утверждение доказано для 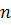 вершин, т.е. минимальное число ребер для связности
вершин, т.е. минимальное число ребер для связности 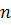 вершин будет равно
вершин будет равно 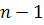 . Рассмотрим
. Рассмотрим 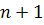 вершину и предположим противное, что для
вершину и предположим противное, что для 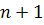 вершины можно обойтись
вершины можно обойтись 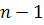 ребром, чтобы их связать. Рассмотрим соответствующий граф
ребром, чтобы их связать. Рассмотрим соответствующий граф 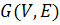 ,
, 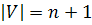 ,
, 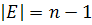 . Этот граф не имеет циклов (в противном случае можно удалить любое ребро из цикла и граф останется связным – любые две вершины соединены двумя не пересекающимися путями, следовательно, если граф содержит цикл, то можно было бы уменьшить число ребер, которые связывают вершины этого графа). Теперь покажем, что в связном графе без цикла обязательно существует висячая вершина (имеющая только одну смежную с ней вершину). Предположим противное – граф без циклов висячих вершин не имеет, т.е. каждая вершина смежна по крайней мере с двумя другими. Рассмотрим движение по ребрам графа. Из текущей вершины v передвигаемся в вершину отличную от той, из которой мы попали в v (так как число смежных вершин не менее двух, такое движение возможно
. Этот граф не имеет циклов (в противном случае можно удалить любое ребро из цикла и граф останется связным – любые две вершины соединены двумя не пересекающимися путями, следовательно, если граф содержит цикл, то можно было бы уменьшить число ребер, которые связывают вершины этого графа). Теперь покажем, что в связном графе без цикла обязательно существует висячая вершина (имеющая только одну смежную с ней вершину). Предположим противное – граф без циклов висячих вершин не имеет, т.е. каждая вершина смежна по крайней мере с двумя другими. Рассмотрим движение по ребрам графа. Из текущей вершины v передвигаемся в вершину отличную от той, из которой мы попали в v (так как число смежных вершин не менее двух, такое движение возможно
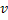
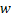
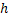
Как только попадем в вершину, где были ранее, остановимся. Не трудно видеть, что такая ситуация неизбежна в силу конечности числа вершин. В результате получим простой цикл 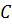 – противоречие исходному графу.
– противоречие исходному графу.
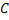
|
|
|
|
|
|
Таким образом, рассмотренный граф обязательно содержит висячую вершину 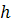 . Удалим вершину
. Удалим вершину 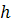 вместе с ребром, инцидентным ей. Очевидно, в результате получается связный граф с числом ребер
вместе с ребром, инцидентным ей. Очевидно, в результате получается связный граф с числом ребер 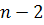 на
на 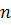 вершинах, что противоречит предположению индукции (для связности
вершинах, что противоречит предположению индукции (для связности 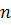 вершин необходимо
вершин необходимо 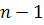 ребро).
ребро).
Рассмотрим граф 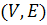 с числом вершин
с числом вершин 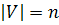 . Рассмотрим следующие 3 свойства графа:
. Рассмотрим следующие 3 свойства графа:
1) Связность
2) Отсутствие циклов
3) Число ребер в графе 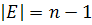 (далее будем рассматривать графы без петель).
(далее будем рассматривать графы без петель).
Утверждение. Любые два свойства из указанных порождают третье.
Доказательство:
(a) 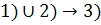
Покажем, что связный граф на 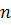 вершинах, не имеющий циклов, содержит
вершинах, не имеющий циклов, содержит 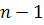 ребро. То есть, любое дерево на
ребро. То есть, любое дерево на 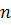 вершинах имеет
вершинах имеет 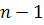 ребро. Доказательство будем проводить по индукции по числу вершин в дереве.
ребро. Доказательство будем проводить по индукции по числу вершин в дереве.
Дерево с единственной вершиной не имеет ребер. Допустим, что доказано, что любое дерево на 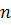 вершинах имеет
вершинах имеет 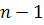 ребро. Рассмотрим дерево на
ребро. Рассмотрим дерево на 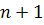 вершине. Как было замечено раньше, в любом дереве есть висячая вершина, т.е. вершина, которой инцидентно не более чем одно ребро. Удалим висячую вершину вместе с инцидентным ребром из дерева
вершине. Как было замечено раньше, в любом дереве есть висячая вершина, т.е. вершина, которой инцидентно не более чем одно ребро. Удалим висячую вершину вместе с инцидентным ребром из дерева 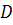 . В результате получим граф
. В результате получим граф 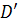 , который является связным и без циклов. По предположению индукции, число ребер в этом графе равно
, который является связным и без циклов. По предположению индукции, число ребер в этом графе равно 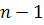 . Поэтому, в первоначальном дереве
. Поэтому, в первоначальном дереве 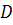 число ребер равно
число ребер равно 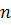 .
.
Что и требовалось доказать.
(b) 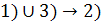
Покажем, что связный граф на 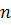 вершинах, содержащий
вершинах, содержащий 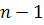 ребро не имеет циклов.
ребро не имеет циклов.
Предположим противное: рассматриваемый граф содержит цикл 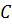 . Удалим какое-либо ребро
. Удалим какое-либо ребро 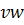 из данного цикла. При этом связность графа не нарушится, т.к. любая пара вершин в цикле графа соединена не пересекающимися путями в цикле. Поэтому полученный граф будет связным, имеющим то же число вершин
из данного цикла. При этом связность графа не нарушится, т.к. любая пара вершин в цикле графа соединена не пересекающимися путями в цикле. Поэтому полученный граф будет связным, имеющим то же число вершин 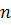 , и
, и 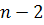 ребра. Получаем противоречие с тем, что минимальное число ребер для связности графа на
ребра. Получаем противоречие с тем, что минимальное число ребер для связности графа на 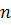 вершинах равно
вершинах равно 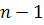 .
.
Что и требовалось доказать.
(c) 2 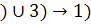
Покажем, что граф на 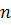 вершинах и
вершинах и 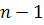 ребре, в котором отсутствуют циклы, является связным.
ребре, в котором отсутствуют циклы, является связным.
Предположим противное: рассматриваемый граф не является связным. Рассмотрим компоненты связности графа 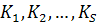 с числом вершин
с числом вершин 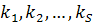 в компонентах связности соответственно. Компоненты связности являются деревьями, т.к. это связные графы без циклов. Поэтому, по доказанному, компоненты связности имеют соответственно
в компонентах связности соответственно. Компоненты связности являются деревьями, т.к. это связные графы без циклов. Поэтому, по доказанному, компоненты связности имеют соответственно 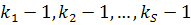 ребро. Тогда общее число ребер в таком графе равно
ребро. Тогда общее число ребер в таком графе равно
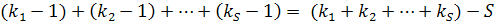
Так как граф не связный, то число компонент связности равно, по крайней мере, двум, то есть, 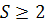 . Поэтому число ребер
. Поэтому число ребер 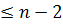 , что противоречит третьему свойству нашего графа: число ребер в нем равно
, что противоречит третьему свойству нашего графа: число ребер в нем равно 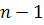 .
.
Что и требовалось доказать.
Таким образом, любые два из перечисленных трех свойств можно взять за основу определения дерева.
Рассмотрим граф 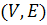 .
.
Определение. Подграфом графа 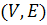 называется граф
называется граф 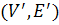 , где
, где 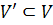 , а
, а 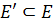 . Причем каждое ребро из подмножества
. Причем каждое ребро из подмножества 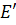 имеет оба конца в множестве
имеет оба конца в множестве 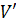 .
.
Определение. Пусть граф 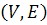 связный. Тогда остовным деревом графа
связный. Тогда остовным деревом графа 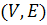 называется подграф графа
называется подграф графа 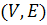 на том же самом множестве вершин
на том же самом множестве вершин 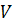 , который является деревом.
, который является деревом.
Пример. Рассмотрим граф на множестве, состоящем из 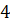 вершин. Остовным графом этого графа является граф, представленный справа:
вершин. Остовным графом этого графа является граф, представленный справа:
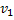
|
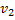
|
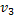
|
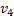
|
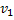
|
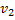
|
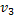
|
|
Утверждение. Любой связный граф имеет остовное дерево.
Доказательство:
Остов связного графа можно получить поиском в глубину, а именно, рассматривая все ребра 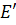 , которые были пройдены алгоритмом поиска в глубину. Все такие ребра содержат все вершины графа, и данное множество ребер не содержит циклов. Также остовное дерево связного графа можно получить последовательно удаляя ребра из имеющихся в графе циклов до тех пор, пока не получится граф без циклов.
, которые были пройдены алгоритмом поиска в глубину. Все такие ребра содержат все вершины графа, и данное множество ребер не содержит циклов. Также остовное дерево связного графа можно получить последовательно удаляя ребра из имеющихся в графе циклов до тех пор, пока не получится граф без циклов.
Укладки графов. Планарные графы.
Определение. Граф 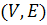 называется планарным, если его можно уложить на плоскости без пересечения ребер.
называется планарным, если его можно уложить на плоскости без пересечения ребер.
Пример. Полный граф (граф, содержащий всевозможные ребра) на 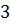 и
и 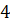 вершинах является планарным (
вершинах является планарным ( 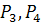 ):
):
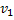
|
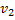
|
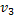
|
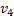
|
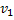
|
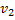
|
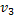
|
Примеры непланарных графов:
полный граф на 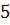 вершинах (
вершинах ( 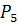 ) является непланарным;
) является непланарным;
двудольный граф с 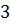 вершинами в каждой доле (
вершинами в каждой доле ( 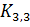 ) является непланарным.
) является непланарным.
Определение. Двудольным графом 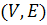 называется граф, вершины которого можно разбить на два непересекающегося множества
называется граф, вершины которого можно разбить на два непересекающегося множества 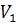 и
и 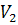 , любое ребро которого соединяет пару вершин из различных множеств
, любое ребро которого соединяет пару вершин из различных множеств 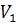 и
и 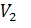 .
.
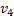
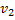
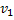
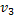
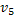
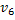
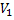
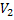
Определение. Полным двудольным графом называется двудольный граф, содержащий всевозможные ребра, концы которых расположены в разных долях 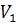 и
и 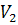 графа.
графа.
Покажем непланарность графов 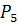 и
и 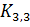 .
.
Предположим противное: граф 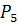 планарен. Рассмотрим укладку этого графа на плоскости без пересечений ребер. Рассмотрим цикл из
планарен. Рассмотрим укладку этого графа на плоскости без пересечений ребер. Рассмотрим цикл из 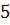 ребер, который соединяет рассмотренные вершины. Этот цикл разобьет плоскость на две связные области
ребер, который соединяет рассмотренные вершины. Этот цикл разобьет плоскость на две связные области 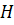 и
и 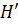 (любую пару вершин из одной и той же области можно соединить непрерывной линией, которая не пересекает ребра цикла, а пару вершин из различных областей связности соединить непрерывной линией без пересечений ребер нельзя). Рассмотрим ребро укладки, которое соединяет пару вершин
(любую пару вершин из одной и той же области можно соединить непрерывной линией, которая не пересекает ребра цикла, а пару вершин из различных областей связности соединить непрерывной линией без пересечений ребер нельзя). Рассмотрим ребро укладки, которое соединяет пару вершин 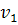 и
и 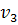 .
.
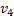
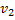
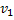
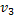
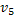
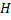
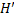
Это ребро будет расположено либо в области 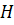 , либо в области
, либо в области 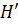 . Эти возможности подобны. Предположим, это ребро расположено в области
. Эти возможности подобны. Предположим, это ребро расположено в области 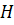 . Тогда пара вершин
. Тогда пара вершин 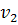 ,
, 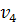 должна быть соединена ребром, расположенном в области
должна быть соединена ребром, расположенном в области 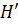 . Другая пара вершин –
. Другая пара вершин – 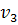 ,
, 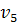 должна быть соединена ребром, расположенном в области
должна быть соединена ребром, расположенном в области 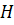 . Пара вершин
. Пара вершин 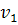 ,
, 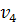 должна соединяться ребром из области
должна соединяться ребром из области 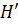 . Тогда пару вершин
. Тогда пару вершин 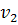 ,
, 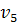 нельзя соединить ребром, не пересекающим другие ребра укладки.
нельзя соединить ребром, не пересекающим другие ребра укладки.
Покажем непланарность графа 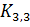 .
.
Такой граф содержит цикл, состоящий из 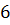 ребер. Доказательство будем строить от противного. Предположим, что существует планарная укладка графа
ребер. Доказательство будем строить от противного. Предположим, что существует планарная укладка графа 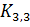 на плоскости. Тогда цикл из
на плоскости. Тогда цикл из 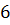 ребер разбивает плоскость на две области связности:
ребер разбивает плоскость на две области связности: 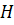 и
и 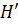 . Вершины
. Вершины 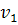 и
и 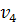 должны соединяться ребром, которое проходит либо в
должны соединяться ребром, которое проходит либо в 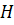 , либо в
, либо в 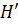 . Эти возможности рассматриваются подобным образом. Пусть ребро
. Эти возможности рассматриваются подобным образом. Пусть ребро 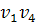 проходит в
проходит в 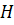 , тогда вершины
, тогда вершины 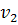 ,
, 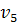 должны соединяться ребром в
должны соединяться ребром в 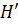 . Тогда вершины
. Тогда вершины 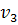 и
и 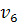 соединить без пересечения других ребер нельзя.
соединить без пересечения других ребер нельзя.
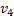
|
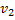
|
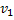
|
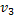
|
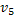
|
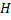
|
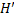
|
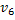
|
Таким образом, показано, что графы 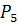 и
и 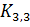 непланарны.
непланарны.
Что и требовалось доказать.
Определение.Рассмотрим укладку планарного графа на плоскости. Тогда ребра графа разрезают плоскость на связные области, которые будем называть гранями укладки.
Теорема Эйлера
Рассмотрим связный планарный граф 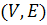 с числом вершин
с числом вершин 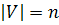 и числом ребер
и числом ребер 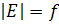 . Число граней в любой планарной укладке данного графа равна k. Данные три параметра связаны соотношением:
. Число граней в любой планарной укладке данного графа равна k. Данные три параметра связаны соотношением:
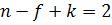
Доказательство:
Доказательство будем проводить по индукции по числу граней в укладке планарного графа.
1-ый шаг индукции. Рассмотрим граф с единственной гранью. Связный граф с единственной гранью – дерево (так как грань одна, то циклов в графе быть не может, поскольку каждый цикл разрезает плоскость на 2 области). Известно, что в дереве на 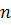 вершинах
вершинах 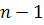 ребро. Подставив данные значения в формулу, получаем тождество:
ребро. Подставив данные значения в формулу, получаем тождество:
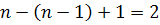
k-ый шаг индукции. Допустим, что утверждение доказано для планарного связного графа с числом граней k-1>1. Рассмотрим планарный граф, с числом граней k. Так как k 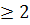 , то в таком графе есть цикл. Рассмотрим грань H, в которой граница - некоторый цикл
, то в таком графе есть цикл. Рассмотрим грань H, в которой граница - некоторый цикл 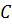 .
.
H
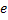
Пусть 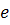 – некоторое ребро этого цикла. Удалим это ребро. Получим связный граф с тем же самым числом вершин
– некоторое ребро этого цикла. Удалим это ребро. Получим связный граф с тем же самым числом вершин 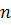 , с числом ребер на
, с числом ребер на 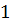 меньше (
меньше ( 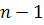 ) и с числом граней k-1. Тогда, применяя предположение индукции:
) и с числом граней k-1. Тогда, применяя предположение индукции:
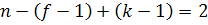
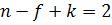
Что и требовалось доказать.
Определение. Операция подразбиения ребра 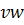 называется преобразование этого ребра, при котором между вершинами
называется преобразование этого ребра, при котором между вершинами  и
и 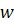 вставляется новая вершина
вставляется новая вершина 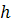 .
.
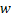
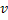
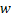
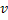
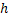
Определение. Операция стягивания обратна операции подразбиения:
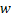
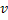
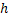
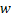
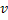
(вершина h в графе смежна только вершинам v и w)
4.6 Критерий Понтрягина-Куратовского планарности графа.
Граф является планарным тогда и только тогда, когда он не содержит графов, гомеоморфных графам 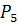 и
и 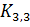
Определение. Пара графов называются гомеоморфными, если один граф можно получить из другого с помощью последовательности операций подразбиения и стягивания ребер.
Пример. Следующие два графа гомеоморфны: первый граф можно стянуть по вершине 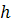 .
.
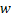
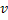
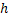
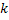
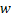
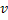
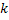
Здесь проводится доказательство только необходимости критерия.
Если граф планарен, то все его подграфы очевидно планарны. Операция стягивания и подразбиении очевидно не меняет планарности графа. Поэтому, если бы планарный граф содержал подграф, гомеоморфный 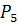 и
и 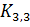 , то рассмотренные графы
, то рассмотренные графы 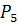 и
и 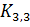 были бы планарными. А по доказанному они такими не являются.
были бы планарными. А по доказанному они такими не являются.
Что и требовалось доказать. Доказательство достаточности можно найти в указанной литературе.
|
из
5.00
|
Обсуждение в статье: Поиск в глубину. Нахождение остовного дерева с помощью поиска в глубину |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

