Главные позиционные задачи

УЧЕБНОЕ ПОСОБИЕ

 

по курсу «Начертательная геометрия»

 

Методические указания по решению задач в рабочей тетради

 

 

Тольятти 2007

Содержание

 

Модуль №1. 4

Точка. 4

Задача №1. 4

Задача №2. 7

Линия. 9

Задача №3. 9

Задача №4. 9

Задача №6. 10

Задача №8. 11

Задача №10. 12

Задача №11. 13

Задача №13. 14

Задача №12. 16

Модуль №2. 19

Плоскость. 19

Задача №17. 19

Задача №18. 21

Задача №20. 24

Задача №21. 26

Задача №22. 26

Задача №23. 28

Задача №24. 31

Задача №25. 31

Задача №26. 34

Задача №27. 36

Задача №30. 37

Задача №31. 37

Поверхность. 41

Задача №32. 41

Задача №23. 42

Задача №34. 44

Задача № 35. 47

Задача №36. 50

Задача №37. 50

Задача №38. 53

Задача №40. 57

Задача №41. 57

Задача №42. 60

Задача №43. 63

Задача №46. 65

Задача №47. 69

Задача №47. 72

Задача №48. 73

Задача №50. 75

Модуль №3. 79

Главные позиционные задачи. 79

Решение задач по 1 и 2 алгоритмам.. 79

Задача №55. 79

Задача №57. 80

Задача №58. 81

Задача №60. 84

Задача №61. 92

Задача №64. 94

Задача №67. 96

Задача №71. 99

Задача №73. 103

Задача №76. 106

Задача №78. 108

Модуль №4. 110

Метрические задачи. 110

Задача №81. 110

Задача №82. 111

Задача №83. 112

Задача №84. 113

Задача №85. 113

Задача №86. 114

Задача №87. 115

Задача №88. 116

Задача №89. 116

Задача №90. 118

Задача №91. 119

Задача №92. 120

Задача №93. 121

Задача №95. 122

Метод введения новой плоскости проекций. 123

Задача №100. 123

Задача №101. 126

Задача №102. 127

Задача №103. 130

Задача №104. 130

Задача №105. 132

Задача №106. 134

Задача №107. 136

Задача №107. 138

Задача №109. 141

Задача №110. 145

Метод вращения вокруг проецирующей оси. 148

Задача №115. 148

Задача №116. 149

Задача №117. 150

 

Модуль №1

Точка

Задача №1

 

Построить комплексные чертежи точек: А(15,30,0), В(30,25,15), С(30,10,15), D(15,30,20)

Решение задачи разделим на четыре этапа.

1. А(15,30,0); x_A= 15 мм; y_A = 30мм; z_A = 0.

Как Вы думаете, если у точки А координата z_A=0, то какое положение она занимает в пространстве?

Рис. 1.1

Так выглядит комплексный чертеж точки А построенный по заданным координатам

Если у точки одна координата равна нулю, то точка принадлежит одной из плоскостей проекции. В данном случае у точки нет высоты: z = 0, следовательно точка А лежит в плоскости П₁.

На комплексном чертеже оригинал (т.е. сама точка А) не изображается, есть только ее проекции.

 

2. В(30,25,15) и С(30,10,15).

На втором этапе объединим построение двух точек.

x_B = 30мм; x_C = 30мм

y_B = 35мм; y_C = 10мм

z_B = 15мм; z_C = 15мм

У точек В и С: x_B = x_C = 30мм, z_B = z_C = 15мм

 

а) Координаты х точек одинаковы, следовательно, в системе П₁ – П₂ проекции точек лежат на одной линии связи (рис. 1.2),

Рис. 1.2

б) Координаты z точек совпадают, (обе точки одинаково удалены от П₁ на 15мм,) т.е. они расположены на одной высоте, следовательно на П₂ проекции точек совпадают: В₂ = (С₂).

в) Для определения видимости относительно П₂ смотрим на рис. 1.3. Наблюдатель видит точку В, которая закрывает собой точку С, т.е. точка В расположена ближе к наблюдателю, поэтому на П₂ она видима. (См. М1 - 13 и 16).

Рис. 1.3

В системе П₂П₃ проекции точек также лежат на одной линии связи и видимость определяется по стрелке (рис. 1.2).

Точки В и С - называются фронтально конкурирующими.

3. D(15,30,20); x_D = 15мм; y_D = 30мм; z_D = 20мм.

а) На этом комплексном чертеже (рис. 1.4) построены три проекции точки D(D₁, D₂, D₃).

Все три координаты имеют числовые значения, отличные от нуля, поэтому точка не принадлежит ни одной плоскости проекций.

Рис. 1.4

б) Совместим пространственное изображение А и D (рис. 1.5). В системе П₁-П₂ проекции точек А и D лежат на одной линии связи, только точка D выше точки А, следовательно D - видима, а А - невидима (видима на П₁ та точка, которая расположена выше)

Рис. 1.5

На четвертом, завершающем этапе, соединим все три фрагмента комплексных чертежей точек А,В,С,D в один общий.

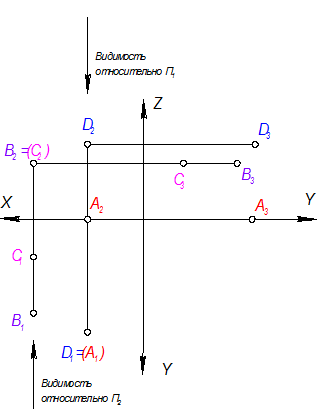
Рис. 1.6

Точки А и D - называются горизонтально конкурирующими.

Рис. 1.7

 

 

Задача №2

 

На заданных линиях связи построить проекции точек В и С: точка В расположена выше точки А на 10мм и ближе к наблюдателю на 15мм; точка С расположена ниже точки А на 10мм и ближе к плоскости П₂ на 5мм.

Решение задачи осуществляется на безосном комплексном чертеже.

1. Распределим линии связи для точек В и С

2. Проведем вспомогательные линии ^ А₁А₂, пересекая линии связи точек В и С.

Верхняя горизонтальная линии от А₂ будет определять уровень точек В и С относительно П₁, по сравнению с точкой А, т.е. "выше - ниже" А:

Точка В выше на 10мм, чем точка А относительно П₁

Точка С ниже на 10мм, чем точка А относительно П₁

3. Нижняя горизонтальная линия от А₁ будет границей расположения точек В и С относительно П₂, по сравнению с точкой А, т.е. "ближе - дальше" от наблюдателя:

Точка В ближе на 15мм к наблюдателю, чем А,

Точка С дальше от наблюдателя, т.е. ближе к П₂ на 5мм, чем точка А.

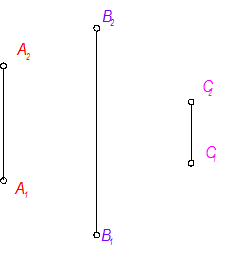
4. Убираем все вспомогательные построения.

 

Задача решена.

Линия

Задача №3

Для решения этой задачи, при необходимости, можно воспользоваться Модулем №1(стр. 20)

 

Задача №4

Построить проекции отрезка АВ горизонтали h(h₁h₂) || П₁ если Ðb=30°, |АВ| = 40мм, точка В удалена от П₂ дальше, чем точка А.

Решить эту задачу, значит построить точка В(В₁В₂).

h₂ ^ линии связи,

h₁ - проецируется в истинную величину;

Ðb - угол наклона горизонтали к П₂ проецируется без искажения.

Алгоритм построения.

1. Горизонталь начинаем строить с фронтальной плоскости: h₂ ^ лин. связи. Можно ли отложить на этой линии 40мм и построить точку В₂? Нельзя, т.к. h₂ проецируется с искажением.

2. На П₁ проведем вспомогательную прямую из А ^ А₁А₂.

3. Построим угол Ðb. Его можно отложить вверх от вспомогательной линии и вниз, но в задаче дано, что точка В удалена от П₂ дальше, чем точка А, поэтому луч для Ðb = 30° откладываем вниз.

4. На этом луче откладываем расстояние, равное 40мм и получаем: h₁ = А₁В₁ = |АВ|

5. Так как мы построили горизонтальную проекцию точки В Þ В₁, то для определения В₂ достаточно провести линию связи до пересечения с h₂ Þ В₂.

 

Задача №6

Построить проекции отрезка |МN| =30мм горизонтально проецирующей прямой при условии, что точка В делит отрезок пополам.

1. Горизонтально проецирующая прямая MN параллельна сразу двум плоскостям проекций: П₁ и П₂.

Отложить 15мм вверх и вниз от точки В₂

2. Фронтальная ее проекция – M₂N₂ проецируется без искажения на П₂ и совпадает с линиями связи, а горизонтальная проекция проецируется в точку, которая называется главной проекцией и обладает собирательными свойствами (М₁=N₁=В₁).

B1=N1=M1 – горизонтально конкурирующие точки

 

Задача №8

Определить истинную длину отрезка АВ и углы его наклона к плоскостям проекций П₁ и П₂

1. Анализ условия: ни одна из проекций отрезка АВ не || и не ^ линиям связи, значит задана прямая общего положения (Модуль №1, стр. 20).

A₁B₁ – первый катет. Перпендикуляр к A₁B₁ можно провести как из точки A₁ так и из В₁

2. Двухкартинный чертеж Монжа обратим, поэтому для нахождения натуральной величины отрезка АВ применяют метод прямоугольного треугольника. (Модуль №1, стр. 14).

А₁А₀ – второй катет. Гипотенуза А₀В₁ – это натуральная величина |AB| - это натуральная величина |AB|. Угол a - есть угол наклона AB к П_1.

Аналогично, можно найти натуральную величину отрезка АВ и угол (b) наклона данного отрезка АВ к П₂, построив прямоугольный треугольник на П₂. Самостоятельно.

 

Задача №10

Построить горизонтальную проекцию отрезка АВ, если Ðb = 20° (угол наклона к П₂), точка В дальше от П₂, чем точка А.

Решение задачи сводится к построению горизонтальной проекции точки В Þ В₁, т.е. надо определить разность удаления концов отрезка АВ до П₂.

Как это можно сделать?

Только построив прямоугольный треугольник на П₂ для этого информации?

Да, т.к. есть один катет А₂В₂ и угол наклона гипотенузы к нему.

Провести линию связи из В₂ т.к. В₁-В₂ находятся на одной линии связи. Провести из точки А вспомогательную прямую ^ А₁А₂ т.к. по условию точка В дальше от П₂, чем точка А.

А₂В₂ - первый катет. Перпендикуляр (второй катет) можно проводить из любой точки А₂ или В₂.

Построить из точки А₂ угол 20° (перенести графически) с помощью циркуля.

В₂В₀ (Dу) - второй катет. Гипотенуза А₂В₀ -натуральная величина отрезка АВ.

В₂В₀ - значение второго катета отложить от точки В Þ В₁.

 

Задача №11

Через точку А провести прямую m ° n, если EÎm, CÎn, точка Е расположена перед С на 10мм.

Прямые m и n скрещивающиеся, значит у них нет общих точек. Точки Е и С - фронтально конкуририрующие, т.е. точки С и Е лежат на одном ^ к П₂, поэтому С₁ и Е₁ лежат на одной линии связи.

Продлите линию связи из точки С₁. От С₁ отложите 10 мм ближе к наблюдателю Þ получим точку Е₁

Через две точки А₁ и Е₁, проводим m₁, точка Е(Е₁) расположена ближе к наблюдателю, значит на П₂ фронтальная проекция точки С(С₂) - невидима, взять в скобки..

Точки D и F - горизонтально конкурирующие, построить их фронтальные проекции и определить видимость самостоятельно (Модуль №1, стр.26).

 

Задача №13

Построить горизонтальную проекцию плоской кривой m.

1₁ = ?, 2₁ = ?, m₁ = ?

Для построения проекций плоской кривой применяется метод хорд. Кривая считается плоской, если проекции точки пересечения проекций одноименных хорд лежат на одной линии связи (Модуль №1, стр. 29).

Строим хорду АВ на П₁ и П₂. На П₂ строим фронтальную проекцию хорды 1₂С₂.

А₂В₂ Ç 1₂С₂ = 3₂

Опустив линию связи из точки 3₂, находим точку 3₁. Точка 3(3₂,3₁) позволит построить горизонтальную проекцию хорды 1С.

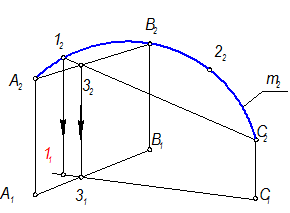
Проводим линию связи из точки 1₂ до пересечения с продленной прямой 3₁С₁ Þ 1₁

Плавной кривой соединим точки А₁, 1₁, В₁, получаем часть горизонтальной проекции кривой m.

Аналогично, строится точка 2_1.

Объединим все построения на одном чертеже, обозначим горизонтальную проекцию кривой m_1.

Чем больше точек брать на кривой АВ, тем точнее построение (5-6 точек).

 

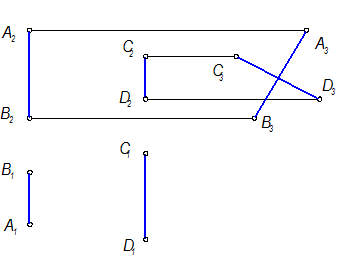
Задача №12

Определить взаимное положение отрезков прямых АВ и CD.

На 3-х картинном чертеже Монжа размеры по оси y (размеры ширины) на П₁ и П₃ остаются неизменными.

Точка С₃ в системе П₂- П₃ (на линии связи ^ оси Z), взята произвольно, т.к. чертеж безосный. Все остальные проекции точек А,В,D на П₃ жестко связаны с точкой С₃

(Модуль №1, стр.15).

Построение точки D₃

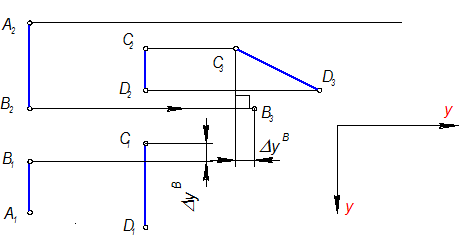
Построение точки В₃

Построение точки А₃

Решение задачи 14 см. Модуль №1, стр. 31.

Решение задачи 15 см. Модуль №1, стр. 34

 

 

Модуль №2

Плоскость

Задача №17

В плоскости достроить недостающие проекции точки и прямой:

S(АВС) É l(l₂); l = ?; D(D ) ; D = ?

В основе решения задачи лежит свойство принадлежности точки и прямой плоскости

(Модуль №2, стр.2).

l Ì S, значит проходит через две точки этой плоскости 1 и 2.

точка 1 Î АВ, 1₂ Î А₂В₂ Þ 1₁ Î А₁В₁

точка 2 Î АС, 2₂ Î А₂С₂ Þ 2₁ Î А₁С₁

1. Построим горизонтальные проекции точек 1 и 2(с помощью линий связи) Þ 1₁ и 2₁

2. Через точки 1 и 2 проведем горизонтальную проекцию прямой – l.

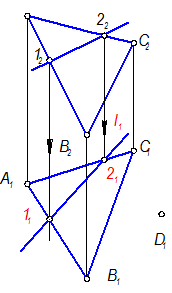
Очень важно не перепутать принадлежность точек своим отрезкам.

 

Как построить точку D?

Заметим, что точка D находится за пределами треугольника, но, тем не менее, принадлежит плоскости S, т.к. любая плоскость безгранична в пространстве, треугольник - это только ее определитель, с помощью которого она задана.

Так с чего начать? Обычно студенты предлагают провести линию связи из точки D₁. Действительно D₁ и D₂ находятся на одной линии связи, Хорошо, провели, а дальше?

 

Исходя из свойства принадлежности точки плоскости, через точку D(D₁) нужно провести вспомогательную прямую в плоскости. Сколько таких прямых можно провести? Бесчисленное множество, выбрав наиболее рациональный вариант.

1 вариант

2 вариант

Первый вариант рациональнее, т.к. для вспомогательной прямой нужно строить меньше точек (достаточно построить точку 3, точка А уже есть).

Задача №18

В плоскости достроить недостающие проекции линий:

Г(a || b), l(l₂) Ì Г, l₁ = ?, m(m₁) Ì Г, m₂ = ?

Принадлежность прямой плоскости, в случае, когда она проходит через две точки этой плоскости, была рассмотрена в задаче № 17. В этой задаче проиллюстрируем принадлежность прямой плоскости, если она проходит через одну точку плоскости и параллельна какой-либо прямой, лежащей в плоскости.

l₁ = ? l || a || b

Где взять эту точку? На l₂ можно взять любую точку и построить ее проекции на П₁ по принадлежности к Г (рис. 18.1). Рациональнее взять точку 3₂ (рис. 18.3).

Рис. 18-1

Через прямую 1-2 строим проекции точки 3

Рис. 18-2

Теперь через точку 3₁ проводим l₁ || а₁ и в₁

Рис. 18-3

Как построить m₂?

Следует отметить, что для построения кривой m₂ нужно взять не менее четырех точек.

Рис. 18-4

Точки 4,6,8 строятся без дополнительных построений, с помощью линий связи.

Рис. 18-5

Для построения точки 5 и 7 проводят дополнительные прямые || а и в.

Рис. 18-6

Находим точки 5₂, 7₂.

Рис. 18-7

Все точки соединить плавной кривой Þ m₂

Рис. 18-8

 

Задача №20

Дана плоскость L(h Ç f), АВС Ì L, А₁В₁С₁ = ?

Как построить А₁В₁С₁, зная свойство принадлежности точки и прямой к плоскости? Треугольник АВС надо рассматривать, как фигуру, состоящую из вершин (точек А,В,С) и сторон (отрезков прямых), т.е. следует применить решение предыдущих задач №17 и №18.

Рис. 20-1

Сторона АВ || h, точка А принадлежит f.

A₂ Î f₂ Þ A₁ Î f _, A₂B₂ || h₂ Þ A₁B₁ || h₁ (Рис. 20-2)

Рис. 20-2

Горизонтальная проекция АС строится по двум точкам: А и 1 = А₂C₂ Ç h₂ Þ 1₁ Þ С₁ (Рис. 20-3)

Рис. 20-3

 

Задача №21

Задача решается аналогично, чтобы построить фронтальные проекции точек D,F,E, необходимо построить фронтальные проекци любых двух сторон треугольника (например DF и DE), исходя из свойства принадлежности прямой к плоскости. Для чего следует их продлить до пересечения с Ф, т.е. с m₁ и n₁.

 

Задача №22

Определить угол наклона плоскости S(g) к П₁

А(А₂) Î S. А₁ = ? Ða = ?

Плоскость S задана g - линией ската, но т.к. положение g в плоскости определяется положением горизонтали этой плоскости, то значит можно однозначно утверждать,что данная плоскость задана двумя пересекающимися прямыми Þ S(g) = S(g Ç h) (Модуль №2, стр. 8)

g ^ h Þ h₂ ^ линиям связи, g₁ ^ h₁, h₂ провести через А₂, А₁ находится по принадлежности

горизонтали

Но как определить угол a?

Угол a между g u g₁ - есть угол наклона S ^Ù П₁ = g ^Ù g

g(g₁,g₂) - прямая общего положения

Для определения угла (a) необходима истинная величина линии ската, которую определим методом прямоугольного треугольника (задача №8)

Угол между g и g₁ = Ða.

Если бы не требовалось определить А₁, то угол можно было бы определить и без построения горизонтали. Достаточно задаться любым отрезком на линии ската.

 

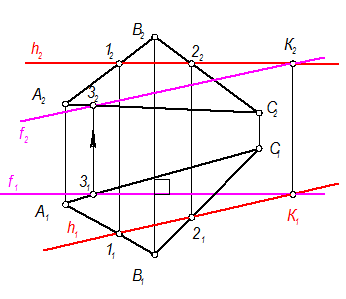
Задача №23

Определить угол наклона плоскости Ф(а || b) к П₂. Ðb = ?

Как определить е - линию наибольшего наклона плоскости Ф к П₂(е ^ f Þ е₂ ^ f₂)? Задача графически сложная, но легко решается, если ее разбить на три этапа (на три задачи), которые встречались на предыдущих страницах:

1) Построить проекции фронтали f (f₁ f₂)

Построить f(f₁,f₂): f₁ ^ линиям связи (в любом месте f₁ Ç а || в), f₂ по принадлежности плоскости Ф

2) Построить проекции линии наибольшего наклона е(е₁ е₂)

Построить е(е ^ f) Þ е₂ ^ f₂. Построить е₂ можно бесконечное множество.

Выбираем наиболее рациональный вариант и достраиваем е(е₁) Ì Ф (по двум точкам 1 и 3).

3) Определить натуральную величину | е| с помощью прямоугольного треугольника. Угол Ðb = между е – е₂ (Ф ^Ù П₂ = е ^Ù е₂)

е(е₁, е₂) – прямая общего положения

 

Задача №24

Эта задача решается аналогично, только алгоритм нужно применить относительно П₁.

 

Задача №25

Окружность k Ì Г(Г₁), A Î k, O - центр окружности.

Построить: k₁ =?, k₂ = ?

Плоскость Г занимает горизонтально проецирующее положение. Г₁ = главная проекция, обладающая собирательными свойствами, поэтому k₁ - прямая линия совпадающая с Г₁. Г имеет угол (a) наклона к П₂, поэтому окружность спроецируется на П₂ с искажением, в виде эллипса.

При этом, какое положение займут большая и малая оси эллипса?

Чтобы построить а₂ и в₂, нужно знать значение радиуса окружности (R), т.к. а₁ = 2´R, в₂ = 2´R.

Точка А принадлежит окружности, поэтому соединив точку А с О Þ R. На какой проекции можно замерить значение радиуса?

Нигде! Т.к. ОА - прямая общего положения.

Методом прямоугольного треугольника определяем натуральную величину радиуса окружности Þ R

а (1,2) - малая ось эллипса

в (3,4) - большая ось эллипса

Эллипс - центрально симметричная замкнутая кривая, следовательно относительно точки О₂ на кривой таких точек как А₂ - четыре.

Теперь плавной кривой соединяем все 8 точек.

Плавной кривой соединить все точки

 

Задача №26

В заданных плоскостях через точку К провести проекции линий уровня

Г(АВС), К Î Г.

Горизонталь плоскости Г должна пройти через две точки плоскости, начинать построение с фронтальной проекции (задача №4)

K₂ Î h₂ ^ линиям связи

h₂ Ç A₂B₂ = 1₂

h₂ Ç B₂C₂ = 2₂

Через 1₁2₁ Þ h₁, Построить К₁ Î h

Построение фронтали f (f₁ f₂) начинают с горизонтальной проекции: через точку К₁ проводят f₁ ^ линиям связи.

f₁ Ç А₁С₁ = 3₁ Þ 3₂; через 3₂ и К₂ Þ f₂.

 

Задача №27

Y(Y₂), К Î Y

Если построение горизонтали начинать с фронтальной проекции ^ линиям связи, как в предыдущей задаче, то h₂ пересечет Y, т.е. не будет принадлежать Y. Как быть? Попробуйте мысленно вращать h || П₁, пока она не совместится с Y₂, это произойдет только тогда, когда горизонталь займет положение фронтально проецирующей прямой.

Y - фронтально проецирующая плоскость.

h ^ П₂ Þ h₂ - точка, h₁ = линиями связи.

f₁ ^ линии связи, f₂ = Y₂

 

Задача №30

Через точку М провести прямую m(m₁ m₂) параллельную плоскостям S(АВС) и Г(Г₁).

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Если плоскость занимает проецирующее положение (Г₁), то проекция прямой параллельна ее главной проекции, т.е. Г₁.

Алгоритм построения.

1. Проведем m₁ || Г₁ через точку М₁, но прямая m || и DАВС, поэтому проведем прямую С₁1₁ || m₁ в DА₁В₁С₁.

2. На П₂ построим С₂1₂ и параллельно этой прямой через точку М₂ проведем m₂: m₂ || C₂1₂

 

Задача №31

Достроить фронтальную проекцию плоскости Г(DEF), если Г(DEF) || Ф(АВС).

Как построить D₂E₂F₂, зная положение о взаимно параллельных плоскостях (Модуль №2, стр.10)? Треугольник DEF надо рассматривать, как фигуру, состоящую из пересекающихся прямых (сторон), чтобы применить решение предыдущей задачи №30. Для определения точек E₂ и F₂ необходимо построить параллельно DАВС две стороны DDEF.

Построить DF(D₂F₂) || DАВС, для чего провести А₁1₁ || D₁F₁

Построить DЕ(D₂F₂) || DАВС, для чего провести C₁2₁ || D­₁E₁

Достроить фронтальную проекцию DDЕF

Очень часто студенты путают построение треугольника, параллельного заданному, с построением треугольника, принадлежащего заданному.

 

DDЕF || DАВС

DDЕF принадлежит Г(АВС)

 

 

Поверхность

Задача №32

Построить три проекции призмы

S(АВС l), если S || П₂, если m Ì S.

m₂ = ? m₃ = ?

Алгоритм построения.

Призма S(АВС,l) – фронтально проецирующая. Ребра l ^ П₂ || П₁, П₃

1. Достроить проекции призмы на П₁ и на П₃.

2. m Ì S -ломаная линия, состоит из двух прямых, которые обозначим тремя точками (1,2,3).

3. На П₂ проекции призмы и линии m совпадают.

4. На П₃ точки 1₃ и 2₃ будут видимыми, так как лежат в плоскости АА’ВВ’, расположенной ближе к наблюдателю.

5. Точка 3₃ расположена в плоскости ВВ’СС’ , которая на П₃ закрыта плоскостями АА’ВВ’ и АА’СС’, следовательно, будет невидимой.

6. Соединим три точки, с учетом видимости, получим профильную проекцию линии m.

 

Задача №23

Построить три проекции цилиндра вращения

Q(i,l), если Q || П₁;

n Ì Q, n₁ = ? n₃ = ?

Алгоритм построения.

Цилиндр вращения Q - горизонтально проецирующий.Образующая l ^ П₁ || П₂ || П₃.

1. Построить проекции цилиндра на П₁, П₂, П₃.

2. Кривая n Ì Q. Разделим фронтальную проекцию кривой на 5 произвольных точек. Точки 3₂ и 5₂ - особые, находятся на крайних образующих; 1₂, 2₂, 4₂ - промежуточные точки.

3. На П₁ все точки совпадают с проекцией цилиндра вращения.

4. Находим проекции точек на П₃. Точки 1₃, 2_3, 3₃ будут видимыми, а точки 4₃, 5₃ - невидимыми. Точки 3₃ и 5₃ не требуют дополнительных построений, т.к. они уже лежат на своих образующих.

5. Соединив точки на П₃ с учетом видимости, получим профильную проекцию кривой n₃.

 

Задача №34

Построить проекции трехгранной призмы Ф(АВС, s), М Î Ф , М₁ = ? Высота призмы 40 мм

Вспомним алгоритм конструирования поверхности: М2-15. Что задано на чертеже?

Проекции геометрической части определителя. Строим дискретный каркас, закон каркаса:

lÇABC, l || s

С какой проекции начнем конструировать линейчатую поверхность? Можно начать с любой, но, учитывая условие задачи (высота 40 мм), начнем построение с фронтальной проекции, проведя 3 образующие || s₂.

Построить проекцию линии обреза на П₂

А₂’В₂’С₂’ - фронтальная проекция линии обреза. С помощью линий связи построить ее горизонтальную проекцию – А₁’В₁’С₁’

Для того, чтобы обвести проекции поверхности основной сплошной линией, необходимо определить видимость.

Точки 1 = 2(1₁ = 2₁) - горизонтально конкурирующие, точка 1 выше, чем точка 2.

Точки В’ = 4(В₂’ = 4₂) - фронтально конкурирующие, точка В ближе к наблюдателю, чем точка 4.

 

Ребро В₁В₁’ частично видимо, т.к. поверхность (в данном случае призма) - это пустотелая геометрическая фигура., имеющая только боковую поверхность.

На П₂ точка М(М₂)- видимая, Î АА’ВВ’. Через точку М(М₂) провести образующую М5(М₂5₂). Точка М(М₁) - невидимая.

 

Задача № 35

Построить проекции пирамидальной поверхности Г(1,2,3, S); А,В Î Г; А₁,В₂=?

Вспомним алгоритм конструирования поверхности: М2-15. Что задано на чертеже?

Проекции геометрической части определителя. Строим дискретный каркас из трех образующих, закон каркаса: l Ç 1,2,3; S Î l

Соединить точки направляющей 1,2,3 с вершиной S, на обоих проекциях. Определить видимость проекций поверхности, точки 4=5(4₂ =5₂) - фронтально конкурирующие точки, точки 6=7(6₂=7₂) - горизонтально конкурирующие точки.

Точка 7 выше, чем точка 6, точка 4 ближе к наблюдателю, чем точка 5.

А Î Г, А₁ = ?

В Î Г, В₂ = ?

Задача №36

Построить проекции пирамидальной поверхности общего вида Y(А,В,С,D,F,S), n Ì Y, n₁ = ?

Задачу 36 решить самостоятельно, учитывая опыт решения предыдущих задач. Ломаную линию

n(n₁) построить по принадлежности соответствующим граням, учитывая видимость проекций

поверхности.

 

Задача №37

Построить проекции конической поверхности общего вида Г(m,S), АÎ Г, ВÎ Г, А₂ = ?, В₁ =?

Коническая поверхность - кривая линейчатая (М2-21, 22), образующая l - прямая линия.

Что задано на чертеже?

Проекции геометрической части определителя. Строим дискретный каркас, закон каркаса:

l Ç m; l É S

Провести конечное число образующих, начиная с очерковых.

Определить видимость проекций поверхности:

точки М=N(М₁=N₁) - горизонтально конкурирующие,

точки 4=7(4₂=7₂) - фронтально конкурирующие,

точка N выше, чем М,

точка 4 ближе к наблюдателю, чем точка 7

А,В Î Г, В₁ =? А₁ =?

Через точки А и В провести образующие.

 

Задача №38

Построить проекции цилиндрической поверхности S(m,s).

h =35 мм, K Î S, K₂ =?, N Î S, N₁ =?

Алгоритм построения.

На чертеже заданы проекции геометрической части определителя цилиндрической линейчатой поверхности.

Закон образования каркаса цилиндрической поверхности: l Ç m, l || s

1. Расстояние между верхним и нижним основаниями равно 35 мм.

2. Через центр направляющей m проведем осевые линии параллельно s на П₁ и на П₂ Þ О₁’, О₂’

3. На направляющей m обозначим 4 точки с учетом видимости.

4. На П₂ проведем две очерковые образующие: 11’(1₂1₂’) и 22’(2₂2₂’) || s₂ и построим фронтальную проекцию цилиндра.

5. На П₁ построим горизонтальную проекцию линии обреза &