Рекомендации к выполнению курсовой работы

С электронных таблиц MS Excel выполнить следующие действия:

1. Ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.

Рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.

3. Вычислить коэффициенты функциональной зависимости, соответствующей варианту задания. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку. Вычислить индекс корреляции.

4. Построить в одной графической области экспериментальные точки и линию тренда. Определить степень достоверности подбора линии тренда и суммарную ошибку.

Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии, линию тренда и график полученной экспериментальной зависимости.

6. Сделать выводы.

Математическая модель поставленной задачи

Метод наименьших квадратов используется при обработке реальных количественных данных, полученных в результате всевозможных научных опытов, технических испытаний, астрономических, геодезических и т.п. наблюдений.

Пусть в результате эксперимента были получены некоторые данные, представленные в виде таблицы:

Необходимо построить аналитическую зависимость, наиболее близко описывающую результаты эксперимента.

Идея метода наименьших квадратов заключается в том, что функцию

Y = f(x, a₀ a₁, ..., a_k)

необходимо подобрать таким образом, чтобы сумма квадратов отклонений измеренных значений y_iот расчетных Y_i была наименьшей (рис. 1):

(1)

Задача сводится к определению коэффициентов a_i из условия (1). Для ее решения необходимо составить систему уравнений

Рис. 1. Геометрическая интерпретация метода наименьших квадратов

Если параметры a_iвходят в зависимость Y = f(x, a₀ a₁, ..., a_k) линейно, то получим систему из k-линейных уравнений с k неизвестными:

(2)

Зная коэффициенты a_i, являющиеся решением системы (2), можно составить искомую функцию Y = f(x, a₀, a₁, ..., a_k).

3.1 Подбор параметров линейной функции

Пусть необходимо определить параметры функции:Y = a₀ + a₁x.

Составим многочлен (1) для заданной функции:

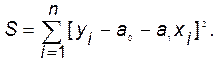
Сформируем систему линейных уравнений (2) решив которую, определим коэффициенты функции Y = a₀ + a₁x:

,

. (3)

Квадратичная функция

Необходимо определить параметры функции: Y = a₀ + a₁ x + a₂ x².

Составим функцию (1):

.

После дифференцирования система уравнений (2) примет вид:

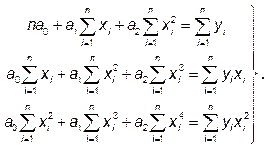(4)

Решив систему (4), найдем значение параметров a_o, a₁, a₂.

3.3. Кубическая функция

Необходимо определить параметры многочлена третьей степени:

Y = a_o + a₁ x + a₂ x² + a₃ x³.

Составим функцию

Система уравнений для вычисления параметров a_o, a₁, a₂, a₃ примет вид:

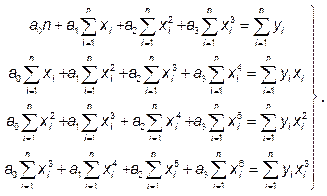(5)

Полином k-й степени

Необходимо определить параметры многочлена k-й степени:

Y=a₀ + a₁x + a₁x² +... + a_k x^k.

Тогда система уравнений для определения параметров a_k принимает вид:

(6)

3.5. Функции, приводимые к линейной

Для вычисления параметров функции Y = ax^b необходимо выполнить некоторые арифметические преобразования:

ln(y) = ln(ax^b) = ln(a) + b ln(x)

и сделать замену

Y = ln(y), X = ln(x), A = ln(a),

которая приведет заданную функцию к линейному виду Y = A + bX, где коэффициенты A и b вычисляются по формулам (3.3) и, соответственно, a = e^A.

Аналогично можно подобрать параметры функции вида Y = ae^bx.

Прологарифмируем заданную функцию:

ln(y) = ln(a) + bx ln(e) Þ ln(y) = ln(a) + bx.

Проведем замену: Y =ln(y), A =ln(a) и получим линейную зависимость Y = bx + A. По формулам (1.3) найдем A и b, а затем вычислим a = e^A.

В табл. 1.20, приведены примеры еще нескольких функций, которые сводятся к линейной функции элементарными заменами.

Преобразование функций Y = f(x, a,b) к виду Y = Ax + b

Функция	Замена	Функция	Замена	Функция	Замена

3.6. Подбор параметров функции y = ax^be^cx