III. Пределы. Производные

 

1. Дана последовательность: -1/2, 1/4, -1/8, 1/16… Найти а_n (n = 1,2,3…). = в) а_n =

2. Пустьa(х) и b(х) – бесконечно малые при х®a. Если 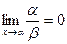, то = в) a - бесконечно малая высшего

Порядка по сравнению с b

3. Вычислить lim = б) ¥

х®3+0

4. Вычислить lim = г) 0

х®¥

5. Числовая последовательность {n²} является: = а) возрастающей, неограниченной

6. Найти по правилу Лопиталя lim = а) 1/5

х®p

7. Найти lim2^1/(х-1)

х®1-0 = б) 0

8. Вычислить lim (cosx)^sinx

х®0 = в) 1

9. Вычислить lim

х®0 = в) -1/2

10. Найти область определения функции = б) (-¥;1)È(1;2)È(2;+¥)

11. Установите точки разрыва функции = а) -3;2

12. Определите точки разрыва функции = а) ±1

13. Кривая имеет асимптоты = г) у=1; х=2

14. Какая функция не является бесконечно малой функцией при х®0. = а) е^-х

15. Какая функция не является бесконечно малой функцией при х®¥. = б) 2^1/х

16. Функция sin2x и tg3x при х®0 является: бескон.малыми. одного порядка

17. Вычислить lim = в) е¹²

х®¥

18. Кривая у = х² – 3х возрастает на интервале = г) (3/2;+¥)

19. Функция имеет разрыв в точках: = д) х=2

20. Кривая у = 1/х является выпуклой на интервале: (-¥;0)

21. Найти точки экстремума функции г) х=0 – т. макс

22. На интервале (1;+ ¥) кривая б) возрастает, вогнутая

23. Восстановить пропущенный сомножитель

 

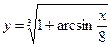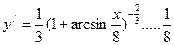, = в)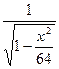

24. Найти асимптоты графика функции б) у = х

25. Найти у^/_х, если х = ln t = в) t

у = t

 

26. Найти производную 10-ого порядка функции у = х¹⁰ = д) 10!

 

27. Найти производную у = (5х² + 10х)² = г) у = 20(5х² + 10х)(х+1)

 

28. Найти у^/_х если х = t³ + 3t + 1 = б)

у = 3t⁵ + 5t³ + 1

29. Найти производную n-ого порядка функции у = 5^х = г) у⁽ⁿ⁾ = 5^xlnⁿ5

30. Найти дифференциал функции = б)

31. Вычислить = а) 0

32. Числовая последовательность является = г) возрастающей, неограниченной

33. Кривая у = имеет асимптоты = г) у=1; х=2

34. Какая из функций не является бесконечно малой функцией при х ® 0? = а) е^-х

35. Найти область определения функции у = б) х £ 2

36. Вычислить lim5/(2х – 2)² = в) ¥

х®1

37. Числовая последовательность является = а) убывающей, ограниченной

38. Вычислить = а) -1

39. Функция убывает на интервале = б) х < 2

40. Кривая у = lnx является вогнутой на интервале = г) всюду выпукла в области определения

41. Установите соответствие

Функция Точки разрыва

1) у = А) х = 1

2) у = Б) х = +1; х = -1; х = 0

3) у = 1/ln|x| В) х = 0; х = -1

4) у = 1/х²(х+1)² Г) точек разрыва нет

А) 1А,2Г,3Б,4В

42.Установить соответствие

Предел: Результат:

1) А) 1

2) Б) 2

3) В) ¥

4) . Г) 0

Г) 1В,2Г,3Б,4А

43. Производная «n»-ого порядка от функции у = е^кх равна = г) у⁽ⁿ⁾ = кⁿ e^кх

44. Установите соответствие

Функция Производные

1) у = 2cos3x А) у^/ = -3sin6х

2) у = cos²3x Б) у^/ = 6sin3х/cos²3x

3) у = 2/cos3x В) у^/ = 6/cos²3x

4) у = 2tg3х Г) у^/ = -6sin3x.

Б) 1Г,2А,3Б,4В

45. Восстановите пропущенные сомножители в производной заданной функции

= в) arcrg²( )

46. Найти предел функции lim2x/(x²+2x+1) по правилу Лопиталя

x®¥ = г) 0

47. Приращение Dу функции у = f(х) и дифференциал функции при Dх®0 является

бесконечно малыми: а) эквивалентными

48. Установите соответствие на интервале (а, в)

1) достаточное условие возрастания функции А) у^/ < 0

2) достаточное условие убывания функции Б) у^// < 0

3) достаточное условие выпуклости функции В) у^/ > 0

4) достаточное условие вогнутости функции Г) у^// > 0

В) 1В,2А,3Б,4Г

49. Какая из функций не является бесконечно большой

функцией при х ® +0 = а) е^-2х

50. Функции sin2x и tg²3х при х®0 являются: г) sin2x – б.м. низшего порядка

51. Вычислить lim(1+3/n) = г) е^3/4

n®¥

52. Установить соответствие

Функция Точки разрыва

1) у = 1/(х²-1) А) х=1

2) у = е^х Б) х=+1; х=-1

3) у = ln|x| В) х=0

4) у = 1/(x-1)² Г) точек разрыва нет.

Д) 1Б,2Г,3В,4А.

53. Кривая у = 1/х является вогнутой на интервале = б) (0;+¥)

54. Установить соответствие

Функция Производная

1) у = ln²(1-x) А) у^/ = -2/(1-х)²

2) у = 1-x Б) у^/ = -1

3) у = -2ln(1-x) В) у^/ = -2ln(1-x)/(1-х)

4) у = 2/(x-1) Г) у^/ =2/(1-х)

Д) 1В,2Б,3Г,4А.

55. Установите пропущенные сомножители в производной заданной функции

у = arctg⁴( ) у^/ = 4 arctg³( )…(-1/( )) = г) 1/(1+ )

56. Установить соответствие

Функция Производные

1) у = U*V А) у^/ = U^/+V^/

2) х = х(t) Б) у^/ = у^/_(t)/x^/_(t)

у = у(t)

3) у = U + V В) у^/ = U^/* V+ V^/* U

4) у =U/V Г) у^/ =0

5) у = С Д) у^/ = (U^/* V+ V^/* U)/V²

Б) 1В, 2Б, 3А, 4Д, 5Г

57. Найти область определения функции у = 1/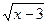

а) х > 3