Ток смещения (электродинамика)

Ток смещения.

Классическая электродинамика

Электричество · Магнетизм

[показать]Электростатика   [показать]Магнитостатика   [показать]Электродинамика   [показать]Электрическая цепь   [показать]Ковариантная формулировка   [показать]Известные учёные

См. также: Портал:Физика

Ток смещения или абсорбционный ток — величина, прямо пропорциональная скорости изменения электрической индукции. Это понятие используется в классической электродинамике. Введено Дж. К. Максвеллом при построении теории электромагнитного поля.

Введение тока смещения позволило устранить противоречие^[1] в формуле Ампера для циркуляции магнитного поля, которая после добавления туда тока смещения стала непротиворечивой и составила последнее уравнение, позволившее корректно замкнуть систему уравнений (классической) электродинамики.

Строго говоря, ток смещения не является^[2] электрическим током, но измеряется в тех же единицах, что и электрический ток.

Точная формулировка

В вакууме, а также в любом веществе, в котором можно пренебречь поляризацией либо скоростью её изменения, током смещения (с точностью до универсального постоянного коэффициента) называется^[3] поток вектора быстроты изменения электрического поля через некоторую поверхность^[4] :

(СИ)

(СГС)

В диэлектриках (и во всех веществах, где нельзя пренебречь изменением поляризации) используется следующее определение:

(СИ)

(СГС),

где D — вектор электрической индукции (исторически вектор D назывался электрическим смещением, отсюда и название «ток смещения»)

Соответственно, плотностью тока смещения в вакууме называется величина

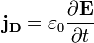(СИ)

(СГС)

а в диэлектриках — величина

(СИ)

(СГС)

В некоторых книгах плотность тока смещения называется просто «током смещения».

 

5. Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением

(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены v → -v.
Монохроматическая волна − распространение колебаний с определённой частотой ω. В случае одномерного распространения волны вдоль оси x формула монохроматической волны имеет вид

u(x,t) = Asin(ωt − xv).

Длина волны λ − путь, пройденный возмущением (состоянием с определённой фазой) за время равное периоду колебаний T

λ = vT.

Волновое число

k = 2π/λ.

Частота ω и период колебаний T связаны соотношением

ω = 2π/T.

Эквивалентные формулы для монохроматической волны, распространяющейся вдоль оси x

u(x,t) = Asin(ωt − kx) = Asinω(t − x/v) = Asin2π(t/T − x/λ).

Сферическая волна.

u(r,t) = (A/r)sin(ωt − kr).

Стоячая волна. При наложении монохроматических волн одинаковой частоты образуется устойчивая картина результирующих колебаний с характерными максимумами и минимумами.

Стоячая волна образуется в системах с двумя жёстко закреплёнными точками. При отражении фаза волны меняется на π и происходит интерференция падающей и отраженной волн.

Падающая волна	u1 = Asin(ωt + kx)
Отражённая волна	u2 = Asin(ωt − kx + π)
Стоячая волна	u1 + u2 = A(x)cosωt	(2)

Соотношение (2) можно получить, используя формулу

sinα − sinβ = 2sin[(α − β)/2] cos[(α + β)/2]

и положив 2Asin(2πx/λ) = A(x), A(x) − амплитуда стоячей волны.

Возмущения от электромагнитных сил

Преимуществами электромагнитных датчиков являются отсутствие механического и электрического контакта датчика и изделия интегральные, усредненные по некоторой площади результаты измерениявозможность применения для стыковых соединений без разделки кромок, а также для стыковых соединений с наложенным на обратной стороне швом возможность применения для изделий из магнитных и немагнитных металлов малые габаритные размеры простота конструкции. Основной недостаток датчиков рассматриваемого типа — влияние на выходной сигнал большого количества возмущений (электромагнитных помех и превышения кромок свариваемых элементов).  [c.112]

Окружим исследуемый источник электромагнитных колебаний S воображаемой поверхностью а и рассмотрим возмущение в точке Р, находящейся вне указанной поверхности (рис.6.1), как  [c.256]

 

6.Электромагнитная волна представляет собой электромагнитное возмущение, распространяющееся, как упоминалось в 3, в вакууме со скоростью с, а в среде — со скоростью v = /j/ ep, где е — диэлектрическая проницаемость вещества, ар — его магнитная проницаемость. С этим электромагнитным возмущением связана энергия, плотность которой (т. е. энергия, заключенная в единице объема)  [c.37]

Из изложенной кратко теории Максвелла следует, что электромагнитное возмущение должно распространяться в диэлектрике со скоростью V = с/ / ер,. Для вакуума е = р, = 1, т. е. скорость распространения в немэлектромагнитной волны с = 3-10 м/с, другими словами, она совпадает соскоростью света. Это основное заключение привело Максвелла к мысли, что свет представляет собой электромагнитное явление. Написанное вышесоотношение Максвелла и = позволяет определить также фазовую скорость  [c.39]

Так как электромагнитное возмущение распространяется во все стороны от диполя с одинаковой скоростью с (предполагается, что диполь находится в вакууме), то время прохождения волны до всех точек, удаленных от диполя на одно и то же расстояние I, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. волна, излучаемая диполем, является сферической.  [c.10]

При нагревании тел часть тепла в результате атомных возмущений неизбежно преобразуется в лучистую энергию. Носителями лучистой энергии являются электромагнитные волны или в другом представлении фотоны (кванты энергии). Скорость перемещения этих носителей в вакууме составляет около 300-10 м сек. Результирующий тепловой поток отизлучающей среды с абсолютной температурой К к поверхности, средняяабсолютная температура которой равна Тс определяется по формуле, построенной на законе Стефана-Больцмана  [c.135]

Опять нужно подчеркнуть, что рассмотренный пример является чисто гипотетическим, но Служит для иллюстрации общего случая. В общем случае точные рещения можно найти только для уравнений, относящихся к независимым полям. Более сложные уравнения для взаимодействующих систем обычно рассматриваются с помощью некоторых методов теории возмущений, при применении которых члены взаимодействия предполагаются малыми. Этот метод приемлем для случая взаимодействия между электромагнитным полем и обычной материей, но в некоторых известных случаях константы связи столь велики, что метод становится неприменимым. Разработка новых методов рещения таких задач составляет одну из основных проблем современноАнглийский ученый Джеймс Максвелл на основании изучения экспериментальных работ Фарадея по электричеству высказал гипотезу о существовании в природе особых волн, способных распространяться в вакууме. Эти волны Максвелл назвал электромагнитными волнами. По представлениям Максвелла: при любом изменении электрического поля возникает вихревое магнитное поле и, наоборот, при любом изменении магнитного поля возникает вихревое электрическое поле. Однажды начавшийся процесс взаимного порождения магнитного и электрического молей должен непрерывно продолжаться и захватывать все новые и новые области в окружающем пространстве (рис. 30). Процесс взаимопорождения электрических и магнитных полей происходит во взаимно перпендикулярных плоскостях. Переменное электрическое поле порождает вихревое магнитное поле, переменное магнитное поле порождает вихревое электрическое поле.

Электрические и магнитные поля могут существовать не только в веществе, но и в вакууме. Поэтому должно быть возможным распространение электромагнитных волн в вакууме.

Условием возникновения электромагнитных волн является ускоренное движение электрических зарядов. Так, изменение магнитного поля происходит при изменении тока в проводнике, а изменение тока происходит при изменении скорости зарядов, т. е. при движении их с ускорением. Скорость распространения электромагнитных волн в вакууме, по расчетам Максвелла, должна быть приблизительно равна 300 000 км/с.

Впервые опытным путем получил электромагнитные волны немецкий физик Генрих Герц, использвав при этом высокочастотный искровой разрядник (вибратор Герца). Герц опытным путем определил также скорость электромагнитных волн. Она совпала с теоретическим определением скорости волн Максвеллом. Простейшие электромагнитные волны — это волны, в которых электрическое и магнитное поля совершают синхронные гармонические колебания.

Конечно, электромагнитные волны обладают всеми основными свойствами волн.

Они подчиняются закону отражения волн: угол падения равен углу отражения. При переходе из одной среды в другую преломляются и подчиняются закону преломления волн:отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух данных сред, равная отношению скорости электромагнитных волн в первой среде к спорости электромагнитных волн во второй среде, и называется показателем преломления второй среды относительно первой.

Явление дифракции электромагнитных волн, т. е. отклонение направления их распространения от прямолинейного, наблюдается у края преграды или при прохождении через отверстие. Электромагнитные полны способны к интерференции. Интерференция — это способность когерентных волн к наложению, в результате чего волны в одних местах друг друга усиливают, а в других местах — гасят. (Когерентные волны — это водны, одинаковые по частоте и фазе колебания.) Электромагнитные волны обладают дисперсией, т. е. когда показатель преломления среды для электромагнитных волн зависит от их частоты. Опыты с пропусканием электромагнитных волн через систему из двух решеток показывают, что эти волны являются поперечными.

При распространении электромагнитной волны векторы напряженности и магнитной индукции перпендикулярны направлению распространения волны и взаимно перпендикулярны между собой (рис. 31).

Возможность практического применения электромагнитных волн для установления связи без проводов продемонстрировал 7 мая 1895 г. русский физик Александр Степанович Попов. Этот день считается днем рождения радио. Для осуществления радиосвязи необходимо обеспечить возможность излучения электромагнитных волн. Если электромагнитный волны возникают в контуре из катушки и конденсатора, то переменное магнитное поле оказывается связанным с катушкой, а переменное электрическое поле — сосредоточенным между пластинами конденсатора. Такой контур называется закрытым (рис. 32, а). Закрытый колебательный контур практически не излучает электромагнитные волны в окружающее пространство. Если контур состоит из катушки и двух пластин плоского конденсатора, то под чем большим углом развернуты эти пластины, тем более свободно выходит электромагнитное поле в окружающее пространство (рис. 32, б). Предельным случаем раскрытого колебательного контура является удаление пластин на противоположные концы катушки. Такая система называется открытым колебательным контуром (рис. 32, в). В действительности контур состоит из катушки и длинного провода — антенны.

Энергия излучаемых (при помощи генератора незатухающих колебаний) электромагнитных колебаний при одинаковой амплитуде колебаний силы тока в антенне пропорциональна четвертой степени частоты колебаний. На частотах в десятки, сотни и даже тысячи герц интенсивность электромагнитных колебаний ничтожно мала. Поэтому для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до сотен мегагерц.

 

 

7 Свободные и вынужденные электромагнитные колебания. Резонанс.

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения. Простейшей системой, где могут возникнуть и существовать электромагнитные колебания, является колебательный контур. Колебательный контур — это система, состоящая из катушки индуктивности и конденсатора (рис. 41, а). Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. 41, б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет течь в ту же сторону и перезарядит конденсатор (рис. 41, в). Ток в данном направлении прекратится, и процесс повторится в обратном направлении (рис. 41, г). Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора в энергию магнитного поля катушки с током , и наоборот.

Период электромагнитных колебаний в идеальном колебательном контуре (т. е. в таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по

формуле Томсона . Частота с периодом связана обратно пропорциональной зависимостью

В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для практического применения важно получить незатухающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют генератор незатухающих колебаний, который является примером автоколебательной системы.

 

Колебательный контур.Дж.Генри (1842 г.) –установил колебательный характер разряда конденсатора (открыл ЭМК).Электромагнитные колебания (ЭМК) - это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи.

Виды электромагнитных колебаний:

1. Свободные ЭМК – колебания, происходящие под действием внутренних сил (затухающие).

2. Вынужденные ЭМК – колебания в цепи под действием внешней периодически изменяющейся электродвижущей силы (не затухающие).

 

1. Свободные электромагнитные колебания.

Простейшей электрической системой, способной совершать свободные колебания, является колебательный контур.

Колебательный контур – цепь, состоящая из катушки и конденсатора, соединенных последовательно.

L – индуктивность катушки[Гн]

C – электроёмкость конденсатора [Ф]

 

Свободные электромагнитные колебания возникают в колебательном контуре после однократного подведения энергии. Это можно сделать, например, зарядив конденсатор от источника.

Т.к. обкладки конденсатора замкнуты на катушку, то конденсатор начнет разряжаться. Этот ток создаст магнитное поле катушки.

По мере увеличения тока и уменьшения напряжения на конденсаторе энергия электрического поля WЭ преобразуется в энергию магнитного поля катушки WМ.

В момент полной разрядки конденсатора ток в катушке и энергия магнитного поля достигают своего максимального значения.

Далее ток начинает убывать. Благодаря явлению самоиндукции это происходит постепенно. Конденсатор начинает перезаряжаться. Энергия магнитного поля преобразуется в энергию электрического поля.

 

 

t =0
Um - - - + + + I=0	- - + + I	Im U=0	- - - + + + I=0 Um - - + + I
Конденсатор разряжается. Сила тока увеличивается Электрическое поле превращается в магнитное поле.	Конденсатор перезаряжается. Сила тока уменьшается. Магнитное поле превращается в электрическое поле.

 

Если контур реальный, то потери энергии электромагнитного поля неизбежны, т. к. частично энергия электромагнитного поля переходит во внутреннюю энергию проводников, диэлектрика, а также выделяется в виде джоулевого тепла на активной нагрузке. В результате, в реальном контуре возникают свободные электромагнитные колебания, которые являются затухающими.

Вынужденные электромагнитные колебания

Переменный электрический ток представляет собой вынужденные ЭМК (являются незатухающими).

Для того чтобы колебания были незатухающими, на колеблющееся тело должна действовать внешняя периодически изменяющаяся сила.
Роль внешней силы выполняет Э. Д. С. от внешнего источника - генератора переменного тока, работающего на электростанции.

Вынужденные колебания электромагнитные обеспечивают работу электрических двигателей в станках на заводах и фабриках, приводят в действие электробытовые приборы и осветительные системы. Действие внешней переменной Э. Д. С. способно восстанавливать потерю энергии, создавать и поддерживать незатухающие электромагнитные колебания.

 

Характеристики электромагнитных колебаний:

Период – время, за которое происходит одно полное колебание.

- формула Томсона

Т – период колебаний [с]

L – индуктивность катушки[Гн]   C – электроёмкость конденсатора [Ф]

Т зависит от:

 

Частота – количество колебаний, происходящих за 1с.

– частота колебаний [Гц]

 

В России частота переменного тока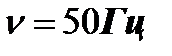

РЕЗОНАНС ТОКОВ

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с некоторой другой частотой, определяемой из параметров колебательной системы, таких как внутренняя (собственная) частота, коэффициент вязкости и т. п. Обычно резонансная частота не сильно отличается от собственной нормальной, но далеко не во всех случаях можно говорить об их совпадении.

В результате резонанса при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемойдобротностью. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Явление резонанса впервые было описано Галилео Галилеем в 1602 г. в работах, посвященных исследованиюмаятников и музыкальных струн

 

 

Резонанс токов, параллельный резонанс - получается в случае, когда генератор нагружен на индуктивность и емкость, соединенные параллельно, т.е. когда генератор включен вне контура (рис.1 а). Сам же колебательный контур, рассматриваемый отвлеченно от генератора, надо по-прежнему представлять себе как последовательную цепь из L и С. Не следует считать, что в схеме резонанса токов генератор и контур соединены между собой параллельно.

Весь контур в целом является нагрузочным сопротивлением для генератора и поэтому генератор

 

 

Рис.1 - Схема и резонансные кривые для резонанса токов

 

включен последовательно, как это и бывает всегда в замкнутой цепи.

Условия получения резонанса токов такие же, как и для резонанса напряжений: f = f₀ или x_L = х_C. Однако по своим свойствам резонанс токов во многом противоположен резонансу напряжений. В этом случае на катушке и на конденсаторе напряжение такое же, как у генератора. При резонансе сопротивление контура между точками разветвления становится максимальным, а ток генератора будет минимальным. Полное (эквивалентное) сопротивление контура для генератора при резонансе токов R_эможно подсчитать по любой из следующих формул

 

где L и С — в генри и фарадах, а R_э, р и r — в омах.

Сопротивление R_э, называемое резонансным сопротивлением, является чисто активным и поэтому при резонансе токов нет сдвига фаз между напряжением генератора и его током.

На (рис.1 б) для резонанса токов показано изменение полного сопротивления контура z и тока генератора I при изменении частоты генератора f.

В самом контуре при резонансе происходят сильные колебания и поэтому ток внутри контура во много раз больше, чем ток генератора. Токи в индуктивности и емкости I_L и I_С можно рассматривать как токи в ветвях или как ток незатухающих колебаний внутри контура, поддерживаемых генератором. По отношению к напряжению U ток в катушке отстает на 90°, а ток в емкости опережает это напряжение на 90°, т. е. друг относительно друга токи сдвинуты по фазе на 180°. Вследствие наличия активного сопротивления, сосредоточенного главным образом в катушке, токи I_L, и I_C в действительности имеют сдвиг фаз несколько меньше 180° и ток I_L немного( меньше I_C. Поэтому по первому закону Кирхгофа для точки разветвления можно написать

 

Чем меньше активное сопротивление в контуре, тем меньше разница между I_C и I_L, тем меньше ток генератора и тем больше сопротивление контура. Это вполне понятно. Ток, идущий от генератора, пополняет энергию в контуре, компенсируя потери ее в активном сопротивлении. При уменьшении активного сопротивления уменьшается потеря энергии в нем и генератор расходует меньше энергии на поддержание незатухающих колебаний.
Если бы контур был идеальным, то начавшиеся колебания продолжались бы непрерывно без затухания и не требовалось бы энергии от генератора на их поддержание. Ток генератора был бы равен нулю, а сопротивление контура — бесконечности.
Активная мощность, расходуемая генератором, может быть подсчитана как

 

или как мощность потерь в активном сопротивлении контура

где I_к — ток в контуре, равный I_L или I_C.

Для резонанса токов так же, как и для резонанса напряжений, характерно возникновение в контуре мощных колебаний при незначительной затрате мощности генератора.

На явление резонанса в параллельном контуре большое влияние оказывает внутреннее сопротивление R_i питающего генератора. Если это сопротивление мало, то напряжение на зажимах генератора, а следовательно, и на контуре незначительно отличается от эдс генератора и остается почти постоянным по амплитуде, несмотря на изменения тока при изменении частоты. Действительно, U = Е — IR_i, но так как R_i величина малая, то потеря напряжения внутри генератора IR_i также незначительна и U = Е.

Полное сопротивление цепи в этом случае приближенно равно только сопротивлению контура. При резонансе последнее сильно возрастает и ток генератора резко уменьшается. Кривая изменения тока на (рис.1 б) соответствует именно такому случаю.

Постоянство амплитуды напряжения на контуре также объясняет формула U = I * z. Для случая резонанса z велико, но I — величина малая, а если резонанса нет, то z уменьшается, но зато I увеличивается и произведение I*z остается примерно прежним.

Как видно, при малом Ri генератора параллельный контур не обладает резонансными свойствами в отношении напряжения: при резонансе напряжение на контуре почти не возрастает. Не будут заметно увеличиваться и токи IL И IС. Следовательно, при малом Ri генератора контур не имеет резонансных свойств и по отношению к токам в катушке и конденсаторе.

В радиотехнических схемах параллелыный контур обычно питается от генератора с большим внутренним сопротивлением, роль которого выполняет электронная лампа или полупроводниковый прибор. Если внутреннее сопротивление генератора значительно больше, чем сопротивление контура r, то параллельный контур приобретает резко выраженные резонансные свойства.

В этом случае полное сопротивление цепи приближенно равно одному Ri и почти неизменно при изменении частоты. Ток I, питающий контур, также почти постоянен по амплитуде:

 

 

Но тогда напряжение на контуре U = I * z при изменении частоты будет следовать за изменениями сопротивления контура z, т.е. при резонансе U резко увеличится. Соответственно возрастут токи I_L и I_C. Таким образом, при большом R_i генератора кривая изменения z (рис.1 б) будет в других масштабах приближенно показывать также изменение напряжения на контуре U и изменения токов I_L и I_C На (рис. 2) изображена подобная кривая вместе с графиком тока генератора, который в данном случае почти не меняется.

Рис.2 - Резонансные кривые параллельного контура при большом внутреннем сопротивлении генератора

Основное применение резонанса токов в радиотехнике — создание большого сопротивления для тока определенной частоты в ламповых генераторах и усилителях высокой частоты

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

- Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
- Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

- Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
- Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит .
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t1, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t1 = .
По истечении времени t1, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит .
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t2 = t1, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t1 и t2 составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t3, сменив полярность полюсов.

В течении заключительного этапа колебания (t4), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t1 + t2 + t3 + t4 составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfLравно реактивному сопротивлению ёмкости X_C=1/(2πfC).

 

 

8 Переменный электрический ток

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток.

Переменный электрический ток — это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

u=Um⋅sinωt или u=Um⋅cosωt ,

где u – мгновенное значение напряжения, U_m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

i=Im⋅sin(ωt+φc) ,

где φ_c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническомузакону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Генератор переменного тока

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.

Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

e=Em⋅sinω⋅t,

где Em=B⋅S⋅ω — амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R, через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке

i=eR=B⋅S⋅ωR⋅sinω⋅t=Im⋅sinω⋅t,

где Im=B⋅S⋅ωR — амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

индуктор — электромагнит или постоянный магнит, который создает магнитное поле;

якорь — обмотка, в которой индуцируется переменная ЭДС;

коллектор со щетками — устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

 

Рис. 1

Неподвижная часть генератора называется статором, а подвижная — ротором. В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.

На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы п