 |
Главная |
Проверка наличия тенденции
|
из
5.00
|
Лабораторная работа 1
«Анализ структуры ряда динамики»
Каждый студент согласно таблицы выбирает свой номер варианта и выполняет все лабораторные работы исходя из этих первоначальных данных.
| Начальная буква фамилии студента | № варианта | Начальная буква фамилии студента | № варианта | Начальная буква фамилии студента | № варианта |
| А, У | Г, Н, Ц | Ж, Р, Щ | |||
| Б, Л, Ф | Д, О, Ч, | З, С, Э | |||
| В, М, | Е, Ё, П | И, Т, Ю | |||
| Ш, Я | К, Х |
ТАБЛИЦА ИСХОДНЫХ ДАННЫХ
| № варианта месяц | произведено автомобилей, ты. шт. | уровень рождаемости, тыс. чел. | заработная плата, тыс. руб. | очередь в ДС, тыс. чел. | посещаемость студентов, чел. | численность заболевших гриппом, тыс. чел. | выручка, тыс. руб. | Урожайность грибов, кг | закуплено лекарств на сумму, тыс. руб. | выявлено правонарушений, шт. | посетило музеи, тыс. чел. |
Задание: В соответствии с вариантом задания, используя статистические данные, приведенные в таблице проанализировать структуру ряда динамики с использованием коэффициентов автокорреляции.
Наиболее простым и удобным методом анализа структуры ряда динамики является метод, основанный на расчете линейного коэффициента автокорреляции (по аналогии с коэффициентом корреляции при анализе пространственных данных) между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на несколько шагов во времени. Сдвиг временного ряда во времени называется лагом (L). При этом, если L = 1, то коэффициент автокорреляции называется коэффициентом автокорреляции первого порядка r(1), если L = 2, - второго порядка r(2) и. т. д. На практике рекомендуется максимальный порядок коэффициента автокорреляции принимать равным n/4. Где n – число наблюдений ряда динамики. Коэффициент автокорреляции определяется по зависимости
 , (1)
, (1)
где  ;
;
 - средний уровень ряда (y1+L, y2+L, …, yn);
- средний уровень ряда (y1+L, y2+L, …, yn);
 средний уровень ряда (y1, y2, …, yn-L);
средний уровень ряда (y1, y2, …, yn-L);
St, St-L – среднеквадратические отклонения для рядов (y1+L, y2+L, …, yn) и (y1, y2, …, yn-L) соответственно.
Возможности табличного процессора MS Excel позволяют достаточно просто рассчитать коэффициент автокорреляции с помощью инструмента Корреляция надстройки Пакет анализа. Выполним расчеты на примере исходных данных приведенных в таблице 1.
Таблица 1 - Среднедушевые денежные доходы населения условного региона
| Месяц | Среднедушевые денежные доходы, руб. | Временной лаг L=1 | Временной лаг L=2 | Временной лаг L=3 |
| Январь | 476,0 | |||
| Февраль | 544,0 | 476,0 | ||
| Март | 651,0 | 544,0 | 476,0 | |
| Апрель | 680,0 | 651,0 | 544,0 | 476,0 |
| Май | 631,0 | 680,0 | 651,0 | 544,0 |
| Июнь | 663,0 | 631,0 | 680,0 | 651,0 |
| Июль | 705,0 | 663,0 | 631,0 | 680,0 |
| Август | 761,0 | 705,0 | 663,0 | 631,0 |
| Сентябрь | 712,0 | 761,0 | 705,0 | 663,0 |
| Октябрь | 772,0 | 712,0 | 761,0 | 705,0 |
| Ноябрь | 876,0 | 772,0 | 712,0 | 761,0 |
| Декабрь | 1258,0 | 876,0 | 772,0 | 712,0 |
Алгоритм расчета коэффициента автокорреляции.
1. Выбрать команду Сервис Þ Надстройки.
2. В появившемся диалоговом окне Надстройки (рисунок 2) установить флажок Пакет анализа.
3. Щелкнуть по кнопке ОК.
4. Из главного меню выбрать команду Сервис Þ Анализ данных
5. Выбрать из списка (рисунок 3) инструмент анализа Корреляция.
6. Щелкнуть по кнопке ОК. Появиться диалоговое окно Корреляция (рисунок 4).
7. В поле Выходной интервал необходимо ввести исходные данные в соответствии с таблицей 1.
8. Задать ячейку для Выходного интервала и щелкнуть по кнопке ОК.
9. Результаты расчета коэффициентов автокорреляции приведены на рисунке 5.
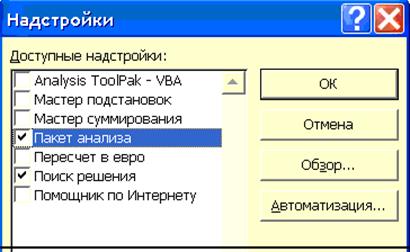
Рисунок 2 - Диалоговое окно Надстройки

Рисунок 3 - Диалоговое окно Анализ данных

Рисунок 4 - Диалоговое окно Корреляция
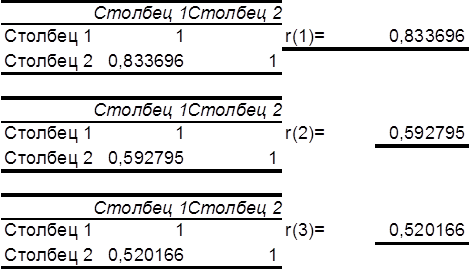
Рисунок 5 - Результаты расчета
На практике установлено, что, если наибольшим оказался коэффициент автокорреляции первого порядка (а это именно рассматриваемый пример), то исследуемый ряд динамики содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка L, то ряд, помимо тенденции, содержит колебания с периодом L. Если ни один из коэффициентов автокорреляции не является существенно значимым, то можно сделать два предположения:
- либо ряд не содержит тенденции и колебаний, а его уровни определяются только случайной компонентой;
- либо ряд содержит сильную нелинейную тенденцию, для выявления которой необходимо провести дополнительные исследования.
Лабораторная работа 2
Проверка наличия тенденции
Задание: В соответствии с вариантом задания, используя статистические данные, приведенные в таблице определите наличие тенденции в ряду динамики.
В настоящий момент существует более десятка критериев проверки наличия тенденции (тренда). Наиболее распространенными из них являются.
1. Критерий, связанный с проверкой существенности разности средних.
2. Критерий, определяемый по методу Фостера–Стюарта.
При реализации критерия существенности разности средних ряд динамики разбивается на две равные или почти равные части. Проверяется гипотеза о существовании разности средних:
Н0:  .
.
Так как число членов анализируемого ряда, как правило, мало, то для проверки гипотезы воспользуемся теорией малой выборки. За основу проверки берется t – критерий Стьюдента, который используется при проверке статистических гипотез при небольшом объёме выборки (при этом f (число степеней свободы) и n (количество опытов) различается на f=n-1).
В случае равенства или при несущественном различии дисперсий двух исследуемых совокупностей (  =
=  ) определение расчетного значения критерия Стьюдента tр производится по зависимости
) определение расчетного значения критерия Стьюдента tр производится по зависимости
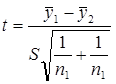 , (1)
, (1)
где  и
и 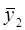 средние для первой и второй половины ряда динамики;
средние для первой и второй половины ряда динамики;
n1 и n2 - число уровней в первой и второй половине ряда;
S – среднеквадратическое отклонение разности средних, определяемое по зависимости
 . (2)
. (2)
Дисперсии для первой и второй половин ряда рассчитываются по зависимости
 . ( 3 )
. ( 3 )
Проверка гипотезы о равенстве дисперсий осуществляется с помощью F-критерия, основанного на сравнении расчетного отношения с табличным. Расчетное значение критерия определяется по формуле
 , (4 )
, (4 )
Если расчетное значение F меньше табличного, при заданном уровне значимости, то гипотеза о равенстве дисперсий принимается. Если Fр больше, чем табличное значение, то гипотеза о равенстве дисперсий отклоняется, и зависимость для расчета t не пригодна для использования.
При выполнении условия о равенстве дисперсий определяется значение tр и проверяется гипотеза (Н0). При этом критическое значение критерия Стьюдента tкрит. определяется с числом степеней свободы, равным n1 +n2–2
Пример.
Используя данные, приведенные в таблице 1 определить наличие тенденции в ряду динамики среднедушевых денежных доходов населения.
Решение.
1. Исходный ряд разбиваем на две равные части ( по шесть месяцев).
2. Используя инструмент Двухвыборочный F-тест для дисперсии надстройки Пакет анализа табличного процессора MS Excelпроверяем гипотезу о равенстве дисперсий с помощью F-критерия

Рисунок 6- Диалоговое окно выбора инструмента инструмент Двухвыборочный F-тест для дисперсии

Рисунок 7- Окно диалога Двухвыборочный F-тест для дисперсии
Результаты тестирования представлены на рисунке 8.

Рисунок 8-Резульаты тестирования
Из рисунка 8 видно, что, что расчетное значение F –критерия (0, 145161217) меньше табличного (критического) (0,198006944) следовательно, гипотеза о равенстве дисперсий принимается, что является основанием для применения t – критерий Стьюдента при проверке существенности разности средних
Н0:  .
.
3. Используя инструмент ПарныйДвухвыборочный t-тест для средних надстройки Пакет анализа табличного процессора MS Excelпроверяем гипотезу о равенстве средних с помощью t-критерия

Рисунок 9- Диалоговое окно выбора инструмента ПарныйДвухвыборочный t-тест для средних
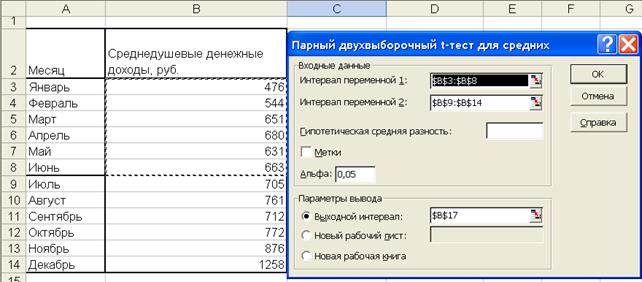
Рисунок 10-Окно диалога ПарныйДвухвыборочный t-тест для средних
Результаты тестирования представлены на рисунке 11.

Рисунок 11-Резульаты тестирования
Из рисунка 11 видно, что, что расчетное значение t –критерия (-3,090703889) больше табличного (критического) (2,015049176) следовательно, нулевая гипотеза о равенстве средних отвергается и принимается альтернативная ей гипотеза H1
 ,
,
и в ряду динамики наблюдается тенденция.
В заключение следует отметить, что изложенный выше метод дает положительные результаты для рядов с монотонной тенденцией. Когда же ряд динамики меняет общее направление развития, то точка поворота тенденции оказывается близкой к середине ряда. Поэтому средние двух отрезков будут близки, а проверка может не показать наличие тенденции.
Лабораторная работа 3
|
из
5.00
|
Обсуждение в статье: Проверка наличия тенденции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

