 |
Главная |
Функциональные характеристики стационарных систем обслуживания
|
из
5.00
|
Основными функциональными характеристиками СМО являются следующие.
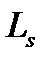 -среднее число находящихся в системе клиентов,
-среднее число находящихся в системе клиентов,
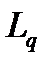 -среднее число клиентов в очереди,
-среднее число клиентов в очереди,
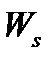 -средняя продолжительность пребывания клиента в системе,
-средняя продолжительность пребывания клиента в системе,
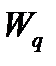 -средняя продолжительность пребывания клиента в очереди,
-средняя продолжительность пребывания клиента в очереди,
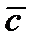 -среднее количество занятых средств обслуживания (сервисов).
-среднее количество занятых средств обслуживания (сервисов).
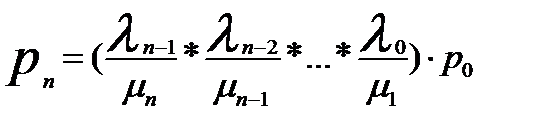 (7)
(7)
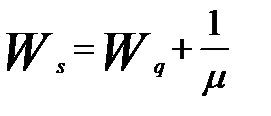 (8)
(8)
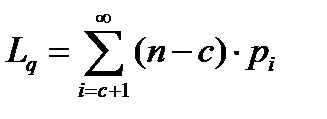 (9)
(9)
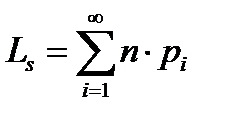 (10)
(10)
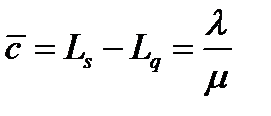 (11)
(11)
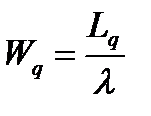 (12)
(12)
Глава 3. Анализ статистических данных о поступлении заявок на получение кредита по дням недели и в течение дня по часам.
Проверим при уровне значимости 0,95 гипотезу о том, что время поступления заявок в систему распределено экспоненциально на примере одного дня.
На основе начальных данных (время поступления заявок) посчитаем время между приходом заявок.
| № п/п | Дата поступления заявки | Время поступления заявки (час) | Время между заявками |
| 22.05.2014 | 10:08 | 0:06 | |
| 22.05.2014 | 10:14 | 0:14 | |
| 22.05.2014 | 10:28 | 0:03 | |
| 22.05.2014 | 10:31 | 0:02 | |
| 22.05.2014 | 10:33 | 0:03 | |
| 22.05.2014 | 10:36 | 0:10 | |
| 22.05.2014 | 10:46 | 0:03 | |
| 22.05.2014 | 10:49 | 0:02 | |
| 22.05.2014 | 10:51 | 0:05 | |
| 22.05.2014 | 10:56 | 0:10 | |
| 22.05.2014 | 11:06 | 0:04 | |
| 22.05.2014 | 11:10 | 0:31 | |
| 22.05.2014 | 11:41 | 0:00 | |
| 22.05.2014 | 11:41 | 0:09 | |
| 22.05.2014 | 11:50 | 0:03 | |
| 22.05.2014 | 11:53 | 0:12 | |
| 22.05.2014 | 12:05 | 0:04 | |
| 22.05.2014 | 12:09 | 0:15 | |
| 22.05.2014 | 12:24 | 0:09 | |
| 22.05.2014 | 12:33 | 0:01 | |
| 22.05.2014 | 12:34 | 0:00 | |
| 22.05.2014 | 12:34 | 0:24 | |
| 22.05.2014 | 12:58 | 0:08 | |
| 22.05.2014 | 13:06 | 0:00 | |
| 22.05.2014 | 13:06 | 0:20 | |
| 22.05.2014 | 13:26 | 0:07 | |
| 22.05.2014 | 13:33 | 0:03 | |
| 22.05.2014 | 13:36 | 0:11 | |
| 22.05.2014 | 13:47 | 0:03 | |
| 22.05.2014 | 13:50 | 0:05 | |
| 22.05.2014 | 13:55 | 0:01 | |
| 22.05.2014 | 13:56 | 0:06 | |
| 22.05.2014 | 14:02 | 0:09 | |
| 22.05.2014 | 14:11 | 0:37 | |
| 22.05.2014 | 14:48 | 0:03 | |
| 22.05.2014 | 14:51 | 0:13 | |
| 22.05.2014 | 15:04 | 0:17 | |
| 22.05.2014 | 15:21 | 0:17 | |
| 22.05.2014 | 15:38 | 0:36 | |
| 22.05.2014 | 16:14 | 0:15 | |
| 22.05.2014 | 16:29 | 0:01 | |
| 22.05.2014 | 16:30 | 0:02 | |
| 22.05.2014 | 16:32 |
Таблица 1
Найдем шаг h для деления времени между поступлениями на частичные интервалы, который находится по формуле Стерджесса
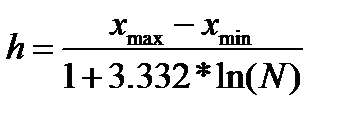 (13)
(13)
Где 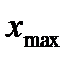 - максимальное и
- максимальное и 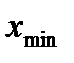 - минимальное время между поступлениями, а N – число заявок поступивших за день.
- минимальное время между поступлениями, а N – число заявок поступивших за день.
| Максимум = 37 | |
| Минимум = 0 | |
| h = 2,75779 | |
| N = 42 |
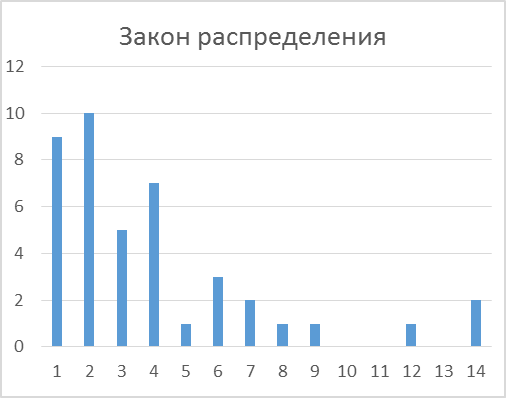 Разделим отрезок [0,37] на частичные интервалы с шагом h и прочитаем частоту попадания времени между приходами заявок в частичные интервалы. Так же мы построим гистограмму.
Разделим отрезок [0,37] на частичные интервалы с шагом h и прочитаем частоту попадания времени между приходами заявок в частичные интервалы. Так же мы построим гистограмму.
| Гистограмма 1 |
Таблица 2
По гистограмме видно, что скорее всего это экспоненциальное распределение. Мы знаем, что для экспоненциального распределения параметр 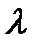 равен:
равен:
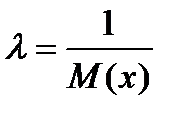 или
или 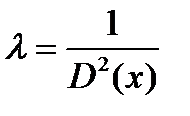 (15)
(15)
Далее посчитаем выборочное среднее и выборочную дисперсию и с помощью критерия Пирсона проверим гипотезу об экспоненциальном распределении.
| F(i) | M(i) | M(i)*F(i) | M(i)^2*F(i) |
| Частоты | Середины интервалов | Параметры распределения | |
| 1,378895163 | 12,41005646 | 17,11217 | |
| 4,136685488 | 41,36685488 | 171,1217 | |
| 6,894475814 | 34,47237907 | 237,669 | |
| 9,652266139 | 67,56586298 | 652,1637 | |
| 12,41005646 | 12,41005646 | 154,0095 | |
| 15,16784679 | 45,50354037 | 690,1907 | |
| 17,92563712 | 35,85127423 | 642,6569 | |
| 20,68342744 | 20,68342744 | 427,8042 | |
| 23,44121777 | 23,44121777 | 549,4907 | |
| 26,19900809 | |||
| 28,95679842 | |||
| 31,71458874 | 31,71458874 | 1005,815 | |
| 34,47237907 | |||
| 37,23016939 | 74,46033879 | 2772,171 |
Таблица 3
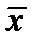 = 9,520942791
= 9,520942791
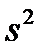 = 85,682291
= 85,682291
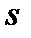 = 9,256472924
= 9,256472924
Так как среднее выборочное и корень из выборочной дисперсии не равны, но довольно близки, то
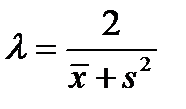 (16)
(16)
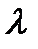 = 0,106510929
= 0,106510929
Посчитаем теоретические частоты с использованием экспоненциального распределения с параметром 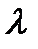 .
.
| Вероятность попадания | Число попаданий | ||
| 0,254525843 | 10,690085 | 0,363636 | |
| 0,189742438 | 7,9691824 | 0,5 | |
| 0,141448084 | 5,9408195 | 0,166667 | |
| 0,105445891 | 4,4287274 | 0,142857 | |
| 0,078607187 | 3,3015019 | 0,5 | |
| 0,058599626 | 2,4611843 | ||
| 0,043684507 | 1,8347493 | ||
| 0,032565671 | 1,3677582 | ||
| 0,024276866 | 1,0196284 | ||
| 0,018097776 | 0,7601066 | ||
| 0,013491425 | 0,5666398 | ||
| 0,010057508 | 0,4224154 | ||
| 0,007497613 | 0,3148997 | ||
| 0,005589276 | 0,2347496 | ||
| 0,016370287 | 0,6875521 | ||
| Значение критерия Пирсона: | 1,67316 |
Таблица 4
Сравним с критическим значением с уровнем доверия 0,95 и 3-мя степенями свободы.
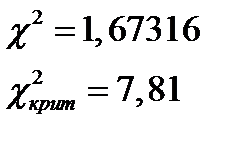
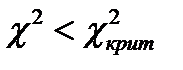 следовательно мы принимаем гипотезу о том, что распределение носит экспоненциальный характер с параметром
следовательно мы принимаем гипотезу о том, что распределение носит экспоненциальный характер с параметром 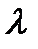 = 0,106510929.
= 0,106510929.
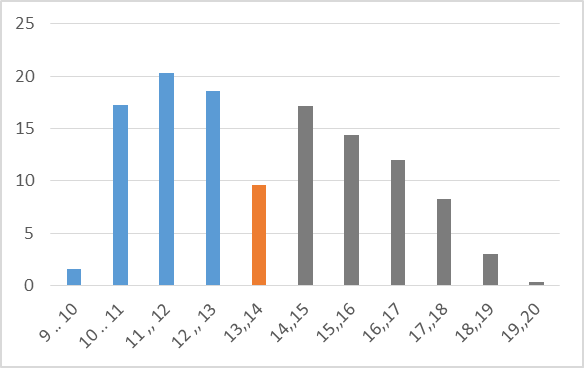 Рассмотрим по часам среднюю частоту прихода посетителей за неделю и построим гистограмму.
Рассмотрим по часам среднюю частоту прихода посетителей за неделю и построим гистограмму.
| Гистограмма 2 | |||||||||||||||||||||||||||
| Таблица 5 |
Из гистограммы явно видно, что по частоте прихода день делится на три части:
1. С 9 до 13 – пик активности;
2. С 13 до 14 – спад;
3. С 14 до 20 – второй пик.
|
из
5.00
|
Обсуждение в статье: Функциональные характеристики стационарных систем обслуживания |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

