 |
Главная |
Глава 4. Построение имитационной модели
|
из
5.00
|
Для имитирования возьмем второй день рабочей недели (вторник). По нашим расчетам среднее выборочное для него равно 3,6.
Описание модели
·заявки на получение кредита поступают независимо друг от друга с в среднем каждые 3,6 минуты, образуя входящий поток;
· заявки обслуживаются четырьмя диспетчерами;
· если при поступлении заявки диспетчер свободен, то заявка мгновенно поступает на обслуживание;
·заявка обслуживается в среднем 15 минут;
· обслуженные заявки покидают систему
Алгоритм
1. С помощью нармально распределенной на отрезке [0,1] случайной величины разыгрываем, в какую часть дня придет заявка.
2. Отсортировав данные по частям дня, разыгрываем помощью нармально распределенной на отрезке [0,1] случайную величину и по закону Пуассона определяем время прихода заявки.
3. Рассчитываем время покидание заявкой системы и количество человек в очереди на этот момент.
4. Определяем параметры системы.
| N | R | R | Т прихода | Т ухода | Т очереди | Длинна очереди | ||
| 0,452219 | 0,171847 | 9,606 | 9,856 | |||||
| 0,348361 | 0,185406 | 9,707 | 9,957 | |||||
| 0,298692 | 0,374542 | 9,766 | 10,016 | |||||
| 0,041385 | 0,878264 | 9,773 | 10,023 | |||||
| 0,011037 | 0,09258 | 9,916 | 10,166 | 0,00 | ||||
| 0,38688 | 0,182492 | 10,018 | 10,268 | 0,00 | ||||
| 0,006519 | 0,49215 | 10,061 | 10,311 | 0,00 | ||||
| 0,453486 | 0,378121 | 10,119 | 10,369 | 0,00 | ||||
| 0,448703 | 0,705367 | 10,140 | 10,416 | 0,03 | ||||
| 0,326659 | 0,285998 | 10,215 | 10,518 | 0,05 | ||||
| 0,01338 | 0,418919 | 10,267 | 10,561 | 0,04 | ||||
| 0,13249 | 0,349609 | 10,331 | 10,619 | 0,04 | ||||
| 0,275898 | 0,564533 | 10,365 | 10,666 | 0,05 | ||||
| 0,140831 | 0,481711 | 10,409 | 10,768 | 0,11 | ||||
| 0,218581 | 0,599153 | 10,439 | 10,811 | 0,12 | ||||
| 0,265246 | 0,370508 | 10,499 | 10,869 | 0,12 | ||||
| 0,425015 | 0,816953 | 10,511 | 10,916 | 0,16 | ||||
| 0,016981 | 0,389979 | 10,568 | 11,018 | 0,20 | ||||
| 0,215585 | 0,839698 | 10,578 | 11,061 | 0,23 | ||||
| 0,44085 | 0,511142 | 10,618 | 11,119 | 0,25 | ||||
| 0,128578 | 0,460896 | 10,665 | 11,166 | 0,25 | ||||
| 0,138548 | 0,766229 | 10,681 | 11,268 | 0,34 | ||||
| 0,065255 | 0,078416 | 10,834 | 11,311 | 0,23 | ||||
| 0,411271 | 0,105866 | 10,968 | 11,369 | 0,15 | ||||
| 0,424819 | 0,26804 | 11,047 | 11,416 | 0,12 | ||||
| 0,107676 | 0,829073 | 11,059 | 11,518 | 0,21 | ||||
| 0,384552 | 0,306262 | 11,130 | 11,561 | 0,18 | ||||
| 0,151041 | 0,175461 | 11,234 | 11,619 | 0,14 | ||||
| 0,11307 | 0,814473 | 11,246 | 11,666 | 0,17 | ||||
| 0,166133 | 0,558017 | 11,281 | 11,768 | 0,24 | ||||
| 0,012748 | 0,708088 | 11,302 | 11,811 | 0,26 | ||||
| 0,30765 | 0,1427 | 11,419 | 11,869 | 0,20 | ||||
| 0,353121 | 0,02864 | 11,632 | 11,916 | 0,03 | ||||
| 0,377585 | 0,419117 | 11,684 | 12,018 | 0,08 | ||||
| 0,09014 | 0,393823 | 11,740 | 12,061 | 0,07 | ||||
| 0,192277 | 0,671851 | 11,764 | 12,119 | 0,11 | ||||
| 0,412926 | 0,367932 | 11,824 | 12,166 | 0,09 | ||||
| 0,395797 | 0,229202 | 11,912 | 12,268 | 0,11 | ||||
| 0,24727 | 0,565529 | 11,947 | 12,311 | 0,11 | ||||
| 0,288002 | 0,145809 | 12,062 | 12,369 | 0,06 | ||||
| 0,051769 | 0,705572 | 12,083 | 12,416 | 0,08 | ||||
| 0,099739 | 0,865759 | 12,092 | 12,518 | 0,18 | ||||
| 0,185842 | 0,4258 | 12,143 | 12,561 | 0,17 | ||||
| 0,244085 | 0,047766 | 12,325 | 12,619 | 0,04 | ||||
| 0,059555 | 0,323853 | 12,393 | 12,666 | 0,02 | ||||
| 0,098077 | 0,674369 | 12,417 | 12,768 | 0,10 | ||||
| 0,118427 | 0,434064 | 12,467 | 12,811 | 0,09 | ||||
| 0,410436 | 0,796356 | 12,480 | 12,869 | 0,14 | ||||
| 0,036813 | 0,885944 | 12,488 | 12,916 | 0,18 | ||||
| 0,27896 | 0,793083 | 12,502 | 13,018 | 0,27 | ||||
| 0,2898 | 0,276185 | 12,579 | 13,061 | 0,23 | ||||
| 0,467204 | 0,535607 | 13,037 | 13,287 | 0,00 | ||||
| 0,467435 | 0,671463 | 13,061 | 13,311 | 0,00 | ||||
| 0,482379 | 0,985666 | 13,062 | 13,312 | 0,00 | ||||
| 0,482174 | 0,251386 | 13,145 | 13,395 | 0,00 | ||||
| 0,518246 | 0,144783 | 13,261 | 13,537 | 0,03 | ||||
| 0,486399 | 0,960769 | 13,263 | 13,561 | 0,05 | ||||
| 0,49469 | 0,769619 | 13,279 | 13,562 | 0,03 | ||||
| 0,505225 | 0,157753 | 13,390 | 13,645 | 0,01 | ||||
| 0,476592 | 0,566152 | 13,424 | 13,787 | 0,11 | ||||
| 0,5463 | 0,151654 | 14,113 | 14,363 | 0,00 | ||||
| 0,980895 | 0,922785 | 14,118 | 14,368 | 0,00 | ||||
| 0,822593 | 0,657393 | 14,143 | 14,393 | 0,00 | ||||
| 0,787618 | 0,702293 | 14,164 | 14,414 | 0,00 | ||||
| 0,619285 | 0,179559 | 14,267 | 14,613 | 0,10 | ||||
| 0,725709 | 0,278441 | 14,344 | 14,618 | 0,02 | ||||
| 0,688254 | 0,476797 | 14,389 | 14,643 | 0,00 | ||||
| 0,840544 | 0,571743 | 14,422 | 14,672 | 0,00 | ||||
| 0,697154 | 0,389755 | 14,479 | 14,863 | 0,13 | ||||
| 0,934605 | 0,342624 | 14,543 | 14,868 | 0,08 | ||||
| 0,665688 | 0,84923 | 14,553 | 14,893 | 0,09 | ||||
| 0,768891 | 0,543324 | 14,589 | 14,922 | 0,08 | ||||
| 0,650094 | 0,634588 | 14,617 | 15,113 | 0,25 | ||||
| 0,906799 | 0,320975 | 14,685 | 15,118 | 0,18 | ||||
| 0,969092 | 0,905944 | 14,691 | 15,143 | 0,20 | ||||
| 0,819603 | 0,934825 | 14,695 | 15,172 | 0,23 | ||||
| 0,783539 | 0,641542 | 14,721 | 15,363 | 0,39 | ||||
| 0,634746 | 0,846203 | 14,731 | 15,368 | 0,39 | ||||
| 0,718226 | 0,386675 | 14,788 | 15,393 | 0,35 | ||||
| 0,581192 | 0,675525 | 14,812 | 15,422 | 0,36 | ||||
| 0,931362 | 0,921709 | 14,817 | 15,613 | 0,55 | ||||
| 0,665182 | 0,772689 | 14,832 | 15,618 | 0,54 | ||||
| 0,586234 | 0,3387 | 14,897 | 15,643 | 0,50 | ||||
| 0,822063 | 0,56139 | 14,932 | 15,672 | 0,49 | ||||
| 0,965164 | 0,821185 | 14,944 | 15,863 | 0,67 | ||||
| 0,760775 | 0,149209 | 15,058 | 15,868 | 0,56 | ||||
| 0,601653 | 0,941656 | 15,061 | 15,893 | 0,58 | ||||
| 0,593167 | 0,734762 | 15,080 | 15,922 | 0,59 | ||||
| 0,930298 | 0,59301 | 15,111 | 16,113 | 0,75 | ||||
| 0,82207 | 0,093807 | 15,253 | 16,118 | 0,61 | ||||
| 0,820902 | 0,169005 | 15,360 | 16,143 | 0,53 | ||||
| 0,847392 | 0,34525 | 15,424 | 16,172 | 0,50 | ||||
| 0,844566 | 0,717102 | 15,444 | 16,363 | 0,67 | ||||
| 0,892431 | 0,130864 | 15,566 | 16,368 | 0,55 | ||||
| 0,829696 | 0,095399 | 15,707 | 16,393 | 0,44 | ||||
| 0,644512 | 0,622035 | 15,735 | 16,422 | 0,44 | ||||
| 0,967474 | 0,478519 | 15,779 | 16,613 | 0,58 | ||||
| 0,847292 | 0,017143 | 16,023 | 16,618 | 0,34 | ||||
| 0,675415 | 0,371713 | 16,083 | 16,643 | 0,31 | ||||
| 0,829157 | 0,566167 | 16,117 | 16,672 | 0,31 | ||||
| 0,569715 | 0,62487 | 16,145 | 16,863 | 0,47 | ||||
| 0,808567 | 0,206881 | 16,240 | 16,868 | 0,38 | ||||
| 0,655252 | 0,558601 | 16,275 | 16,893 | 0,37 | ||||
| 0,608154 | 0,187594 | 16,375 | 16,922 | 0,30 | ||||
| 0,930013 | 0,831682 | 16,386 | 17,113 | 0,48 | ||||
| 0,66357 | 0,841855 | 16,396 | 17,118 | 0,47 | ||||
| 0,974247 | 0,36079 | 16,458 | 17,143 | 0,44 | ||||
| 0,687711 | 0,770578 | 16,473 | 17,172 | 0,45 | ||||
| 0,56973 | 0,394289 | 16,529 | 17,363 | 0,58 | ||||
| 0,78273 | 0,232463 | 16,617 | 17,368 | 0,50 | ||||
| 0,814565 | 0,425637 | 16,668 | 17,393 | 0,48 | ||||
| 0,78513 | 0,523227 | 16,707 | 17,422 | 0,47 |
Таблица 6
1. Время имитации – 7,9 часа;
2. Средняя длинна очереди – 3,2 заявки;
3. Средняя занятость системы – 3,7 кассы;
4. Среднее время ожидания в очереди – 13,4 минуты.
5. Среднее время нахождения в системе – 28,4 минуты;
6. Среднее число заявок в системе – 7,2 заявки.
Расчет характеристик СМО
Рассчитаем основные функциональные характеристики СМО:
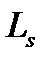 -среднее число находящихся в системе заявок,
-среднее число находящихся в системе заявок,
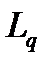 -среднее число заявок в очереди,
-среднее число заявок в очереди,
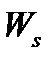 -средняя продолжительность пребывания заявка в системе,
-средняя продолжительность пребывания заявка в системе,
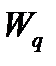 -средняя продолжительность пребывания заявки в очереди,
-средняя продолжительность пребывания заявки в очереди,
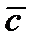 -среднее количество занятых средств обслуживания (касс).
-среднее количество занятых средств обслуживания (касс).
Для расчетов возьмем среднее значение выборочного среднего за семь дней.
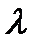 =
= 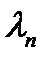 =60/5=12 заявок в час
=60/5=12 заявок в час
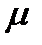 =4
=4
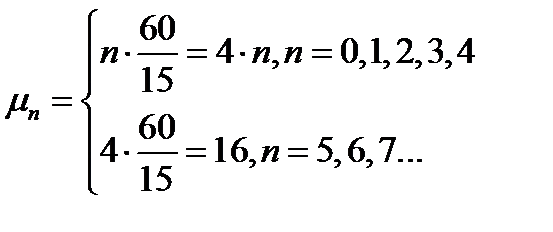 (17)
(17)
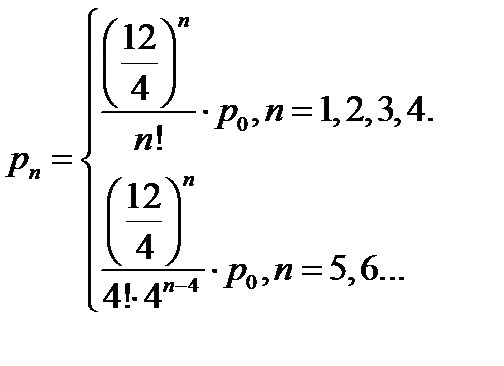 (18)
(18)
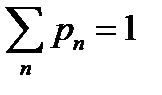 (19)
(19)
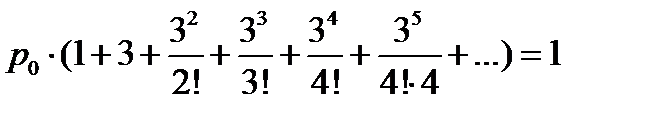 (20)
(20)
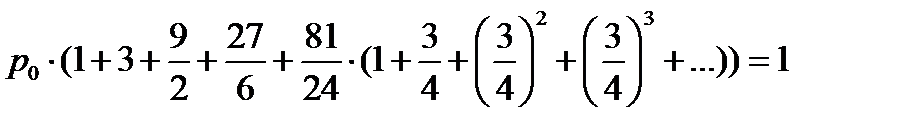 (21)
(21)
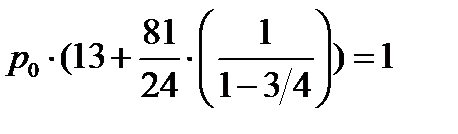 (22)
(22)
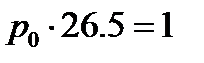
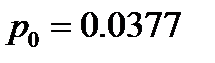
| n | ||||

| 0.1131 | 0.16965 | 0.16965 | 0.1272 |
Таблица 7
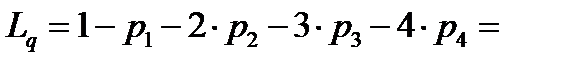 1.8 заявки.
1.8 заявки.
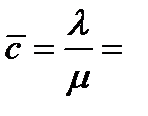 3 кассы.
3 кассы.
 заявки.
заявки.
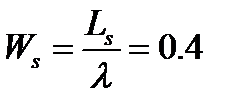 часа.
часа.
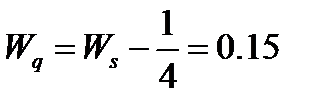 часа.
часа.
Выводы
Основные функциональные характеристики СМО для средней интенсивности входного потока за неделю оказались лучше, чем характеристики полученные при моделировании одного дня (вторника).
Это говорит о том, что интенсивность поступления заявок в течении недели не равномерна. Во вторник частота поступления заявок выше, чем в среднем за неделю (на 3 заявки в час), что приводит к повышенной нагрузке на кассы и созданию очередей.
В модельный день среднее время нахождения заявки в очереди возрастает на 4,4 минуты, средняя длина очереди – в 2 раза, а средняя занятость системы на 0,7 кассы.
Заключение
Мы показали, что наша СМО имеет пуассоновский входной поток (или экспоненциальное распределение между моментами последовательных поступлений клиентов).
Мы построили имитационную модель одного дня и посчитали:
1. Среднюю продолжительность пребывания заявки в системе;
2. Среднюю продолжительность пребывания заявки в очереди;
3. Среднее число заявок в очереди;
4. Среднее количество занятых средств обслуживания (касс).
Рассчитали основные функциональные характеристики СМО для средней интенсивности входного потока за неделю:
1. 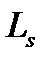 -среднее число находящихся в системе заявок,
-среднее число находящихся в системе заявок,
2. 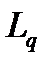 -среднее число заявок в очереди,
-среднее число заявок в очереди,
3. 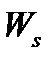 -средняя продолжительность пребывания заявка в системе,
-средняя продолжительность пребывания заявка в системе,
4. 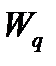 -средняя продолжительность пребывания заявки в очереди,
-средняя продолжительность пребывания заявки в очереди,
5. 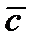 -среднее количество занятых средств обслуживания (касс).
-среднее количество занятых средств обслуживания (касс).
Список литературы
1. Имитационное моделирование: учебное пособие / В.В.Мешечкин, М.В.Косенкова; Кемеровский государственный университет. – Кемерово, 2012. -116 стр
2. Руководство к решению задач по теории вероятностей и математической статистике / В.Е.Гмурман; Высш. Школа,1979, 400 стр.
3. Введение в исследование операций. 6-е издание. / Хемди А. Таха; Издательский дом «Вильямс», 2001 – 912 стр.
4. Имитационное моделирование систем – Искусство и Наука. / Р.Шеннон; издательство «Мир» Москва, 1978 – 421 стр.
|
из
5.00
|
Обсуждение в статье: Глава 4. Построение имитационной модели |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

