Структурный синтез механизма без избыточных связей

Динамическое исследование

Структурный анализ исполнительного механизма

Механизм грохота (рисунок 1) состоит из пяти звеньев: 1 – кривошипа ОА, совершающего вращательное движение; 2 – ползуна А, совершающего возвратно-поступательное движение по кулисе; 3 – коромысла АВС, совершающего качательное движение вокруг шарнира В; 4 – шатуна СD; 5 – ползуна D, совершающего возвратно-поступательное движение; а также семи кинематических пар.

Рис.1. Схема кривошипно–ползунного механизма грохота:

: 1 – кривошип, 2 – ползун, 3 – коромысла, 4 – шатун, 5 – ползуна

Где n – число подвижных звеньев для механизма, n =5;

Р₅ – число кинематических пар V класса, Р₅ = 7;

Р₄ – число кинематических пар IV класса, Р₄ = 0.

Разбивка механизма на структурные группы

Согласно классификации И. И. Артоболевского разобьем исследуемый механизм на структурные группы. Механизм грохота (рисунок 1) состоит из ведущего звена 1 и двух структурных групп II класса 2 порядка.

Обе структурные группы относятся к третьему виду: первая – (звенья 2 и 3), и вторая – (звенья 4 и 5). Структурные группы состоят из 2 звеньев и 3 кинематических пар. Формула строения механизма имеет вид:

Рис.2. Исполнительный механизм грохота

Число избыточных связей q для плоской схемы определим с помощью формулы Чебышева-Малышева:

W_n - q_n = 3n - 2p_1n - p_2n

q_n = -3·5 - 2·7 - 0

q_n = 1

Число избыточных связей q для пространственной схемы определим с помощью формулы Сомова-Малышева:

n=5

p₁=7

p₄=0

W - q = 6n - 5p₁ - 4p₂ - 3p₃ - 2p₄ - p₅

q = W - 6n + 5p₁ + 2p₄

q = 1-6·5+5·7+2·0

q = 6

В пространственной схеме механизма имеется 6 избыточные связи, поэтому его сборка будет происходить с натягами за счет деформации звеньев.

Разделим механизм на группы Ассура:

I₁ (0;1) II₃ (2;3) ВПВ

II₂ (4;5) ВВП

Формула строения механизма:

М = I₁ (1;0) + II₃ (2;6) + II₂ (3;4)

Механизм второго класса, так как наивысший класс группы равен II.

Структурный синтез механизма без избыточных связей

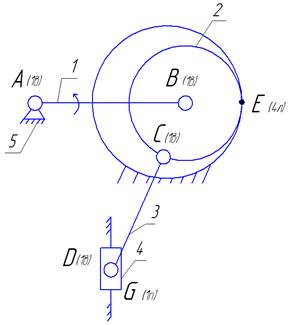
Рис.4. Схема исполнительного механизма зубчато-рычажного пресса

n=4

p₁=5

p₄=1

Число избыточных связей q для пространственной схемы:

W - q = 6n - 5p₁ - 4p₂ - 3p₃ - 2p₄ - p₅

q = W - 6n + 5p₁ + 2p₄

q = 1-6·4+5·5+2·1

q = 4

Число замкнутых контуров определим по формуле Гофмана:

k = p_∑ - n = 6 - 4 = 2

В схеме исполнительного механизма зубчато-рычажного пресса два замкнутых контура: ABCDG с одноподвижными парами и контур ABE, в составе которого есть высшая кинематическая пара зубчатого зацепления.

Рассмотрим контур ABCDG, он содержит 3 избыточные связи. Для самоустанавливаемости звеньев заменим одноподвижные вращательные пары в шарнирах С и D, на двухподвижную цилиндрическую и трехподвижную сферическую пары соответственно.

Рис.5. Сборка контура ABCDG

Рассмотрим контур ABE, высшая кинематическая пара вносит в цепь еще одну лишнюю избыточную связь. В точке Е происходит соединение двух зубчатых колес, таким образом замена четырехподвижной линейной высшей кинематической пары на пятиподвижную с точечным контактом весьма не целесообразна, так как потребуется изготовление зубчатых колес с повышенной точностью.

Рис.6. Схема исполнительного механизма зубчато-рычажного пресса без избыточных связей