 |
Главная |
Точечные оценки и требования к ним
|
из
5.00
|
При осуществлении выборки возможны ошибки наблюдения: ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают из-за неточностей, погрешностей при получении сведений о единицах совокупности, когда истинное значение изучаемого признака не совпадает с его зарегистрированным значением. Например, при переписи, когда люди занижают или завышают свой возраст. Ошибки регистрации могут иметь случайный (непреднамеренный) и систематический (тенденциозный) характер. Их можно избежать при правильной организации и проведении наблюдения.
Ошибки репрезентативности возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Ошибки репрезентативности также бывают систематическими и случайными. Систематические ошибки возникают из-за того, что нарушаются условия случайного отбора. Избежать ошибок репрезентативности нельзя, однако, пользуясь методами теории вероятностей, основанными на использовании предельных теорем, эти ошибки можно свести к минимуму. Способы оценки величины случайной ошибки репрезентативности и составляют основу математической теории выборочного метода.
Числовые характеристики генеральной совокупности будем называть генеральными (или теоретическими) параметрами. Однако генеральная совокупность обычно неизвестна и судить о ней приходится по выборке. Но состав выборки случаен, поэтому и выводы о параметрах генеральной совокупности, сделанные на основании выборочных данных, тоже будут иметь случайный характер. Следовательно, ни при каком объеме выборки, вообще говоря, нельзя получить точное значение неизвестного параметра генеральной совокупности, а можно лишь найти его приближенное значение, которое называется оценкой неизвестного параметра по выборке.
Задача статистической оценки параметров заключается в том, чтобы составить такую выборочную характеристику, которая позволила бы получить по возможности наиболее точное и надежное представление о теоретическом параметре. Однако для изучения какого-либо признака генеральной совокупности нужно знать функцию распределения этого признака. Если вид функции распределения известен, то говорят о параметрической задаче, поскольку любое распределение определяется определенным числом параметров. Так, нормальное распределение определяется двумя параметрами:a и s, распределение Пуассона – одним параметром l и т.д. В этих случаях задача статистической оценки сводится к оценке параметров распределения. Если же нет представлений о виде распределения, то говорить о параметрах распределения не имеет смысла, в этом случае говорят о непараметрических задачах.
Одной из основных характеристик выборки является эмпирическая функция распределения 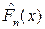 , которая определяется формулой
, которая определяется формулой
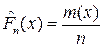 , (3.7)
, (3.7)
где m(x) – число значений среди выборочных значений  , меньших x. Функцию распределения признака F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события X<x, а эмпирическая функция
, меньших x. Функцию распределения признака F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события X<x, а эмпирическая функция 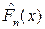 определяет относительную частоту этого события.
определяет относительную частоту этого события.
Пусть F(x;q) – функция распределения величины X, аналитический вид которой известен, но он содержит неизвестный параметр q (для простоты только один). Исследовать все элементы генеральной совокупности для вычисления параметра q не представляется возможным, поэтому об этом параметре приходится судить по выборкам из генеральной совокупности.
Будем предполагать, что мы располагаем выборкой, состоящей из значений  , взятой из генеральной совокупности, с функцией распределения F(x;q). Полученные значения можно рассматривать как частную систему значений независимых случайных величин
, взятой из генеральной совокупности, с функцией распределения F(x;q). Полученные значения можно рассматривать как частную систему значений независимых случайных величин  с одной и той же функцией распределения F(x;q). Величины Xi можно рассматривать как числа (если эксперимент проведен) и как случайные величины (до проведения эксперимента). В дальнейшем мы будем пользовать последней точкой зрения, т.е.
с одной и той же функцией распределения F(x;q). Величины Xi можно рассматривать как числа (если эксперимент проведен) и как случайные величины (до проведения эксперимента). В дальнейшем мы будем пользовать последней точкой зрения, т.е.  – случайные величины, а
– случайные величины, а  – возможные значения выборки, которые меняются от выборки к выборке.
– возможные значения выборки, которые меняются от выборки к выборке.
Пусть
 (3.8)
(3.8)
некоторая функция выборочных значений, которую мы хотим использовать в качестве оценки параметра q. Любая функция выборочных значений, которая не зависит от неизвестных параметров, называется статистикой или статистической оценкой параметра q.
Поскольку любая выборка является случайной, то любая ее статистика также является случайной величиной. Следовательно можно говорить о математическом ожидании, дисперсии и функции распределения случайной величины  . Интерпретация оценки
. Интерпретация оценки  как случайной величины позволяет сформулировать свойства, которыми должна обладать статистическая оценка, чтобы ее можно было считать хорошим приближением к неизвестной генеральной характеристике q.
как случайной величины позволяет сформулировать свойства, которыми должна обладать статистическая оценка, чтобы ее можно было считать хорошим приближением к неизвестной генеральной характеристике q.
Выбор оценки, т.е. функции (3.8), позволяющей получить «хорошее» приближение оцениваемого параметра, – основная задача статистического оценивания. В связи с этим возникает ряд вопросов: какую статистику можно считать наилучшей или по крайней мере «хорошей», т.е. какие требования нужно предъявить к оценкам. Затем следует решить вопрос о способе получения оценок (точечное оценивание); получив ту или иную оценку, необходимо определить точность полученных приближений (интервальное оценивание).
Для того чтобы выбранная оценка была наилучшей, она должна удовлетворять определенным требованиям, или обладать определенными свойствами. Это свойства состоятельности, несмещенности, эффективности.
Оценка  называется состоятельной оценкой параметра q, если
называется состоятельной оценкой параметра q, если  сходится по вероятности к q при n®¥:
сходится по вероятности к q при n®¥:
 .
.
Состоятельность оценки означает, что чем больше объем выборки, тем больше вероятность того, что ошибка оценки не превысит сколь угодно малого положительного числа e. Выполнение условия состоятельности гарантирует от грубых ошибок в оценке неизвестного параметра при достаточно больших объемах выборки.
Оценка  называется несмещённой оценкой параметра q, если математическое ожидание
называется несмещённой оценкой параметра q, если математическое ожидание  равно оцениваемому параметру q , т.е.
равно оцениваемому параметру q , т.е.
 .
.
Если это равенство не выполняется, то оценка может быть либо завышенной, либо заниженной. В обоих случаях это приводит к систематическим ошибкам в оценке параметров. Требование несмещенности гарантирует отсутствие систематических ошибок при оценке параметров. Поэтому, во многих случаях естественно требование несмещенности оценки. Однако, если оценка уже является состоятельной, то при большом объеме выборки требованием несмещенности часто пренебрегают. Требование несмещённости особенно важно при малом объеме выборки.
Оценка  называется эффективной в определенном классе оценок параметра q, если она имеет наименьшую дисперсию среди всех возможных оценок того же самого класса оценок параметра q, вычисленных по выборке одного и того же объема:
называется эффективной в определенном классе оценок параметра q, если она имеет наименьшую дисперсию среди всех возможных оценок того же самого класса оценок параметра q, вычисленных по выборке одного и того же объема:
 .
.
Оценка называется асимптотически эффективной, если с увеличением объема выборки ее дисперсия стремится к нулю, т.е.
 .
.
Справедливо следующее утверждение: если  и
и  при
при 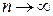 , то
, то  – состоятельная оценка параметра q.
– состоятельная оценка параметра q.
Оценки, являющиеся линейными функциями от выборочных наблюдений, называются линейными. Очень важную роль в эконометрике играют так называемые наилучшие линейные несмещенные оценки, или коротко BLUE-оценки (Best Linear Unbiased Estimators). Такие оценки, являясь линейными и несмещенными, имеют наименьшую дисперсию среди всех возможных оценок данного класса.
На практике при оценке параметров не всегда удается удовлетворить всем выше рассмотренным требованиям. Так, например, может оказаться, что для простоты расчетов целесообразно использовать незначительно смещенную оценку. Наиболее сложным является вопрос о нахождении эффективных оценок. Поэтому на практике часто используются оценки, которые являются не самыми эффективными.
3.3.2. Точечные оценки числовых характеристик
генеральной совокупности
На начальном этапе в качестве оценки той или иной характеристики (математического ожидания, дисперсии, и т.п.) берется выборочная числовая характеристика. Затем, исследуя эту оценку, ее уточняют таким образом, чтобы она удовлетворяла описанным выше требованиям.
Доказано, что выборочная средняя
 (3.10)
(3.10)
является состоятельной и несмещенной оценкой математического ожидания  генеральной совокупности. Эта оценка является эффективной в классе линейных несмещенных оценок. В частности, в случае нормального распределения генеральной совокупности: N(a,s), то оценка (3.10) будет асимптотически эффективной с дисперсией
генеральной совокупности. Эта оценка является эффективной в классе линейных несмещенных оценок. В частности, в случае нормального распределения генеральной совокупности: N(a,s), то оценка (3.10) будет асимптотически эффективной с дисперсией
 (3.11)
(3.11)
Мы уже отмечали, если объем генеральной совокупности больше объема выборки, то между повторной и бесповторной выборками нет существенной разницы. В противном случае эту разность следует учитывать. В случае бесповторной выборки расчеты несколько усложняются. Это связано с тем, что случайные величины  , выражающие значения бесповторной выборки, будут уже зависимыми величинами. Однако здесь также можно показать, что выборочная средняя бесповторной выборки также является состоятельной и несмещенной оценкой генеральной средней (математического ожидания). В случае нормального распределения генеральной совокупности: N(a,s), то оценка также будет асимптотически эффективной с дисперсией
, выражающие значения бесповторной выборки, будут уже зависимыми величинами. Однако здесь также можно показать, что выборочная средняя бесповторной выборки также является состоятельной и несмещенной оценкой генеральной средней (математического ожидания). В случае нормального распределения генеральной совокупности: N(a,s), то оценка также будет асимптотически эффективной с дисперсией
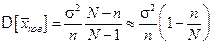 (3.12)
(3.12)
Выборочная дисперсия
 (3.13)
(3.13)
является состоятельной, но смещенной оценкой дисперсии  генеральной совокупности, т.к. доказано, что
генеральной совокупности, т.к. доказано, что
 .
.
Иными словами, выборочная дисперсия оценивает генеральную дисперсию с недостатком. Хотя при n®¥  , и оценка Dвыб является асимптотически несмещенной, в качестве оценки дисперсии s2 лучше брать исправленную дисперсию:
, и оценка Dвыб является асимптотически несмещенной, в качестве оценки дисперсии s2 лучше брать исправленную дисперсию:
 . (3.12)
. (3.12)
Исправленная дисперсия s2 является состоятельной и несмещенной оценкой дисперсии генеральной совокупности.
Из состоятельности оценок s2 и Dвыб следует, что при больших выборках (обычно при n>50) разности между ними практически нет.
Будет ли несмещенная оценка s2 дисперсии эффективной? Оказывается, что нет. Если выборка взята из нормальной генеральной совокупности N(a;s), то эффективная оценка имеет вид
 .
.
Однако в эту формулу входит математическое ожидание, которое, вообще говоря, неизвестно. Следовательно, в таком случае, эффективной оценки вообще не существует, т.е. нижняя граница не достигается ни при какой несмещенной оценки. Однако существует оптимальная оценка и эта оценка совпадает с s2.
В случае бесповторной выборки можно показать, что
 .
.
Поскольку объем генеральной совокупности N, как правило, очень большой (N‡1), то дробь  , причем это равенство является достаточно точным. Поэтому для повторных выборок можно считать, что математическое ожидание выборочной дисперсии равно
, причем это равенство является достаточно точным. Поэтому для повторных выборок можно считать, что математическое ожидание выборочной дисперсии равно  .
.
Выборочная относительная частота (выборочная доля)

где m – число элементов выборки, обладающих заданным признаком, является состоятельной, несмещенной и эффективной оценкой вероятности (генеральной доли)
 ,
,
где M – число элементов генеральной совокупности, обладающих заданным признаком. При этом
 ,
,  .
.
|
из
5.00
|
Обсуждение в статье: Точечные оценки и требования к ним |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

