Метод доверительных интервалов

После получения точечной оценки желательно иметь данные о надежности такой оценки. Понятно, что величина является лишь приближенным значением параметра q. Вычисленная точечная оценка может быть близка к оцениваемому параметру, а может и очень сильно отличаться от него. Точечная оценка не несет информации о точности процедуры оценивания. Особенно важно иметь сведения о надежности оценок для небольших выборок. В таких случаях следует пользоваться интервальными оценками.

Задачу интервального оценивания в самом общем виде можно сформулировать следующим образом: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри этого интервала находится оцениваемый параметр. Здесь существует несколько подходов. Наиболее распространенным методом интервального оценивания является метод доверительных интервалов[1].

Доверительным интервалом для параметра q называется интервал , содержащий неизвестное значение параметра генеральной совокупности с заданной вероятностью g, т.е.

.

Число g называется доверительной вероятностью, а число a=1–g – уровнем надежности. Доверительная вероятность задается априорно и определяется конкретными условиями. Обычно используется g=0,9; 0,95; 0,99 (соответственно, a=0,1; 0,05; 0,01).

Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки n и доверительной вероятности g. При увеличении величины n длина доверительного интервала уменьшается, а с приближением вероятности g к единице – увеличивается.

Часто доверительный интервал строят симметричным относительно точечной оценки, т.е. в виде

, (3.15)

или

.

Здесь число D называется предельной (или стандартной) ошибкой выборки. Однако симметричные интервалы не всегда удается построить, более того, иногда приходится ограничиваться односторонними доверительными интервалами:

или .

Поскольку в эконометрических задачах часто приходится строить доверительные интервалы параметров случайных величин, имеющих нормальное распределение, приведем схемы их нахождения.

3.4.2. Доверительный интервал оценки генеральной
средней при известной генеральной дисперсии

Пусть количественный признак X генеральной совокупности имеет нормальное распределение с заданной дисперсией s² и неизвестным математическим ожиданием a. Для оценки параметра a извлечена выборка X₁, X₂, …, X_n, состоящей из n независимых нормальной распределенных случайных величин с параметрами a и s, причем s известно, а величину a оценивают по выборке:

.

Оценим точность этого приближенного равенства. Для этого зададим вероятность g и попробуем найти такое число D, чтобы выполнялось соотношение

.

Далее воспользуемся свойствами нормального распределения. Известно, что сумма нормально распределенных величин также имеет нормальное распределение. Поэтому средняя величина имеет нормальное распределение, математическое ожидание и дисперсия которой равны

, .

Следовательно,

.

Воспользуемся теперь формулой нахождения вероятностей отклонения нормально распределенной случайной величины от математического ожидания:

,

где F(x) – функция Лапласа. Заменяя X на и s на , получим

,

где . Из последнее равенства находим, что предельная ошибка выборки будет равна

. (3.16)

Тогда

.

Приняв во внимание, что доверительная вероятность задана и равна g, получим окончательный результат.

Интервальная оценка генеральной средней (математического ожидания) имеет вид

, (3.17)

или более кратко

, (3.18)

где число t_g определяется из равенства .

Приведем значения t_g для широко распространенных значений доверительной вероятности:

, , .

Обсудим, как влияет на точность оценивания параметра a объем выборки n, величина среднего квадратичного отклонения s, а также значение доверительной вероятности g.

а) При увеличении n точность оценки увеличивается. К сожалению, увеличение точности (т.е. уменьшение длины доверительного интервала) пропорционально , а не 1/n, т.е. происходит гораздо медленнее, чем рост числа наблюдений. Например, если мы хотим увеличить точность выводов в 10 раз чисто статистическими средствами, то мы должны увеличить объем выборки в 100 раз.

б) Чем больше s, тем ниже точность. Зависимость точности от этого параметра носит линейный характер.

в) Чем выше доверительная вероятность g, тем больше значение параметра t_g, т.е. тем ниже точность. При этом между g и t_g существует нелинейная связь. С увеличением g значение t_g резко увеличивается ( при ). Поэтому с большой уверенностью (с высокой доверительной вероятностью) мы можем гарантировать лишь относительно невысокую точность. (Доверительный интервал окажется широким.) И наоборот: когда мы указываем для неизвестного параметра a относительно узкие пределы, мы рискуем совершить ошибку – с относительно высокой вероятностью.

Отметим, что величина

(3.19)

называется средней ошибкой выборки. Для бесповторной выборки эта формула примет вид

. (3.20)

Тогда предельная ошибка выборки D будет представлять собой t-кратную среднюю ошибку:

.

Пример 3.7. На основе продолжительных наблюдений за весом X пакетов орешков, заполняемых автоматически, установлено, что среднее квадратичное отклонение веса пакетов равно s=10 г. Взвешено 25 пакетов, при этом их средний вес составил . В каком интервале с надежностью 95% лежит истинное значение среднего веса пакетов?

Решение. Логично считать, случайная величина X имеет нормальный закон распределения: . Найдем среднюю ошибку выборки

.

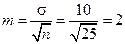Для определения 95%-го доверительного интервала вычислим предельную ошибку выборки

.

Следовательно 95%-й доверительный интервал для истинное значение среднего веса пакетов будет иметь вид

,

или

.

На первый взгляд может показаться, что полученный результат представляет только теоретический результат, поскольку среднее квадратичное отклонение s, как правило, тоже неизвестно и вычисляется по выборочным данным. Однако если выборка достаточно большая, то полученный результат вполне приемлем для практического использования, поскольку функция распределения будет мало отличаться от нормальной, а оценка дисперсии s² будет достаточно близка к истинному значению s². Более того, полученный результат часто используют и в том случае, когда распределение генеральной совокупности отличается нормального. Это обусловлено тем, что сумма независимых случайных величин, в силу центральной предельной теоремы, при больших выборках имеет распределение, близкое к нормальному. â

Пример 3.8. Предположим, что в результате выборочного обследования жилищных условий жителей города на основе собственно-случайной повторной выборки, получен следующий вариационный ряд:

Таблица 3.5

Общая (полезная) площадь жилищ, приходящихся на 1 чел., м2	До 5,0	5,0–10,0	10,0–15,0	15,0–20,0	20,0–25,0	25,0–30,0	30,0 и более
Число жителей

Построить 95%-доверительный интервал для изучаемого признака.

Решение. Рассчитаем выборочную среднюю величину и дисперсию изучаемого признака.

Таблица 3.6

Общая площадь жилищ, приходящаяся на 1 чел., м2	Число жителей, ni	Середина интервала, xi
До 5,0		2,5	20,0	50,0
5,0–10,0		7,5	712,5	5343,8
10,0–15,0		12,5	2550,0	31875,0
15,0–20,0		17,5	4725,0	82687,5
20,0–25,0		22,5	4725,0	106312,5
25,0–30,0		27,5	3575,0	98312,5
30,0 и более		32,5	2697,5	87668,8
Итого		–	19005,0	412250,0

Тогда

; ; .

Средняя ошибка выборки составит

.

Определим предельную ошибку выборки с вероятностью 0,95 ( ):

.

Установим границы генеральной средней

,

или

.

Таким образом, на основании проведенного выборочного обследования с вероятностью 0,95 можно заключить, что средний размер общей площади, приходящейся на 1 чел., в целом по городу лежит в пределах от 18,6 до 19,4 м². â

3.4.3. Доверительный интервал оценки генеральной
средней при неизвестной генеральной дисперсии

Выше была решена задача построения интервальной оценки для математического ожидания нормального распределения, когда его дисперсия известна. Однако на практике дисперсия обычно тоже неизвестна и ее вычисляют по той же самой выборке, что и математическое ожидание. Это приводит к необходимости использования другой формулы при определении доверительного интервала для математического ожидания случайной величины, имеющей нормальное распределение. Такая постановка задачи особенно актуальна при малых объемах выборки.

Пусть количественный признак X генеральной совокупности имеет нормальное распределение N(a,s), причем оба параметра a и s неизвестны. По данным выборки X₁, X₂, …, X_n, вычислим среднее арифметическое и исправленную дисперсию:

, .

Для нахождения доверительного интервала в этом случае строится статистика

, (3.21)

имеющая распределение Стьюдента с числом степеней свободы n=n–1 независимо от значений параметров a и s. Выбрав доверительную вероятность g и зная объем выборки n, можно найти такое число t, что будет выполняться равенство

,

или

.

Отсюда находим

интервальную оценку для генеральной средней (математического ожидания) при неизвестном s:

, (3.22)

или более кратко

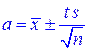. (3.23)

Число t (коэффициент Стьюдента) находится из таблиц для распределения Стьюдента. Отметим, что он является функцией двух аргументов: доверительной вероятности g и числа степеней свободы k=n–1, т.е. t=t(g,n).

Следует быть очень внимательным при использовании таблиц для распределения Стьюдента. Во-первых, обычно в таблицах вместо доверительной вероятности g используют уровень надежности a=1–g. Во-вторых, очень часто в таблицах приводятся значения т.н. одностороннего критерия Стьюдента

, или .

В этом случае в таблицах следует брать значения , если в таблице используется уровень надежности, или , если в таблице используется доверительная вероятность.

Несмотря на кажущееся сходство формул (3.17) и (3.22), между ними имеется существенное различие, заключающееся в том, что коэффициент Стьюдента t зависит не только от доверительной вероятности, но и от объема выборки. Особенно это различие заметно при малых выборках. (Напомним, что при больших выборках различие между распределением Стьюдента и нормальным распределением практически исчезает.) В этом случае использование нормального распределения приводит к неоправданному сужению доверительного интервала, т.е. к неоправданному повышению точности. Например, если n=5 и g=0,99, то, пользуясь распределением Стьюдента, получим t=4,6, а используя нормальное распределение, – t=2,58, т.е. доверительный интервал в последнем случае почти в два раза уже, чем интервал при использовании распределения Стьюдента.

Пример 3.9. Аналитик фондового рынка оценивает среднюю доходность определенных акций. Случайная выборка 15 дней показала, что средняя (годовая) доходность со средним квадратичным отклонением . Предполагая, что доходность акций подчиняется нормальному закону распределения, постройте 95%-доверительный интервал для средней доходности интересующего аналитика вида акций.

Решение. Поскольку объем выборки n=15, то необходимо применить распределение Стьюдента с степенями свободы. По таблицам для распределения Стьюдента находим

.

Используя это значение, строим 95%-доверительный интервал:

,

или

.

Следовательно, аналитик может быть на 95% уверен, что средняя годовая доходность по акциям находится между 8,44% и 12,3%. â