Коэффициент детерминации. Как уж ранее отмечалось, в случае линейной регрессии основными показателями качества

Как уж ранее отмечалось, в случае линейной регрессии основными показателями качества построенного уравнения регрессии служат коэффициент детерминации и критерий Фишера. Использование этих показателей обосновывается в теории дисперсионного анализа. Здесь рассматриваются следующие суммы:

· – общая сумма квадратов отклонений зависимой переменной от средней (TSS);

· – сумма квадратов, обусловленная регрессией (RSS);

· – сумма квадратов, характеризующая влияние неучтенных факторов (ESS).

Напомним, что для моделей, линейных относительно параметров, выполняется следующее равенство

. (6.21)

Исходя из этого равенства, вводился коэффициент детерминации

. (6.22)

В силу определения R² принимает значения между 0 и 1, . Чем ближе R² к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если R²=1, то эмпирические точки (x_i,y_i) лежат на линии регрессии и между переменными Y и X существует функциональная зависимость. Если R²=0, то вариация зависимой переменной полностью обусловлена воздействием неучтённых в модели переменных. Величина R² показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Однако для моделей, нелинейных относительно параметров, равенство (6.21) не выполняется, т.е. . В связи с этим может получиться, что или . Это означает, что коэффициент детерминации, определяемый по формулам (6.22), может быть больше единицы или меньше нуля. Следовательно, R² для нелинейных моделей не является вполне адекватной характеристикой качества построенного уравнения регрессии.

На практике обычно в качестве коэффициента детерминации принимается величина

. (6.23)

Эта величина имеет тот же самый смысл, что и для линейной модели, но при его использовании нужно учитывать все рассмотренные выше оговорки.

Замечание. Величину R² для нелинейных моделей иногда называют индексом детерминации, корень из данной величины R называют индексом корреляции.

Если после преобразования нелинейное уравнение регрессии принимает форму линейного парного уравнения регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции , где z – преобразованная величина независимой переменной, например z=1/x или z=lnx.

Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с результативным признаком. В этом случае линейный коэффициент корреляции по преобразованным значениям даёт лишь приближённую оценку тесноты связи и численно не совпадает с индексом корреляции.

Вследствие близости результатов и простоты расчётов с использованием компьютерных программ для характеристики тесноты связи по нелинейным функциям широко используется линейный коэффициент корреляции ( или 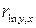). Несмотря на близость значений R_yx и или R_yx и 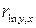, следует помнить, что эти значения не совпадают. Это связано с тем, что для нелинейной регрессии , в отличие от линейной регрессии .

Коэффициент детерминации можно сравнивать с квадратом коэффициента корреляции для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина меньше . Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически, если величина ( – ) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия этих показателей, вычисленных по одним и тем же исходным данным.

Коэффициент детерминации можно использовать при сравнении двух альтернативных уравнений регрессии. Можно выбрать наилучшую из них по максимальному значению коэффициента детерминации. При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной предложенный способ выбора достаточно проста и очевидна. Однако нельзя сравнивать, например, линейную и логарифмические модели. Значения lnY значительно меньше соответствующих значений Y, поэтому неудивительно, что остатки также значительно меньше, но это ничего не решает. Величина R² безразмерна, однако в двух уравнениях она относится к разным понятиям. В одном уравнении она измеряет объясненную регрессией долю дисперсии Y, а в другом – объясненную регрессией долю дисперсии lnY. Если для одной модели коэффициент R² значительно больше, чем для другой, то можно сделать оправданный выбор без особых раздумий, однако, если значения R² для двух моделей приблизительно равны, то проблема выбора существенно усложняется.

Более подробно проблемы спецификации рассматриваются в дополнении 3.

Отметим, что критерий Фишера можно применять только для нормальной линейной классической регрессионной модели. Однако в общем случае, в первую для моделей нелинейных по параметрам, критерий Фишера применять нельзя! Иногда критерий Фишера применяют для линеаризованных моделей, однако здесь следует помнить, что исходное и линеаризованное уравнения не одно и то же, т.е. здесь нужны серьезные оговорки.

Более подробно использования критерия Фишера для линеаризированных моделей смотрите в дополнении 2.

ПРИМЕРЫ

Пример 6.1. Вычислить полулогарифмическую функцию регрессии зависимости доли расходов на товары длительного пользования в общих расходах семьи (Y, %) от среднемесячного дохода семьи (X, тыс. $):

X
Y		13,4	15,4	16,5	18,6	19,3

Решение. Используем стандартные процедуры линейного регрессионного анализа. Для расчетов воспользуемся данными таблицы 6.1:

Табл. 6.1.

№	x	u=lnx	y	uy	u2	y2			A
							9,88	0,12	1,241	0,0154
		0,693	13,4	9,29	0,48	179,56	13,43	-0,03	0,232	0,0010
		1,099	15,4	16,92	1,21	237,16	15,51	-0,11	0,718	0,0122
		1,386	16,5	22,87	1,92	272,25	16,99	-0,49	2,946	0,2363
		1,609	18,6	29,94	2,59	345,96	18,13	0,47	2,524	0,2203
		1,792	19,1	34,22	3,21	364,81	19,07	0,03	0,180	0,0012
Итого		6,579		113,24	9,41	1499,74			7,840	0,4864
Среднее значение	3,5	1,097	15,5	18,87	1,57	249,96			1,307

В соответствии с формулами (6.103) вычисляем

, .

В результате, получим уравнение полулогарифмической регрессии:

. (6.24)

Подставляя в уравнение (6.24) фактические значения x_i, получаем теоретические значения результата . Используя программу Excel, получим следующие данные (на уровне значимости a=0,05):

Табл. 6.3

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,9958
R-квадрат	0,9916
Нормированный R-квадрат	0,9896
Стандартная ошибка	0,3487
Наблюдения
ДИСПЕРСИОННЫЙ АНАЛИЗ
	df	SS	MS	F	Значимость F
Регрессия		57,75	57,75	474,93	0,000026
Остаток		0,49	0,12
Итого		58,24

 

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	9,8759	0,2947	33,51	0,0000047	9,0576	10,6942
Переменная lnX	5,1289	0,2353	21,79	0,0000262	4,4755	5,7823

Из этих данных видно, в частности, что все коэффициенты регрессии статистически значимы. Оценим качество уравнения регрессии. Рассчитаем среднюю ошибку аппроксимации

,

т.е. с точки зрения этого показателя уравнение регрессии подобрано очень хорошо.

Вычислим теперь средний коэффициент эластичности

.

Таким образом, при возрастании среднемесячного дохода семьи на 1% доля расходов на товары длительного пользования в общих расходах семьи возрастет на 0,25% .

Коэффициент детерминации для данной модели совпадает с квадратом коэффициента корреляции . По данным таблицы 6.3 получаем

и .

Коэффициент детерминации показывает, что уравнение регрессии на 99% объясняет вариацию значений признака y, т.е. с точки зрения коэффициента детерминации построенное уравнение регрессии очень хорошо описывает исходные данные.

Для оценки качества данной модели можно использовать критерий Фишера (при предположении, что мы имеем дело с нормальной классической линейной моделью). В этом случае получаем

, .

Поскольку F_набл>F_крит, то гипотеза о случайной природе оцениваемых параметров отклоняется и признается их статистическая значимость и надежность, т.е. построенное уравнение регрессии признается статистически значимым. â

Пример 6.2. Имеются данные о просроченной задолженности по заработной плате за 9 месяцев 2000 г. по Санкт-Петербургу.

Месяцы	Январь	Февраль	Март	Апрель	Май	Июнь	Июль	Август	Сентябрь
Y	387,5	399,9	404,0	383,1	376,9	377,7	358,1	371,9	333,4

а) Оцените МНК коэффициенты линейной модели . Оцените качество построенной регрессии. б) Оцените МНК коэффициенты обратной модели , линеаризуя модель. Оцените качество построенной регрессии. в) Оцените МНК коэффициенты обратной модели , используя численные методы (метод Маркуардта)? г) Проанализируйте полученные результаты.

Решение. а) Используя стандартные процедуры линейного регрессионного анализа (считая, как обычно, t=1 для января 2000 г.), получим:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,846
R-квадрат	0,716
Нормированный R-квадрат	0,675
Стандартная ошибка	12,233
Наблюдения
ДИСПЕРСИОННЫЙ АНАЛИЗ
	df	SS	MS	F	Значимость F
Регрессия		2640,07	2640,07	17,64	0,00403
Остаток		1047,58	149,65
Итого		3687,64
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	410,12	8,89	46,15	5,87E-10	389,11	431,14
Переменная X 1	-6,63	1,58	-4,20	4,03E-03	-10,37	-2,90

Таким образом, линейное уравнение регрессии будет иметь вид

,

причём все коэффициенты регрессии значимы. Коэффициент детерминации равен , т.е. линейная модель удовлетворительно описывает исходные данные. На графике поле корреляции и линейное уравнение регрессии будут выглядеть следующим образом:

В соответствии с построенным уравнением просроченная задолженность по заработной плате за 9 месяцев 2000 г. ежемесячно снижалась на 6,6 млн. руб. Расчётное значение просроченной задолженности за декабрь 1999 г. составило 410,1 млн. руб. Точечный прогноз за октябрь составила: млн. руб.

Оценим точность прогноза. В соответствии с линейным регрессионным анализом, находим предельную ошибку индивидуального прогноза (на уровне значимости a=0,05):

В результате, доверительный интервал для прогнозного значения будет иметь вид

.

Точность прогноза составила .

б) Линеаризуем модель, полагая v=1/y. Составляем расчётную таблицу.

Месяцы	t	y	v=1/y	tv	t2	v2
Январь		387,6	0,00258	0,0026		0,0000067	0,00247	0,0001134	0,00000001286
Февраль		399,9	0,00250	0,0050		0,0000063	0,00252	-0,0000145	0,00000000021
Март		404,0	0,00248	0,0074		0,0000061	0,00256	-0,0000885	0,00000000783
Апрель		383,1	0,00261	0,0104		0,0000068	0,00261	-0,0000020	0,00000000000
Май		376,9	0,00265	0,0133		0,0000070	0,00266	-0,0000076	0,00000000006
Июнь		377,7	0,00265	0,0159		0,0000070	0,00271	-0,0000618	0,00000000382
Июль		358,1	0,00279	0,0195		0,0000078	0,00276	0,0000345	0,00000000119
Август		371,9	0,00269	0,0215		0,0000072	0,00281	-0,0001177	0,00000001385
Сентябрь		333,4	0,00300	0,0270		0,0000090	0,00286	0,0001442	0,00000002081
Итого:		3392,6	0,02395	0,1227		0,0000639	0,02395		0,00000006063
Среднее		376,96	0,002661	0,0136	31,67	0,0000071

Вычисляем

,

.

В результате, получим уравнение обратной регрессии:

.

Используя программу Excel получим следующие данные (на уровне значимости a=0,05):

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,837
R-квадрат	0,700
Нормированный R-квадрат	0,657
Стандартная ошибка	9,30686E-05
Наблюдения

 

ДИСПЕРСИОННЫЙ АНАЛИЗ
	df	SS	MS	F	Значимость F
Регрессия		1,41557E-07	1,41557E-07	16,34	0,00492
Остаток		6,06323E-08	8,66176E-09
Итого		2,02189E-07
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	0,002418	6,76E-05	35,76	3,47E-09	0,00226	0,00258
Переменная lnX	0,0000486	1,20E-05	4,04	0,00492	2,02E-05	7,70E-05

Качество линеаризованного уравнения довольно высокое (R²=0,7). Этот вывод подтверждается и с точки зрения критерия Фишера (отметим, что для линеаризованных моделей, при определённых оговорках, можно применить критерий Фишера). Однако в рассматриваемом случае МНК применялся не к y, а к обратным значениям 1/y, а это существенная разница. Проанализируем исходную, нелинеаризированную, модель.

t	y						A
	387,6	405,42	-17,821	317,58	113,30	810,26	4,60
	399,9	397,59	2,309	5,33	526,45	425,83	0,58
	404,0	390,06	13,942	194,37	731,40	171,68	3,45
	383,1	382,81	0,294	0,09	37,75	34,22	0,08
	376,9	375,82	1,082	1,17	0,00	1,29	0,29
	377,7	369,08	8,620	74,30	0,55	62,02	2,28
	358,1	362,58	-4,480	20,07	355,53	206,64	1,25
	371,9	356,31	15,595	243,19	25,56	426,43	4,19
	333,4	350,24	-16,844	283,71	1897,09	713,52	5,05
	3392,6		2,696	1139,81	3687,64	2851,90	21,77
	376,96						2,42

Из таблицы видно, что для данной модели

.

Отметим, что для нелинейных моделей, оцененных МНК, эта сумма всегда равна нулю. Следовательно, оценки исходной нелинейной модели будут смещёнными.

Отсюда, в частности, следует, что равенство не выполняется. Действительно,

.

В связи с этим, для коэффициента детерминации можно получить два разных значения:

, или .

Это означает, что коэффициент детерминации для нелинейных моделей не всегда является адекватной характеристикой. Отметим, что в компьютерных программах для вычисления коэффициента детерминации в основном используют второе равенство.

Сделаем прогноз по полученному уравнению обратной модели и оценим его точность. Точечный прогноз за октябрь составит:

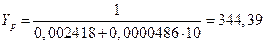млн. руб.

Оценим точность прогноза. В соответствии с линейным регрессионным анализом, находим предельную ошибку индивидуального прогноза по линеаризированному уравнению (на уровне значимости a=0,05):

В результате, доверительный интервал для прогнозного значения будет иметь вид

.

Точность прогноза для преобразованной переменной v составляет 9,4%. Однако мы имеем дело нес обратными величинами v=1/y, а с y. Переходя к исходной переменной, получим следующий доверительный интервал

.

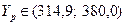Точность прогноза для непреобразованной переменной y составляет уже 18,9%. Этот результат показывает, что исходное и преобразованное уравнения дают, вообще говоря, разный результат.

в) Оценим МНК коэффициенты обратной модели

,

используя численные методы (метод Левенберга-Маркуардта). Для этого воспользуемся программой STATISTIKA. Программа выдаёт следующие результаты.

Уравнение регрессии имеет вид

с коэффициентом детерминации R²=0,6947. Для сравнений приведем результаты вычислений.

Видно, что численные методы дают вполне удовлетворительный результат. Более того, они позволяют провести также и некоторый статистический анализ полученной модели (хотя и не такой полный по-сравнению с линейными моделями). Таким образом, как показывает данный пример, линеаризация не всегда даёт более лучший результат по-сравнению с численными методами.

г) Сделаем некоторые выводы. Отметим, что коэффициенты детерминации для обеих моделей (линейной и обратной) практически не отличаются друг от друга: R²=0,716 для линейной модели и R²=0,691 для обратной модели. Поэтому обе модели с точки зрения коэффициента детерминации равноценны. Однако при оценке точности прогноза лучше использовать, как мы видели, линейную модель. Таким образом, использование обратной модели для интерпретации имеющихся результатов не совсем оправдано. С точки зрения статистических свойств в данном случае лучше использовать линейную модель. â

Пример 6.3. Имеются данные о зависимости расхода топлива (Y, г/на т·км) от мощности двигателя грузовых автомобилей общего назначения (X, л.с.):

X
Y

а) Оцените МНК коэффициенты линейной модели . Оцените качество построенной регрессии. б) Оцените МНК коэффициенты степенной модели , линеаризуя модель. Оцените качество построенной регрессии.

Решение. а) Используя стандартные процедуры линейного регрессионного анализа, получим:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,8378
R-квадрат	0,7019
Нормированный R-квадрат	0,6688
Стандартная ошибка	12,8383
Наблюдения
ДИСПЕРСИОННЫЙ АНАЛИЗ
	df	SS	MS	F	Значимость F
Регрессия		3493,3	3493,3	21,19	0,001284
Остаток		1483,4	164,8
Итого		4976,7
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	103,866	9,993	10,39	0,0000	81,261	126,471
Переменная X	-0,3388	0,0736	-4,60	0,0013	-0,5053	-0,1723

Таким образом, линейное уравнение регрессии будет иметь вид

,

причём все коэффициенты регрессии значимы. Коэффициент детерминации равен , т.е. линейная модель удовлетворительно описывает исходные данные.

На графике поле корреляции и линейное уравнение регрессии будут выглядеть следующим образом:

б) Линеаризуем модель . В данном случае линеаризация производится путем логарифмирования обеих частей уравнения:

.

В результате получаем линейное уравнение регрессии:

,

где . Таким образом, степенная модель свелась к линейной модели с ее методами оценивания параметров и проверки гипотез. Составляем расчетную таблицу.

№	x	y	u=lnx	v=lny	uv	u2	v 2
			4,248	4,477	19,022	18,050	20,047	4,4714	0,0059	0,00003
			4,248	4,431	18,824	18,050	19,632	4,4714	-0,0406	0,00165
			4,317	4,477	19,331	18,641	20,047	4,4119	0,0655	0,00429
			4,443	4,331	19,240	19,737	18,755	4,3038	0,0270	0,00073
			4,575	4,263	19,501	20,928	18,170	4,1897	0,0730	0,00533
			4,745	3,951	18,748	22,514	15,612	4,0427	-0,0914	0,00836
			4,787	3,951	18,917	22,920	15,612	4,0059	-0,0547	0,00299
			5,011	3,829	19,184	25,106	14,658	3,8132	0,0154	0,00024
			5,165	4,143	21,398	26,675	17,166	3,6801	0,4631	0,21444
			5,193	3,045	15,810	26,967	9,269	3,6557	-0,6112	0,37357
			5,481	3,555	19,486	30,037	12,640	3,4073	0,1481	0,02193
Итого:			52,213	44,453	209,460	249,625	181,609			0,6336
Среднее	125,18	61,45	4,747	4,041	19,042	22,693	16,510

Рассчитываем коэффициенты линеаризованного уравнения регрессии:

,

, .

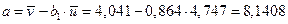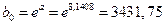В результате, получим уравнение степенной регрессии:

.

Коэффициент эластичности в данном случае равен . Это означает, что с увеличением мощности двигателя грузового автомобиля на 1% расход топлива в расчёте на 1 т-км снижается примерно на 0,86%.

Используя программу Excel получим следующие данные (на уровне значимости a=0,05):

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,8233
R-квадрат	0,6778
Нормированный R-квадрат	0,6420
Стандартная ошибка	0,2653
Наблюдения
ДИСПЕРСИОННЫЙ АНАЛИЗ
	df	SS	MS	F	Значимость F
Регрессия		1,3327	1,3327	18,93	0,001847
Остаток		0,6336	0,0704
Итого		1,9663
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	8,141	0,946	8,609	0,0000123	6,002	10,280
Переменная lnX	-0,864	0,198	-4,351	0,0018473	-1,313	-0,415

Качество линеаризованного уравнения довольно высокое (R²=0,678). Этот вывод подтверждается и с точки зрения критерия Фишера (напомним, что для линеаризованных моделей, при определённых оговорках, можно применить критерий Фишера). Однако в рассматриваемом случае МНК применялся не к y, а к их логарифмам lny, а это существенная разница. Проанализируем исходную, нелинеаризированную, модель.

x	y						A
		87,483	-0,517	0,27	704,66	677,49	0,59
		87,483	3,483	12,13	508,30	677,49	3,98
		82,422	-5,578	31,11	704,66	439,65	6,77
		73,977	-2,023	4,09	211,57	156,82	2,73
		66,003	-4,997	24,97	91,12	20,69	7,57
		56,979	4,979	24,79	211,57	20,03	8,74
		54,922	2,922	8,54	91,12	42,67	5,32
		45,295	-0,705	0,50	89,39	261,13	1,56
		39,649	-23,351	545,29	89,39	475,50	58,90
		38,696	17,696	313,13	1636,57	517,97	45,73
		30,182	-4,818	23,21	699,84	977,95	15,96
			-12,909	988,03	5038,18	4267,39	157,85
125,18	61,45						14,35

Из таблицы видно, что для данной модели

.

Следовательно, оценки исходной нелинейной модели будут смещёнными.

Для коэффициента детерминации можно получить два разных значения:

, или .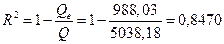

Это означает, что полученное уравнение достаточно хорошо описывает исходные данные и этот коэффициент выше, чем для коэффициента детерминации линейной регрессии. Хотя средний коэффициент аппроксимации не очень низкий .

Сделаем прогноз по полученному уравнению степенной модели и оценим его точность. При мощности двигателя x=70 л.с. расход топлива на 1 т-км составит