Статистический анализ коэффициентов регрессии

Перейдём теперь к оценке значимости коэффициентов регрессии 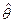и построению доверительного интервала для параметров регрессионной модели q. В п.1.3 мы получили

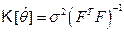. (6.42)

В силу этого оценка 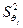дисперсии 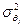коэффициента регрессии q_j определится по формуле:

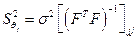, (6.43)

где B_jj – диагональный элемент матрицы B. Величина 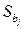называется стандартной ошибкой коэффициента регрессии .

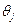В предыдущих пунктах мы показали, что вектор оценок 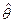имеет нормальное распределение со средним q и ковариационной матрицей (6.46). Тогда

.

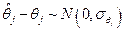Случайная величина (6.45) имеет распределение c²-распределение и оценки 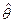и S² независимы. Отсюда получаем, что величина

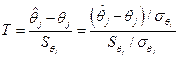(6.44)

имеет распределение Стьюдента с n–m степенями свободы. Поэтому q_j значимо отличается от нуля на уровне значимости a, если

.

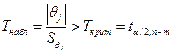Из (6.42) также следует, что доверительный интервал для параметра q_j имеет вид

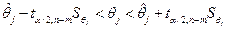. (6.45)

Наряду с интервальным оцениванием коэффициентов регрессии весьма важным для оценки точности определения зависимой переменной (прогноза) является построение доверительного интервала для функции регрессии или для условного математического ожидания зависимой переменной M[Y|X=x]. Ранее такой интервал был получен для парной линейной регрессии. Обобщая полученные результаты, можно получить доверительный интервал для условного математического ожидания M[Y|X=x]:

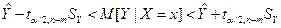, (6.46)

где

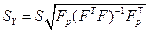(6.47)

– стандартная ошибка прогноза среднего значения. Здесь

.

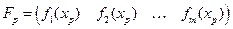Аналогично строится доверительный интервал для индивидуальных значений зависимой переменной :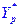

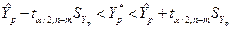, (6.48)

где

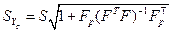. (6.49)

Более подробное обсуждение этого вопроса см. лекцию 7.

Дополнение 2.
КРИТЕРИЙ ФИШЕРА

Как уже говорилось, в рамках линейной классической регрессионной модели общее качество уравнения регрессии оценивается при помощи методов дисперсионного анализа. Схема дисперсионного анализа, имеет следующий вид:

Компоненты дисперсии	Сумма квадратов	Число степеней свободы, df	Средние квадраты
Регрессия		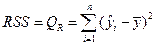m–1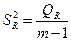
Остаточная		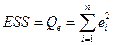n–m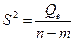
Общая		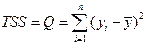n–1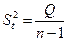

Определение дисперсии на одну степень свободы приводит дисперсии к сравниваемому виду. Средние квадраты представляют собой несмещённые оценки соответствующих дисперсий.

Проверка гипотезы о значимости уравнения регрессии осуществляется на основе дисперсионного анализа сравнения объяснённой и остаточной дисперсий:

H₀: (объяснённая дисперсия) = (остаточная дисперсия);

H₁: (объяснённая дисперсия) > (остаточная дисперсия).

Строится F-статистика

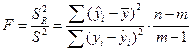. (6.50)

В рамках нормальной линейной регрессионной модели, случайные величины 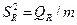и 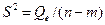будут иметь c²-распределение соответственно с m и n–m степенями свободы. Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим случайную величину, описывающуюся распределением Фишера с теми же степенями свободы:

Полученную F-статистику можно использовать для проверки нулевой гипотезы 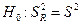. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга, т.е. 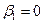. Эмпирическое уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики

,

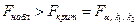где 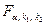– табличное значение F-критерия Фишера, определённое на уровне значимости a при k₁=1 и k₂=n–2 степенях свободы.

Величина F-критерия связана с коэффициентом детерминации R²:

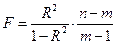. (6.51)

Таким образом, малым значениям F соответствуют малые значения R².

Отметим, что критерий Фишера можно применять только обобщенной нормальной линейной классической регрессионной модели. Однако в общем случае, особенно для моделей нелинейных по параметрам, критерий Фишера применять нельзя! Иногда критерий Фишера применяют для линеаризованных моделей, однако здесь следует помнить, что исходное и линеаризованное уравнения не одно и то же, т.е. здесь нужны серьезные оговорки.

F-критерий Фишера можно использовать для сравнения двух альтернативных уравнений регрессии в рамках классической нормальной линейной модели. В данном случае его величина рассчитывается по формуле

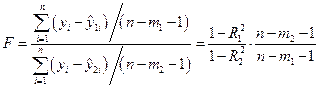. (6.52)

где 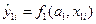, 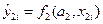– расчётные значения переменной y, полученные на основе первого и второго вариантов моделей соответственно, различающиеся, быть может, формой зависимости f и количества факторов; n₁ и n₂ – количества факторов в первом и втором вариантов соответственно.

Критерий (6.98) является двухсторонним. Особенности его применения состоят в следующем. Если выполняется соотношение

,

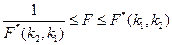то рассматриваемые альтернативные варианты модели признаются равнозначимыми с точки зрения точности описания процесса y_i.

Если

,

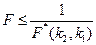то выбор следует сделать в пользу первого варианта модели, а если

,

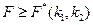то – в пользу второго.

Здесь 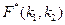– табличное значение критерия Фишера, выбранное для заданного уровня надёжности a и числе степеней свободы 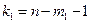и .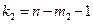

Если сравнение производится с простой линейной регрессией, то 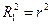и m₁=2. В результате критерий (6.94) примет вид

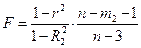. (6.53)

Тогда если

,

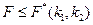то различия между 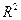и 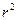не существенны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата. Если

,

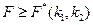То различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции неправильна.

Дополнение 3.
СПЕЦИФИКАЦИЯ МОДЕЛИ