Классическая модель основания Винклера

Понятие модели:модели эвристические, натурные, математические.

Модель - это система, исследование которой служит средством для получения информации о другой системе, это упрощённое представление реального устройства и/или протекающих в нём процессов, явлений.

Основные виды моделей. По способу отображения действительности различают три основных вида моделей -- эвристические, натурные и математические.

Эвристические модели. Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальнаяинформационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.

Натурные модели. Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие: Физические модели. Ими являются реальные изделия, образцы, экспериментальные и натурные модели, когда между параметрами системы и модели одинаковой физической природы существует однозначное соответствие; Технические модели; Социальные модели;Экономические модели, например, Бизнес-модель;

Математические модели. Математические модели -- формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:

аналитические модели. Их решения ищутся в замкнутом виде, в виде функциональных зависимостей; численные модели. Их решения -- дискретный ряд чисел (таблицы); формально-логические информационные модели -- это модели, созданные на формальном языке; эталонная модель.

Построение математических моделей возможно следующими способами: аналитическим путём, то есть выводом из физических законов, математических аксиом или теорем; экспериментальным путём, то есть посредством обработки результатов эксперимента и подбора аппроксимирующих (приближённо совпадающих) зависимостей.

Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования -- с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула -- это разновидность модели и, следовательно, не является абсолютной истиной, а всего лишь этап на пути её познания.

Модули упругости

Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела (материала, вещества) упруго деформироваться (то есть не постоянно) при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона диаграммы напряжений-деформаций: где: E — модуль упругости; — напряжение, вызываемое в образце действующей силой (равно силе, делённой на площадь приложения силы); — упругая деформация образца, вызванная напряжением (равна отношению изменения размера образца после деформации к его первоначальному размеру).

В наиболее распространенном случае зависимость напряжения и деформации линейная (закон Гука): .

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:

· Модуль Юнга (E) характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия(удлинения). Часто модуль Юнга называют просто модулем упругости.

· Модуль сдвига или модуль жесткости (G или ) характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения). Модуль сдвига является одной из составляющих явления вязкости.

· Модуль объёмной упругости или Модуль объёмного сжатия (K) характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения (объёмного напряжения), одинакового по всем направлениям (возникающего, например, при гидростатическом давлении). Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля (для несжимаемой жидкости — бесконечен).

Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе. Гомогенные и изотропные материалы (твердые), обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.

Модель Винклера

Классическая модель основания Винклера

Классической расчетной механической моделью основания Винклера является ряд не связанных между собой упругих пружин, закрепленных на абсолютно жестком основании. Штамп, приложенный к поверхности такой модели, при нагружении вдавливается на глубину S, пропорциональную среднему давлению P, и при снятии нагрузки возвращается в исходное положение. Поверхность этой модели за пределами штампа не деформируется, т.е. не учитывается работа грунта за пределами фундамента.

Механические свойства модели Винклера характеризуются коэффициентом жесткости (постели) K₁ (C₁). По физическому смыслу коэффициент жесткости означает величину усилия в тонна-силах, которое необходимо приложить к 1 м² поверхности основания, чтобы последнее осело на 1 м. Размерность K₁ (C₁) – тс/м³. Согласно гипотезе Винклера [7] коэффициент жесткости в i-й точке грунта равен отношению давления 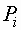на грунт в этой точке к ее осадке :

, Приведённое уравнение справедливо при условии, когда среднее давление под подошвой фундамента P не превышает R – расчетного сопротивления грунта для данного вида грунта и фундамента. В противном случае (согласно [6; 7]) необходимо использовать модели нелинейно-деформируемого основания или снижать величину среднего давления P, увеличивая размеры площади фундаментов.

В классической постановке коэффициент постели модели Винклера зависит только от вида грунта и принимается постоянным по контактной площади основания и фундамента. Определить EF можно по формуле

EF(Z) = K₁F – по направлению оси Z (при вертикальной нагрузке);

где F – контактная площадь основания и фундамента.

Кроме того, эти значения могут быть использованы как исходные данные для КЭ-10, если коэффициент постели постоянен по длине элемента.

Модифицированная модель основания Винклера

Модифицированная модель основания Винклера является универсальной, снимает все вышеприведённые ограничения классических моделей основания и в общем случае характеризуется двумя параметрами [9]:

K₁ – коэффициент жесткости линейно деформируемого основания при сжатии при действии вертикальной нагрузки, тс/м³; K₂ – коэффициент жесткости линейно деформируемого основания при сдвиге при действии горизонтальной нагрузки, тс/м³.

Здесь в понятие коэффициента жесткости K₁ вкладывается другой смысл по сравнению с аналогичным параметром C₁ классической модели Винклера. В данном случае K₁ учитывает не только вид грунта (единственный фактор, который как отмечалось выше, характеризует классическую модель Винклера), но и такие важнейшие факторы, как форму и размеры фундаментов, переменные свойства грунтов по глубине основания и в плане сооружения, работу грунта за пределами фундамента.

Кроме того, модифицированная модель Винклера позволяет с помощью параметра K₂ учитывать совместные горизонтальные деформации оснований и фундаментов при действии горизонтальных нагрузок. Учитывая приближенность исходных данных по определению деформаций основания при действии горизонтальной нагрузки, рекомендуется принимать К₂ = 0,7 К₁.

Коэффициент жесткости K₁ вычисляется по формуле (6.1), исходя из ожидаемых (предварительно вычисленных) осадок поверхности основания S.

Нормы [6] рекомендуют для расчёта осадки S метод послойного суммирования с применением расчётной схемы основания в виде линейно деформируемого полупространства или слоя конечной толщины с учетом формы и размеров фундаментов, свойств грунта на глубине.

Полученные значения коэффициентов жесткости (постели) K₁, K₂ могут использоваться в качестве исходных данных для КЭ-51, 55 при определении жесткостных характеристик EF по формулам:

EF(Z) = K₁ F – по направлению оси Z (при вертикальной нагрузке);

EF(X) = K₂ F – по направлению оси X (при горизонтальной нагрузке);

EF(Y) = K₂ F – по направлению оси Y (при горизонтальной нагрузке),

где F – контактная площадь основания и фундамента.