 |
Главная |
Точки самопересечения
|
из
5.00
|
Исследование и изображение кривой,
Заданной параметрически
Курсовая работа
| Курсовая работа защищена на оценку «_________ » «__»_________2014 г. | Исполнитель:Бажина Т.О., студентка Б-21 группы математического факультета очной формы обучения Руководитель:доктор физико-математических наук, профессор Мухин Ю.Н. |
Екатеринбург 2014.
Содержание
ВВЕДЕНИЕ……………………………………………………………………3
Исследование кривой…………………………………………………………5
1.Область определения………………………………………………………......5
2.Симметрия относительно осей координат, начала координат и прямой x=y
……………………………………………………………………………………6
3.Точки самопересечения………………………………………………………..8
4.Точки пересечения с осями координат……………………………………….9
5. Поведение на концах области определения………………………………....9
6. Уходы в бесконечность………………………………………………………10
7.Асимптоты……………………………………………………………………..11
8.Проверка на гладкость………………………………………………………...13
9.Вертикальные и горизонтальные касательные………………………………14
10.Обыкновенные точки, подозреваемые на перегиб…………………………16
11.Таблица поведения кривой…………………………………………………..18
12.Изображение кривой ………………………………………………………...19
Заключение……………………………………………………………………...20
Библиографический список источников…………………………………....21
ВВЕДЕНИЕ
В доисторические времена человек наблюдал за природными явлениями, формой каких-либо предметов или физических тел. Лучи света, очертания стволов деревьев, листьев растений, линия горизонта, дуга радуги – все это непосредственно привлекало первобытных людей. Эти явления, наблюдаемые многократно, послужили основой для постепенного установления линии.
История развития изучения кривых обширна. Она захватывает почти 40 столетий и связана с именами таких великих математиков как Менехм, Архимед, Декарт, Брианшон, Паскаль, Штейнер, Шаль, Понселе и другие.
В настоящее время в курсах высшей математики широко освещаются методы построение графика функции. Вместе с тем построение кривых, задаваемых параметрически, уделяется мало внимания, и многие стороны этого более сложного исследования почти не затрагиваются. Как следствие, практическая работа, связанная с параметрически заданными кривыми и их построения, представляют собой определенные трудности. В связи с этим тема работы является актуальной.
Для нас, как для будущих учителей математики, исследование и изображение кривых является также немаловажным и выполняет первостепенные функции. Исследование кривой развивает аналитическое и логическое мышление, позволяет правильно конкретизировать мысли, излагая какой-либо научный материал. Навыки изображения кривой помогают решать задачи на построение. С помощью исследования методом дифференцирования развивается чувство абстрактности. А после построения кривой можно наглядно убедиться в правильности и точности всего исследования.
Таким образом, данная тема является особо актуальной для студентов педагогических ВУЗов математической направленности.
Цель исследования: освоить методы исследования и построения плоских кривых, заданных параметрическим способом в прямоугольной системе координат.
Задачи исследования:
1.Изучить литературу по теме курсовой работы.
2. Провести исследование по данному плану.
3. Построить кривую.
Исследование кривой
Исследовать плоские кривые, заданные векторно. Изучить форму кривой:
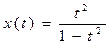
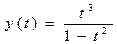
Область определения.
Областью определения называется множество, на котором задается функция.
Если задана функция, которая действует из одного множества в другое, то множество, из которого действует функция, называется областью определения.
Пусть задано отображение
f: X→Y.
Множество X называется областью определения функции f и обозначается D(f).
Если функция задана параметрически, то

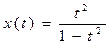
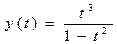
Найдем область определения для нашей кривой:
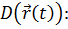
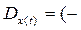

 ;-1)
;-1)  (-1;1)
(-1;1)  (1;+
(1;+ 
 )
)
 (-
(-  ;-1)
;-1) 
 (-1;1)
(-1;1)  (1;+
(1;+ 
 )
)
Таким образом, 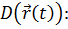
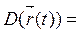 (-
(-  ;-1)
;-1) 
 (-1;1)
(-1;1)  (1;+
(1;+ 
 ).
).
"Концы": -  , -1-0, -1+0, 1-0, 1+0, +
, -1-0, -1+0, 1-0, 1+0, + 
Область определения R, кроме t= 
Получили, что кривая состоит из трёх ветвей
2.Симметрия относительно осей координат, начала координат и прямой y=x.
1) Симметрия относительно осей Ох и Oy.
Две точки А иА1 называются симметричными друг другу относительно прямойm, если прямаяm перпендикулярна отрезку АА1 и проходит через его середину. Прямую m называют осью симметрии.
При сгибании плоскости чертежа по прямойm – оси симметрии симметричные фигуры совместятся.
Симметрия относительно оси Ox:
 x(t) = x(-t)
x(t) = x(-t)
y(t) =- y(-t)
Если x(t) 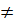 x(-t) или y(t)
x(-t) или y(t) 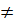 -y(-t), то кривая не симметрична относительно оси Ox
-y(-t), то кривая не симметрична относительно оси Ox
Симметрия относительно оси Oy:
 x(t) = -x(-t)
x(t) = -x(-t)
y(t) =y(-t)
Если x(t)  x(-t) или y(t)
x(-t) или y(t) 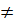 y(-t), то кривая не симметрична относительно оси Oy.
y(-t), то кривая не симметрична относительно оси Oy.
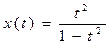
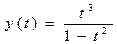
a) Относительно оси Ох. Достаточное условие симметрии:
x(-t)=x(t)
y(-t)=-y(t)

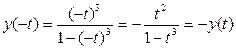
Следовательно, кривая симметрична относительно оси Ох.
b) Относительно оси Оу. Достаточное условие симметрии:
x(-t)=-x(t)
y(-t)=y(t)
 т.е. х(t) не является нечетной.
т.е. х(t) не является нечетной.
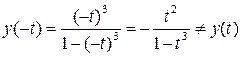 , т.е. у(t) не является четной.
, т.е. у(t) не является четной.
Таким образом, симметрия относительно Оy не установлена.
2) Симметрия относительно начала системы координат.
Достаточное условие симметрии: 
 x(t) = -x(-t)
x(t) = -x(-t)
y(t) = -y(-t)
Если x(t) 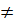 -x(-t) или y(t)
-x(-t) или y(t) 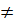 -y(-t), то кривая не симметрична относительно начала системы координат.
-y(-t), то кривая не симметрична относительно начала системы координат.
По доказанному ранее уже известно, что x(t) является четной функцией, т.е.
x(-t)= x(t).
В связи с этим, симметрия относительно начала координат не установлена.
3) Симметрия относительно прямой у=х
Пусть М(х(t), y(t)) 
M´ симметрична М относительно прямой y=x
Тогда M  (y(t), x(t))
(y(t), x(t)) 
Это означает, что существует t1:M  (x(t1), y(t1))
(x(t1), y(t1)) 
t1 – функция от t должна быть биекцией D на себя, тогда
 x(t) = y(t1)
x(t) = y(t1)
y(t) = x(t1)
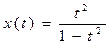
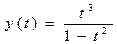
Чтобы определить симметрию относительно прямой y=x, нужно решить следующую систему:
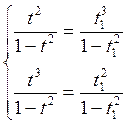

 →
→ 
Если подставить в данную систему t =  , то система не имеет решение. Симметрия относительно прямой у=х не установлена.
, то система не имеет решение. Симметрия относительно прямой у=х не установлена.
Точки самопересечения.
M (x(t), y(t)) называется точкой самопересечения, если существует такое значение параметра t, что


Чтобы найти точки самопересечения, решим следующую систему уравнений:

 (1)
(1)
 (2)
(2)
Разделим уравнение (1) на уравнение (2) почленно:
 ;
; 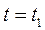
 нет точек самопересечения.
нет точек самопересечения.
4. Точки пересечения с осями координат. 
А) Найдем точки пересечения γ с осью Оy:
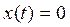 ;
; 
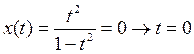 ;
; 
Итак, точка О (0;0) – точка пересечения γ с Оy.
Б) Найдем точки пересечения γ с осью ox:
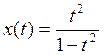 ;
; 
 ;
; 
Итак, точка О (0;0) – точка пересечения γ с Ох.
Таким образом, имеем точку пересечения с осями координат:
О (0;0)- точка пересечения γ с Ох и Оу.
|
из
5.00
|
Обсуждение в статье: Точки самопересечения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

