Принцип возрастания энтропии

 

Наиболее вероятным развитием системы является такое, при котором полная производная энтропии больше нуля:

(*)

Этот принцип сформулировал Клаузиус.

Имея этот принцип, можем получить соответствующее распределение.

Условие (*) означает, что если система выведена из состояния равновесия, то она движется к равновесию по этому закону.

Тогда в состоянии равновесия энтропия системы экстремальна (max)

Так как условие имеется условие нормировки, то имеем условный экстремум, а если бы не было условия нормировки, то был бы абсолютный экстремум.

 

§18*. Статистическая сумма и её свойства

 

Мы определили каноническое распределение:

,

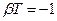
и - это сумма по состояниям, а не по энергетическим уровням.

Энтропия:

Тогда, учитывая язык термодинамики , получаем:

Введём свободную энергию Гельмгольца:

Тогда

(10)

Получаем, что определяется через :

Тогда можем записать:

Из (10) получаем:

Мы будем часто использовать это равенство (здесь в энергетических единицах).

Используем определение для нахождения . Запишем определение среднего:

Эту сумму можно найти, используя дифференцирование по параметру :

Но ведь , тогда:

Используем равенство (10):

Тогда:

А в духе термодинамики , тогда:

Мы получили связь между энергией и свободной энергией Гельмгольца .

Мы получили связь 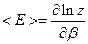между энергией и статистической суммой, где

, а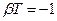

Запишем определение :

Найдём . По определению:

Подставим сюда выражение для 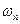и получим:

, здесь сумма – это сумма по состояниям.

Используем дифференцирование по параметру :

Тогда наше выражение примет вид:

По определению , тогда:

Раньше мы получили соотношение

Тогда:

(11)

Покажем, что равенство верно:

Выражение (11) можно связать с :

Ранее мы получили, что:

Тогда:

Теперь, если пишем это равенство для термодинамики, то и

Величина - это теплоёмкость при постоянном объёме (в термодинамике). Это теплоёмкость всей системы.

Тогда:

- линейная аппроксимация

здесь - безразмерная, а - температура в энергетических единицах.

Удельная теплоёмкость – это теплоёмкость в расчёте на единицу массы.

-теплоёмкость в расчёте на одну частицу

Тогда:

Отсюда следует не отрицательность теплоёмкости .

 

§19*. Функция распределения вероятностей по энергии и распределение Гаусса

 

Поскольку величина относительного среднеквадратичного отклонения для энергии значительно меньше 1:

то функция распределения этой величины(энергии) описывается узкой функцией с максимумом:

Ширина максимума очень мала, т.к. .

Так как максимум резкий, то часто эту функцию распределения аппроксимируют Гауссовым распределением:

Константы и легко находятся.

- из условия нормировки:

Тогда:

Интеграл является табличным.

Окончательно для получаем:

Найдём константу через :

Используем дифференцирование по параметру, где мы обозначим :

Но , тогда:

Очевидно, что , т.к.:

-чётная

-как нечётная функция в симметричных пределах

Имеем тогда для :

(12)

Т.к. , то удобно записывать выражение (12) так:

(13)

где .

Зависимости (12) и (13) разные, это надо помнить.

Тогда можно написать:

Окончательно получаем:

Когда мы писали - то получали центрированную случайную величину.

Перейдём к нормированным функциям, т.е. перейдём от . Обозначим , тогда от функции переходят к :

(14)

здесь для случайной величины :

и

Выражение (14) – это функция Гаусса, в ней всё удобно считать.