ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ИНДИВИДУАЛЬНЫХ

ЗАДАНИЙ

1. Перед решением задач необходимо познакомиться с теорией по указанной литературе и конспектами лекций, посмотреть примеры реше­ния задач в методических указаниях и «Сборнике задач по общему курсу физики» под редакцией B.C. Волькенштейн.

2. Работа выполняется в отдельной тетради с указанием группы, ва­рианта, фамилии и инициалов.

3. При решении задач необходимо указать её номер, искомые дан­ные, проанализировать содержание задачи и указать в ней основные зако­ны и формулы, отражающие физический процесс, дать решение и ответ.

4. Задачи следует решать в общем виде, не производя вычислений промежуточных величин.

5. Получив окончательную формулу, выражающую искомую ве­личину, после вычисления проверить по правилам размерности, дает ли эта формула размерность искомой величины в системе СИ.

6. Все необходимые справочные данные (константы) взять из таблиц «Сборника задач по общему курсу физики» под редакцией В.С.Волькенштейн или из приложения к пособию.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1.Тело вращается вокруг неподвижной оси по закону 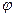=A+Bt+Ct², где А = 10рад, В = 20рад/с, С = -2рад/с². Найти полное уско­рение точки, находящейся на расстоянии r = 0,1м от оси вращения, для момента времени t = 4с.

полное ускорение а точки, движущейся по кривой линии, может быть найдено как гео­метрическая сумма тан­генциального ускорения а_n, направленного к цен­ тру кривизны

траектории (см. рисунок 1).

, т.к. , то

. Тангенциальное и нормальное ускорения точек вращающегося тела выражаются формулами:

; ,

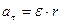где - угловая скорость тела; - его угловое ускорение.

Тогда

Угловую скорость найдем, взяв первую производную от угла поворота по времени:

В момент времени t = 4с угловая скорость

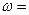[20+2(-2)4] рад/с = 4 рад/с.

Угловое ускорение найдем, взяв первую производную от угловой скорости по времени:

= 2С = -4рад/ с².

Угловое ускорение не зависит от времени, т.е. постоянно. Подстав­ляя найденные значения и исходные данные, получим: = 1.65м/с².

Ответ: а = 1.65м/с².

Пример2. Баллон содержит m₁= 80 г кислорода и m₂ = 320г аргона. Дав­ление смеси Р = 1 МПа, температура Т = 300 К. Принимая данные газа за идеальные, определить емкость баллона.

Решение:

По закону Дальтона, давление смеси равно cумме парциальных давлений газов, входящих в состав смеси.

По уравнению Менделеева-Клапейрона, парциальные давления кислорода Р₁ и аргона Р₂ выража­ется формулами:

Р₁= (m₁ / 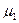)(RT/V); P₂= (m₂ / ) (RT/V).

Следовательно, по закону Дальтона, давление смеси газов

Р= Р₁+Р₂ или Р = (m₁ / 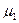+ m₂ / )(RT/V). Откуда ёмкость баллона

V= (m₁ / 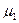+ m₂ / )(RT/Р), где R= 8,31 Дж/(моль К)

V = [(0,08/( 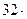10^-3) + 0,32/(40 )) 8,31 /10⁶) = 0,0262 м³

Проверка размерностей:

Ответ: V = 0,0262 м³

Пример3. Конденсатор емкостью С₁ = 3 мкФ был заряжен до разности по­тенциалов U₁ = 40 В. После отключения от источника тока конденсатор был соединен параллельно с другим незаряженным конденсатором емко­стью С₂ = 5 мкФ. Какая энергия израсходуется на образование искры в мо­мент присоединения второго конденсатора?

Решение:

Энергия W¹, израсходованная на образование искры, W¹=W₁-W₂, где W₁-энергия, которой обла­дал первый конденсатор до присоединения к нему второго конденсатора; W₂ - энергия, которую имеет батарея, составленная из первого и второго конден­саторов.

Энергия заряженного конденсатора определяется по формуле

W = CU²/2, где С - емкость конденсатора или батареи конденсаторов; U - разность потенциалов на обкладках

конденсаторов.

Тогда

W¹= C₁U₁²/2 - (C₁+C₂)U₂²/2, где C₁и С₂ - емкости первого и второго конденсаторов; U₁ - разность потенциалов, до которой был заряжен первый конденсатор; U₂ - разность потенциалов на зажимах батареи конденсаторов.

Учитывая, что заряд после присоединения второго конденсатора ос­тался прежний, выразим U₂:

U₂ = q/(C₁+C₂) = C₁U₁/(C₁+C₂).

Тогда

W¹=C₁U₁²/2 - ((С₁+С₂) С₁²U₁²)/(2(C₁+C₂)²)=1/2(C₁C₂/(C₁+C₂))U₁²

W¹=1/2(3 Дж.

[W¹] = (ФФ/Ф)В² = Дж.

Ответ: W¹= Дж.