Расширенная матрица СЛАУ. Элементарные преобразования расширенной матрицы СЛАУ.

Расширенная матрица СЛАУ:

[A_B] – расширенная матрица-система

А=       X=      B=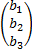

А_В =

Элементарные преобразования расширенной матрицы СЛАУ:

1 – перемены местами любых столбцов матрицы А и любых строк расширенной матрицы А_В всегда допустимо.

2 – можно удалять нулевые строки, одну из одинаковых строк, и строки, элементы которых пропорциональны.

3 – любую строку расширенной матрицы А_В можно умножить на отличное от 0 число.

4 – допустимо прибавлять к элементам строки элементы другой строки, умноженные на произвольное число.

Вопрос №11
Метод Гаусса для решения СЛАУ.

Метод Гаусса – метод последовательного исключения переменных, заключающийся в том, что с помощью элементарных преобразований система приводится к ступенчатому виду, из которой по порядку, начиная с самого последнего номера, находятся все переменные.

При решении системы методом Гаусса выполняется прямой и обратный ход, а затем следует проверка:

1) При прямом ходе: расширенная матрица-система приводится к ступенчатому виду;

2) При обратном ходе последовательно находятся переменные;

3) Проверка.

Вопрос №12

Ранг матрицы. Теорема Кронекера-Капелли.

Ранг матрицы:

Рангом произвольной матрицы А, приведенной к каноническому виду, называется минимальное число из не нулевых строк или столбцов.

Rang A = min(m,n)

где m – кол-во ненулевых строк, n – кол-во ненулевых столбцов.

Теорема Кронекера-Капелли:

Система уравнений является совместной тогда и только тогда, когда ранг расширенной матрицы А_В равен рангу матрицы А.

Rang A_B = Rang A

1. Если ранг матрицы А (Rang A) = числу совместных неизвестных переменных, то система определенная

2. Если Rang A < n(n – кол-во неизвестных), то система неопределенная.

Вопрос №13

Геометрический вектор. Нулевой и противоположный векторы. Модуль вектора. Коллинеарные и компланарные вектора.

Вектор имеет направление и характеризуется длинной, которая называется модулем.

Геометрический вектор – направленный отрезок.

Если длина вектора =0, то он называется нулевым. Его направление можно считать произвольным.

Вектор «–а» можно считать противоположным вектором для вектора «а», если он имеет такую же длину, но противоположное направление.

Модуль – длина вектора.

Если 2 вектора лежат на 1 прямой или на параллельных прямых, то они называются коллинеарными.

Вектора называются компланарными, если они лежат на 1 плоскости или на параллельных плоскостях.

Вопрос №14