Краткие теоретические сведения. Постановка задачи: найти корни уравнения F(x)=0 на промежутке [хнач

Постановка задачи: найти корни уравнения F(x)=0 на промежутке [х_нач, х_кон] методом простых итераций с заданной точностью ε=0,0001. Предварительное отделение корней уравнения произвести путем табулирования функции F(x) на заданном промежутке с шагом, равным 1/20 от длины промежутка.

Существует несколько различных методов численного решения трансцендентных уравнений, но все они предполагают выполнение двух этапов: первый из них называется "отделение корней", второй - "уточнение корней".

На этапе отделения корней определяются те интервалы заданного промежутка [х_нач, х_кон], в каждом из которых расположен один и только один корень уравнения F(x)=0. Отделение корней можно выполнить путем разбиения промежутка [х_нач, х_кон] на некоторое количество частей с шагом h, вычисления функции F(x) в точках разбиения и выбора таких промежутков разбиения, на концах которых функция F(x) принимает значения разных знаков.

На этапе уточнения корней постановка задачи выглядит так: найти корень уравнения F(x)=0, содержащийся внутри интервала (А, В) с заданной точностью ε. Предполагается, что границы интервала (А, В) найдены на этапе отделения корней.

Для уточнения корней методом простых итерации необходимо исходное уравнение F(x)=0 преобразовать к эквивалентному уравнению x = φ(х). Тогда вычислительный процесс метода простых итераций выглядит так:

- выбираем начальное приближение x₀ как любую точку интервала (А, В);

- вычисляем значение φ(х₀) и называем его x₁, т.е. x₁ = φ(х₀);

- вычисляем значение φ(х₁) и называем его x₂, т.е. x₂ = φ(х₁);

Повторяя эту процедуру, будем иметь в общем виде на некотором k-м шаге:

x_k = φ (x_k-1).

При выполнении условия сходимости <1 последовательность х₀,x₁,x₂,…x_k, … приближается к искомому корню.

Критерием окончания вычислительного процесса является выполнение неравенства ½x_k - x_k-1½< ε.

Сходимость метода простых итераций обеспечивается должным выбором преобразования уравнения F(x)=0 к виду x = φ(х). Существует более или менее универсальный способ преобразования:

т.е. φ(х) выбирается в виде φ(х) = C ^. F(x) + x, а константа С определяется из условия сходимости метода.

Рассмотрим в общем виде процесс определения константы С. Если функция φ(х)=C^.F(x)+x, то условие сходимости метода простых итераций 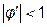выглядит так: 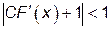. Так как это неравенство содержит знак модуля, то оно распадается на два неравенства:

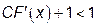и

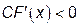или

и

При получаем . При получаем .

Окончательное значение С выбирается как середина найденного интервала или .

Более подробную информацию о методе простых итераций и вопросах его сходимости, а также о других методах численного решения алгебраических уравнений можно найти в [1,3].

Задание

Изучить теоретический материал: постановка задачи, отделение корней, методы дихотомии, хорд, методы Ньютона (касательных, секущих), метод простых итераций.

Найти корни алгебраического уравнения F(x)=0 на промежутке [х_н,х_к] методом простых итераций. Предварительное отделение корней уравнения произвести путем табулирования функции F(x) на заданном промежутке с шагом, равным 1/20 от длины промежутка.

Уравнение и промежуток поиска корней выбрать из таблицы в соответствии с номером варианта.

Для защиты контрольной работы представить на компьютере EXCEL-файл решения задачи и рукописный отчет. В отчете по задаче 1 представить:

- результат отделения корней – значения А, В и соответствующие значения функции F(А), F(В);

- преобразование исходного уравнения к виду x=СF(x)+x с определением значения константы С из условия сходимости метода;

- значение корня уравнения и количество итераций для его достижения для значений точности ε=0,0001;

- ответы на контрольные вопросы.

Пример решения задачи

Порядок решения задачи в среде EXCEL поясним на примере уравнения

ln x – 2 + x = 0

на промежутке [0,5; 7,5].